이번 시간에는 삼각형의 내심의 성질과 위치에 대해 정리해 보았습니다. 내심은 단순히 내접원의 중심이라는 개념을 넘어, 원의 접점, 각의 이등분선, 삼각형의 대칭성을 포함하고 있는 삼각형의 핵심 개념입니다.
이 글에서는 원의 접선과 접점의 성질부터 출발해, 삼각형의 내심의 정의, 성질, 위치까지 체계적으로 정리했습니다. 복잡해 보일 수 있는 내용을 수학적 원리와 논리적 흐름에 따라 하나씩 연결해 나가며, 마치 퍼즐을 맞추듯 개념이 머릿속에서 딱! 하고 맞춰지는 경험을 하실 수 있을 것입니다.
목차
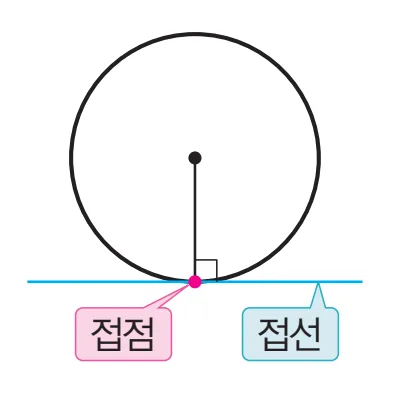
원의 접선과 접점
원과 직선이 한 점에서 만날 때, 이 직선을 원의 접선이라 하고, 그 만나는 점을 접점이라 합니다.
- 직선이 원에 접한다: 원과 직선이 한 점에서 만날 때
- 직선: 원의 접선
- 교점: 접점
접선과 접점 접선의 길이
점과 직선사이의 거리를 중학교 1학년에서 점과 직선사이의 최단거리로 정의하였고, 이 거리는 점과 수선의 발 사이의 거리와 같다고 배웠습니다.
원과 직선이 한 점에서 만날 때 접점은 원의 중심 $O$에서 직선 사이의 최단 거리에 해당하고 따라서 다음이 성립합니다.
- 접점: 원의 중심 $O$에서 접선에 내린 수선의 발
- 접선은 그 접점을 지나는 반지름에 수직이다.
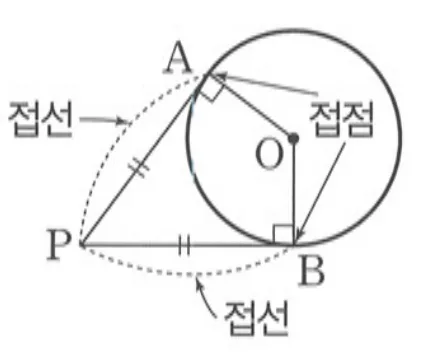
- 원 밖의 한 점에서 그을 수 있는 접선은 2개 이며, 접선의 길이는 같다.
- 보조선 $\overline{PO}$를 그리면 $\triangle{APO} \equiv \triangle{BPO}$ (RHS합동) 이기 때문
다각형의 내접원과 내심 (개념)
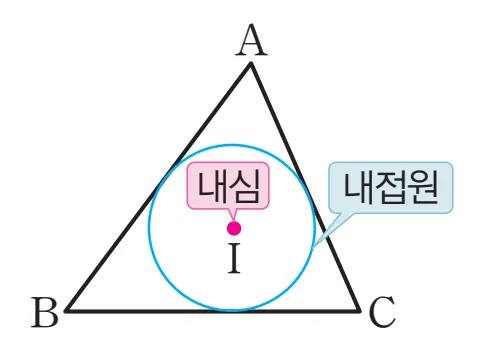
한 다각형의 모든 변이 한 원에 접할 때, 그 원을 다각형의 내접원이라 하고, 그 중심을 내심이라 합니다.
- 다각형의 내접원: 다각형의 모든 변이 접하는 원
- 다각형의 내심: 내접원의 중심
삼각형에서 내심(Inner Center)은 삼각형의 내접원의 중심을 의미하고, 주로 $I$로 나타내고 이를 정리하면 다음과 같습니다.
삼각형의 세 변에 동시에 접하는 원($I$)에 대하여
- 삼각형의 내접원: 세 변에 동시에 접하는 원
- 삼각형의 내심: 내접원의 중심 $I$
삼각형의 내심의 성질
$\triangle{ABC}$의 내심$I$와 내접원과 세 변의 접점$D,\;E,\;F$에 대해 다음이 성립합니다.
- 삼각형의 내심 $I$에서 세 변에 이르는 거리는 같다.
$\overline{ID} = \overline{IE} = \overline{IF}=r$ (내접원의 반지름) - 내심은 세 각의 이등분선의 교점이다.
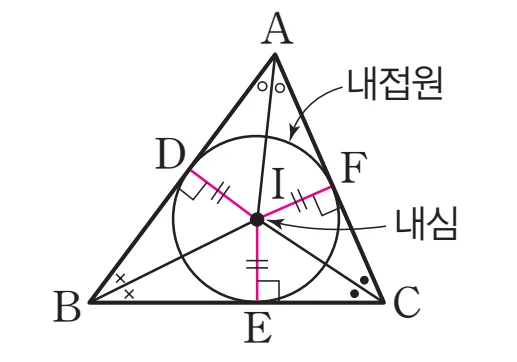
삼각형의 내접원의 중심 $I$가 그림과 같이 주어지면, 세 변에 이르는 거리는 반지름으로 같습니다.
삼각형의 내심 항상 존재?
내심의 성질을 삼각형에 적용하기 전에 내심이 모든 삼각형에 존재하는지 생각해 볼 필요가 있습니다. 만약 항상 존재하지 않고 특수한 상황에만 있다면 성질을 적용할 수 있는 삼각형이 제한 되기 때문입니다. 따라서 아래의 사실을 정리하는 과정이 필요합니다.
- 삼각형의 내심은 항상 존재한다.
삼각형의 내심의 성질(각 변에 이르는 거리가 같다)에서 유추해 보면 삼각형의 내심은 한 내각의 이등분선위에 존재해야 합니다.(각의 이등분선의 조건 참고)
모든 삼각형에서 내심이 존재함을 보이는 것은 아래의 사실을 확인하는 것으로 충분합니다.
- 삼각형의 세 내각의 이등분선은 한 점에서 만난다.
- 삼각형의 두 내각의 이등분선의 교점을 $I$라고 할 때 나머지 내각의 이등분선이 $I$를 지난다.
증명하는 과정은 아래와 같습니다.
[증명]
$\triangle ABC$에서 $\angle A$와 $\angle B$의 이등분선의 교점을 $I$에 대하여
$I$에서 $\overline{AB}, \overline{BC}, \overline{CA}$에 내린 수선의 발을 각각 $D, E, F$라 하면 다음이 성립합니다.
- $\overline{IE} = \overline{IF}$
- $\overline{ID} = \overline{IF}$
따라서 $\overline{IE} = \overline{ID} = \overline{IF}$이고, $I$에서 세 변에 이르는 거리는 같음을 알 수 있습니다.
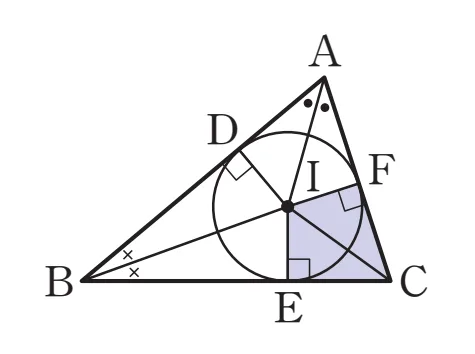
각의 이등분선의 조건에 의해
- $\overline{IE}\bbox[#d0d1e7]{=}\overline{IF}$ $\Rightarrow$ $\angle{ICE} \bbox[#d0d1e7]{=} \angle{ICF}$
따라서 $\triangle{ABC}$의 세 내각의 이등분선은 한 점 $I$에서 만난다고 할 수 있습니다.
삼각형의 내심의 위치
각의 이등분선은 삼각형의 내부에서 교차하게 되고 삼각형의 내심의 위치는 다음과 같이 정리할 수 있습니다.
- 삼각형의 내심은 모든 삼각형에서 항상 내부에 존재한다.
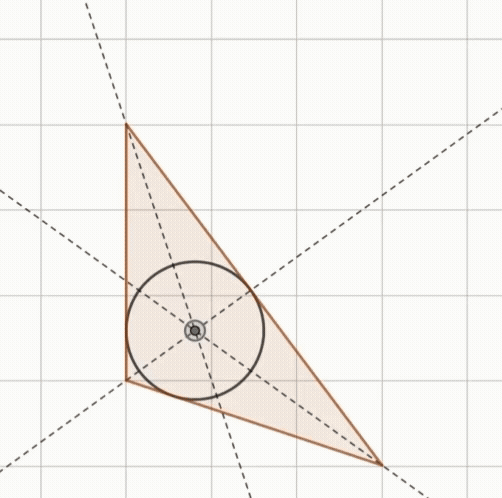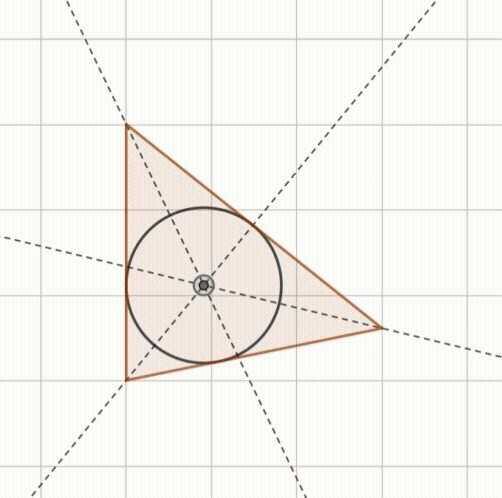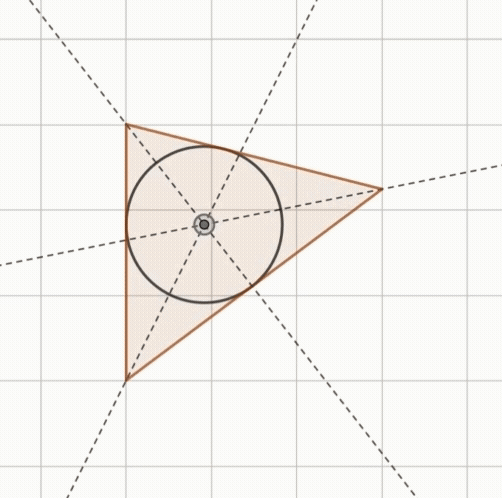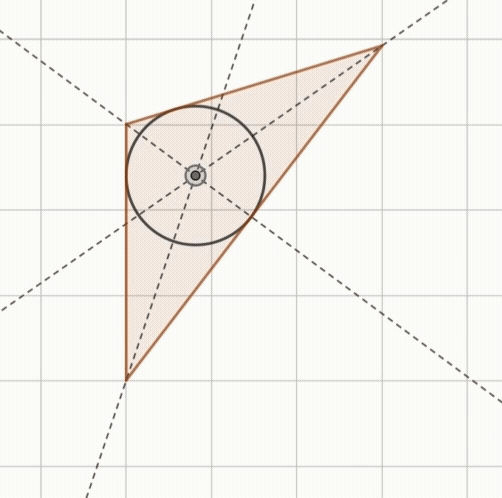
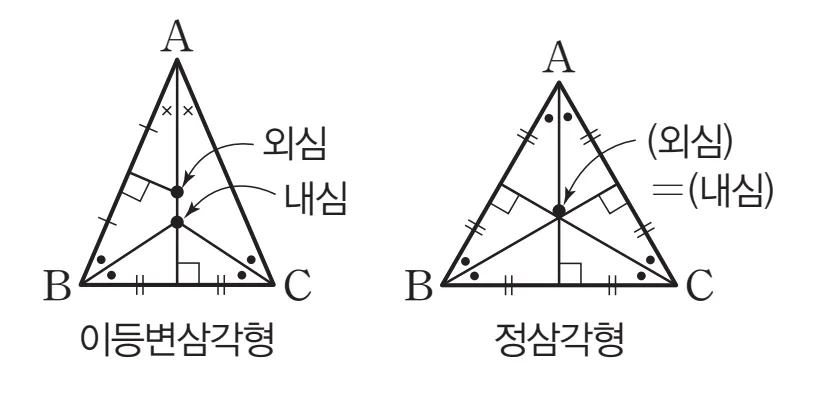
이등변삼각형과 정삼각형의 내심
이등변삼각형
($\overline{BC}$의 수직이등분선)$=$ ($\angle{A}$의 각의 이등분선) 이므로 이등변삼각형의 내심과 외심의 위치는 다음과 같이 정리할 수 있습니다.
- 이등변삼각형은 외심과 내심이 꼭지각의 이등분선(밑변의 수직이등분선) 위에 위치한다.
정삼각형
정삼각형은 각의 이등분선이 대변의 수직이등분선도 되기 때문에 외심과 내심의 위치는 다음과 같이 정리할 수 있습니다.
- 정삼각형은 외심과 내심이 일치한다.
