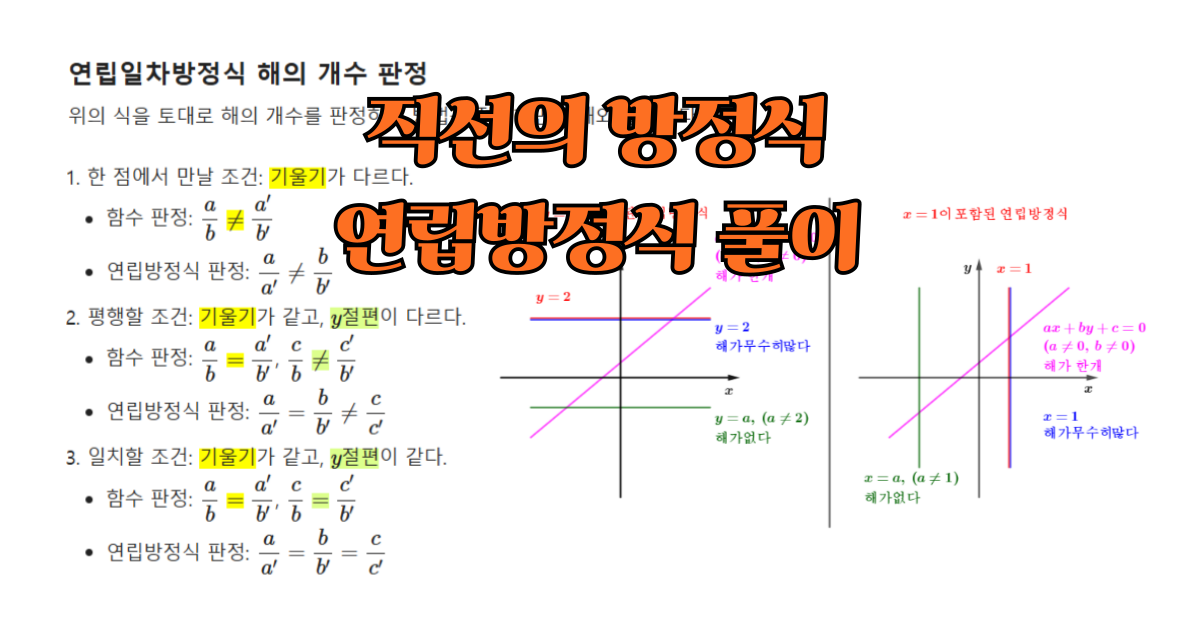
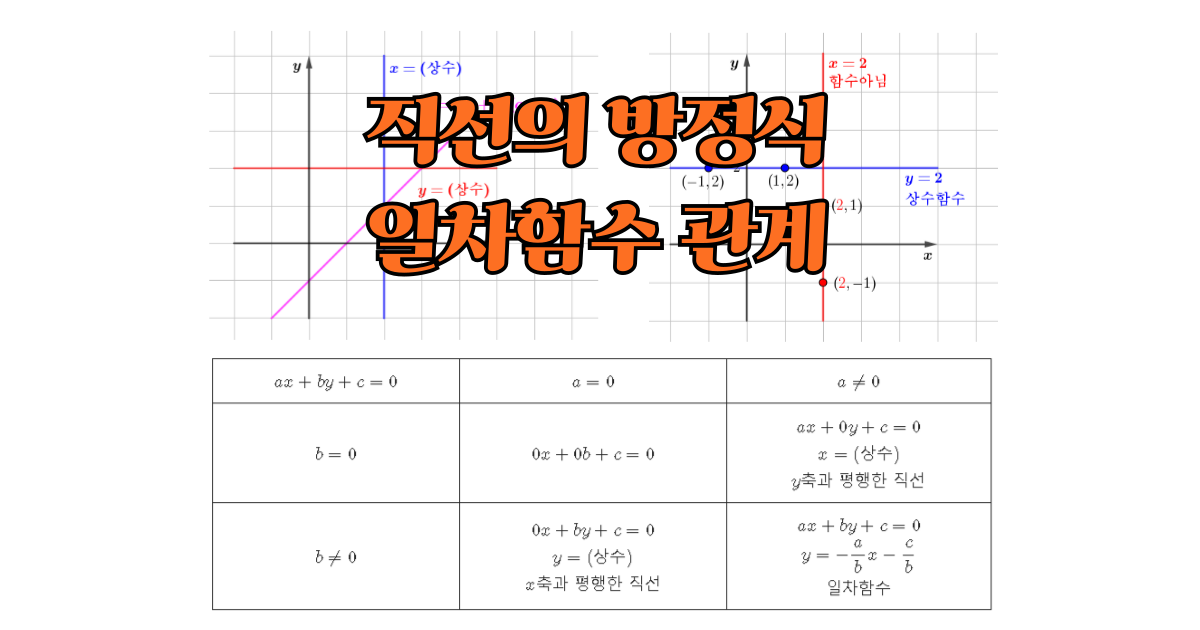
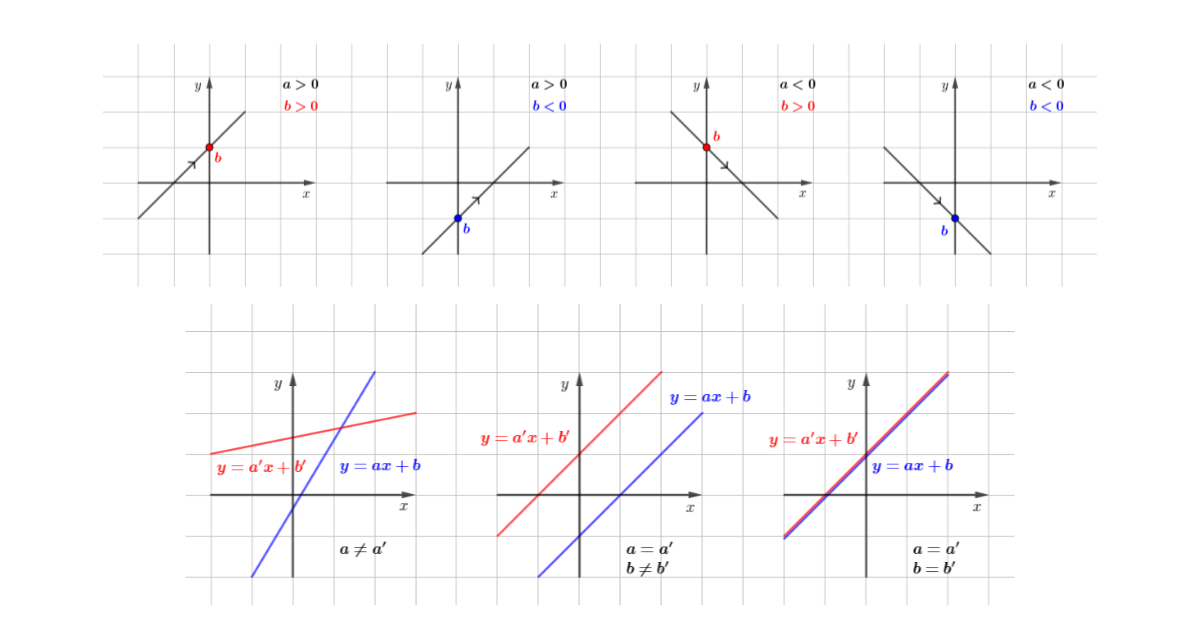
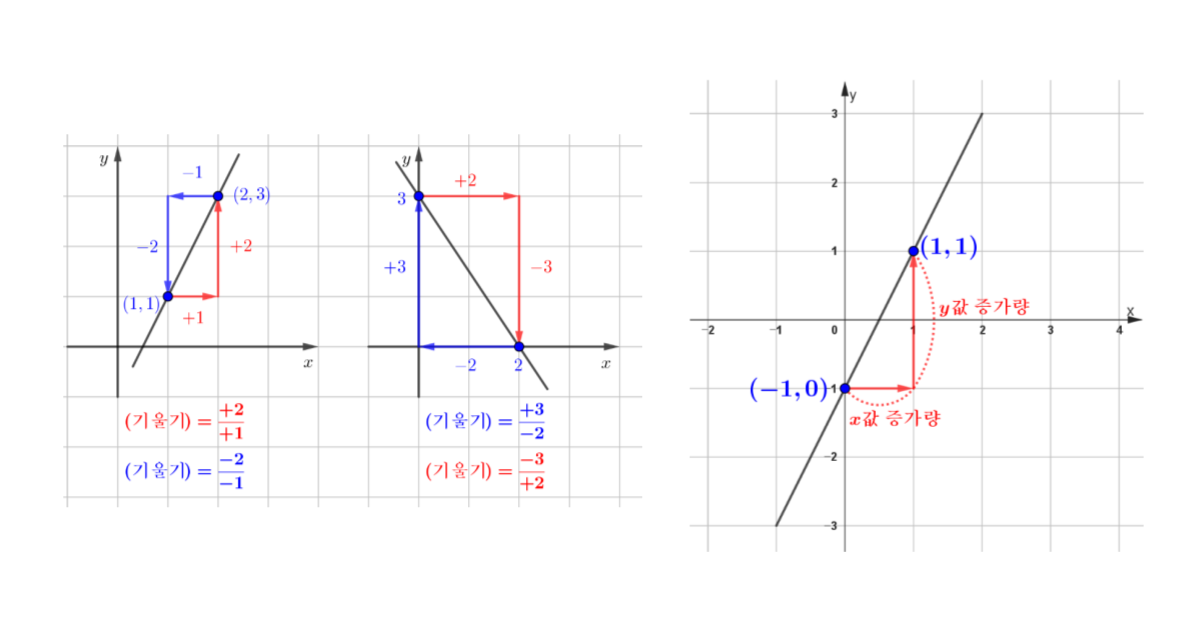
연립일차방정식을 풀 때, 단순히 계산만으로 접근하는 것보다 직선의 방정식으로 이해하면 훨씬 직관적이고 명확합니다. 이 글에서는 연립일차방정식을 두 직선의 교점 문제로 바꾸어 해석하고, 기울기와 y절편을 활용해 해의 개수를 그래프로 판정하는 방법을 자세히 살펴봅니다. 또한, 축에 평행한 직선이 포함된 경우의 예외 상황까지 함께 다루어 헷갈릴 수 있는 개념을 명확히 정리했습니다. 개념을 시각적으로 익히고 싶거나, 연립방정식을 그래프와 연결 … 더 읽기

좌표평면 위의 직선은 모두 일차함수로 표현될까요? 단순히 직선이라면 ‘기울기와 절편’만 알면 충분할 것 같지만, 사실 모든 직선이 일차함수는 아닙니다. 특히 $x$축이나 $y$축과 평행한 직선은 일차함수의 범주를 벗어나기 때문에, 이를 수학적으로 다루기 위해 보다 일반화된 표현, 즉 직선의 방정식이 필요합니다. 이 글에서는 일차함수와 직선의 차이를 직관적으로 이해할 수 있도록 그래프와 표를 활용해 설명하고, 왜 $ax + … 더 읽기

일차함수의 그래프는 단 두 가지 정보 기울기와 절편의 부호 만으로도 개형을 빠르게 예측할 수 있습니다. 이 글에서는 일차함수의 그래프를 어떻게 기울기와 절편을 기준으로 추정할 수 있는지, 그리고 두 일차함수의 위치관계를 어떻게 판정하는지를 직관적으로 설명합니다. $y=ax+b$ 그래프, 기울기, 절편(복습) $y=ax+b$ 그래프 $y=ax+b,\;(a\neq0)$의 그래프는 $y=ax$의 그래프를 위쪽으로 평행이동한 그래프이고, 다음과 같이 학습하였습니다. $y=ax+b$ 기울기와 절편 기울기 절편으로 … 더 읽기

일차함수 $y = ax + b$는 중학교 수학의 핵심 중 하나입니다. 하지만 단순한 공식 외우기로는 그래프를 정확하게 그리기 어렵고, 기울기와 절편이 어떤 의미인지 헷갈리는 경우가 많습니다. 이 글에서는 복습이 필요한 학생들을 위해 기울기, 절편의 의미로부터 관계식 구하기까지 단계별로 정리했습니다. 특히 그래프 그리는 요령과 관계식 구하는 방법을 실전 예시와 함께 설명하였습니다. $y=ax+b$ 그래프, 기울기, 절편(복습) $y=ax+b$ … 더 읽기

중학교 수학에서 가장 기본이면서도 중요한 개념 중 하나는 바로 일차함수입니다. 특히 정비례 관계부터 시작해 그래프를 이해하고, 절편과 기울기의 의미를 정확히 파악하는 것은 앞으로 배우게 될 다양한 함수 개념의 기초가 됩니다. 이 글에서는 정비례 관계를 다시 복습하고, 일차함수의 그래프에서 기울기와 절편이 어떤 의미를 가지며, 어떻게 계산하는지까지 친절하게 설명하엿습니다. 이 글을 통해 일차함수가 훨씬 쉽게 느껴지시길 바랍니다. … 더 읽기

수학에서 ‘함수’는 단순한 계산식이 아니라, 변수 사이의 관계를 이해하는 데 꼭 필요한 개념입니다. 중학교 1학년 때 배운 ‘정비례’를 바탕으로, 변수들이 어떤 방식으로 연결되어 있는지를 함수라는 개념으로 확장해봅시다. 이 글에서는 먼저 정비례 개념을 간단히 복습한 뒤, 함수의 정의와 기본 용어, 그리고 이를 수학적으로 어떻게 기호로 나타내는지를 단계적으로 정리하고, 함수가 왜 중요한지, 어떤 조건에서 함수라고 할 수 … 더 읽기

연립방정식을 풀 때마다 계산하고 가감법을 사용해야 해서 귀찮으셨죠? 사실, 해의 개수는 복잡하게 계산하지 않아도 수식만 보고 바로 답을 알 수 있는 간단한 방법이 있습니다. 이 글에서는 ax=b 꼴 방정식의 성질부터 연립방정식 해 판별 공식까지 모든 과정을 쉽게 정리했습니다. 이 공식을 알면 ‘해가 1개인지, 무수히 많은지, 아니면 아예 없는지’를 순식간에 구분할 수 있어 문제 풀이 속도가 … 더 읽기

연립일차방정식은 두 개 이상의 미지수를 포함하는 두 일차방정식을 동시에 만족하는 해를 구하는 수학적 방법입니다. 특히 대입법과 가감법은 가장 기본적이면서도 강력한 연립방정식 풀이 방법입니다. 하지만 방정식이 복잡하거나 괄호, 분수, 소수 등이 포함되면 학생들이 어려움을 느끼기 쉽습니다.이번 글에서는 대입법과 가감법의 원리를 쉽게 정리하고, 복잡한 연립방정식 문제까지 단계별 풀이 방법을 예시와 함께 자세히 안내합니다. 문제 풀이 흐름을 정확히 … 더 읽기

미지수가 두 개인 일차방정식은 중학교 수학에서 기본이 되는 중요한 단원 중 하나입니다. 두 미지수에 대한 일차식의 구조와 해를 구하는 방법, 그리고 자연수 조건이 있는 경우의 풀이 과정을 예시와 함께 정리하였습니다. 아래 내용을 통해 미지수가 2개인 일차방정식과 연립일차방정식에 대한 개념을 정확히 이해하길 바랍니다. 미지수가 2개인 일차방정식 미지수가 두 개인 일차방정식이란, 미지수가 2개이고 두 미지수에 대한 차수가 … 더 읽기

고등학교 다항식이 복잡하다고 생각되신다면, 아마 중학교 때보다 많아진 문자 때문일 겁니다. 고등학교에서는 여러 문자가 섞인 다항식을 다루면서 용어나 정리 방식도 조금 더 체계적으로 확장됩니다. 이 글을 통해 다항식의 기본 개념부터 다항식을 내림차순, 오름차순으로 정리하는 방법, 다항식의 덧셈과 뺄셈의 원리까지 차근차근 살펴보면서 복잡한 다항식도 쉽게 정리할 수 있는 자신감을 얻어가시길 바랍니다. 다항식 용어확장 다항식의 용어는 다음과 … 더 읽기

비율과 백분율, 그리고 소금물의 농도가 어렵게만 느껴지나요? 수학 시간에 자주 등장하는 개념이지만, 헷갈리는 경우가 많습니다. 비율과 백분율의 차이, 소금물의 농도 문제를 푸는 기본 공식, 그리고 가장 많이 나오는 세 가지 유형까지! 이 글 하나로 헷갈림 없이 개념을 확실히 잡아볼 수 있습니다. 끝까지 이해하면 문제 풀이가 훨씬 쉬워질 것입니다. 비율과 백분율(%) 비율 비율은 어떤수에 대한 다른 … 더 읽기

공부에 집중하기 위해 ‘어떤 의자에 앉느냐’가 매우 중요합니다. 특히 하루 종일 앉아서 공부하거나 업무를 보는 분이라면 착석감과 안정성, 그리고 소음 여부까지 꼼꼼히 따져봐야 하죠. 시험을 준비하는 수험생이나 장시간 앉아 있는 직장인이라면, 허리를 제대로 받쳐주고 흔들림 없이 바른 자세를 유지할 수 있는 의자를 선택하는 것이 집중력 유지에 큰 도움이 됩니다. 이번 글에서는 이런 조건을 모두 갖춘, … 더 읽기