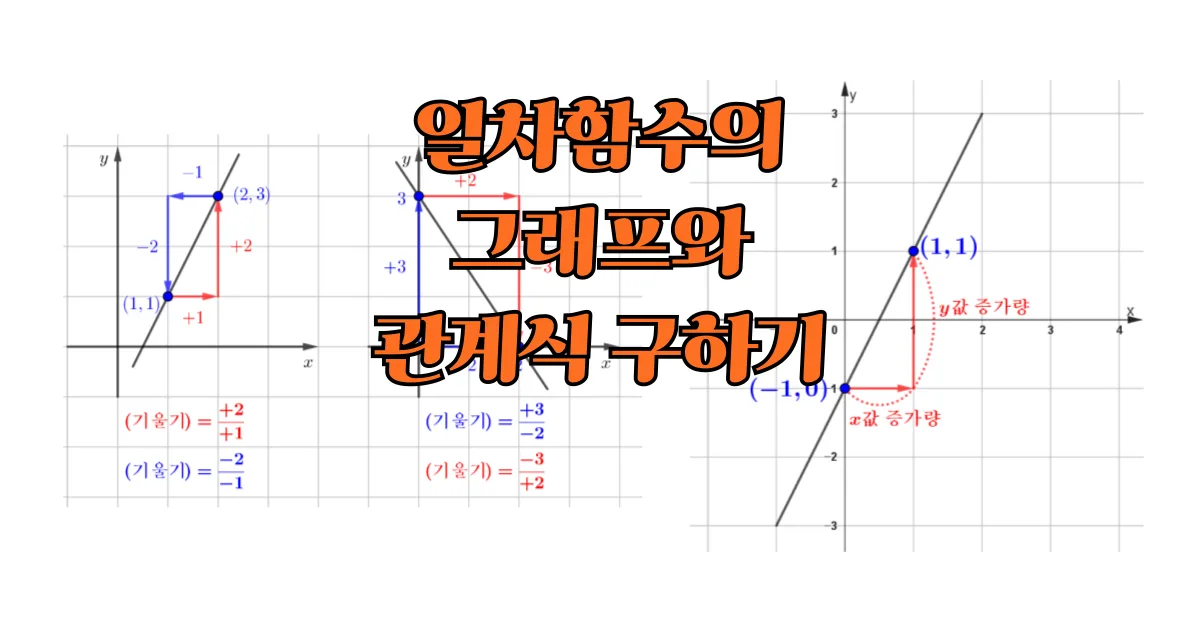
일차함수의 그래프와 관계식 구하기
일차함수 $y = ax + b$는 중학교 수학의 핵심 중 하나입니다. 하지만 단순한 공식 외우기로는 그래프를 정확하게 그리기 어렵고, 기울기와 절편이 어떤 의미인지 헷갈리는 경우가 많습니다. 이 글에서는 복습이 필요한 학생들을 위해 기울기, 절편의 의미로부터 관계식 구하기까지 단계별로 정리했습니다. 특히 그래프 그리는 요령과 관계식 구하는 방법을 실전 예시와 함께 설명하였습니다. $y=ax+b$ 그래프, 기울기, 절편(복습) $y=ax+b$ … 더 읽기