중2 확률 단원에서 처음 배우는 핵심 개념이 바로 ‘경우의 수’입니다. 경우의 수를 제대로 이해하려면 사건의 의미, 합의 법칙과 곱의 법칙, 중복을 처리하는 사고 과정이 함께 정리되어 있어야 합니다.
특히 “중2 경우의 수 계산과 개념”은 이후 중학교 확률, 고등학교 순열, 조합의 기초가 되기 때문에 정확한 개념 정립이 매우 중요합니다.
이 글에서는 경우의 수의 기본 원리부터 합과 곱을 언제 사용하는지(합과 곱의 법칙), 그리고 실전에서 자주 등장하는 중복 처리까지 단계별로 정리하였습니다.
문제를 풀 때 어떤 상황에서 더하고 곱하는지 헷갈렸던 학생과 개념 설명을 찾는 교사 모두에게 도움이 되길 바랍니다.
목차
사건과 경우의 수
일상생활에서 ‘사건’이라고 하면 주로 어떤 특별한 일이나 사고, 또는 한 번 일어나는 일회성으로 발생하는 경우가 많습니다.
- “오늘 교통사고가 일어났다.”, “2026 수능 시험에서 1등급을 맞았다.”
하지만 수학에서의 사건은 전혀 다른 의미를 가집니다. 수학에서는 같은 조건에서 반복할 수 있는 실험이나 관찰에 의해 나타나는 결과를 말합니다. 즉, 동일한 환경 조건에서 여러 번 시도할 수 있고, 그때마다 다른 결과가 나올 수 있는 실험의 가능한 결과가 바로 사건입니다.
- 조건: 반복할 수 있는 실험
- 사건: 반복할 수 있는 실험(조건)이나 관찰에 의하여 나타나는 결과
- 경우의 수: 어떤 사건이 일어나는 가짓수
경우의 수는 빠짐없이, 중복없이 구해야 한다. 이때 순서쌍, 나뭇가지 모양의 그림(수형도)를 이용하면 편리합니다. 다음 예시가 사건에 해당합니다.
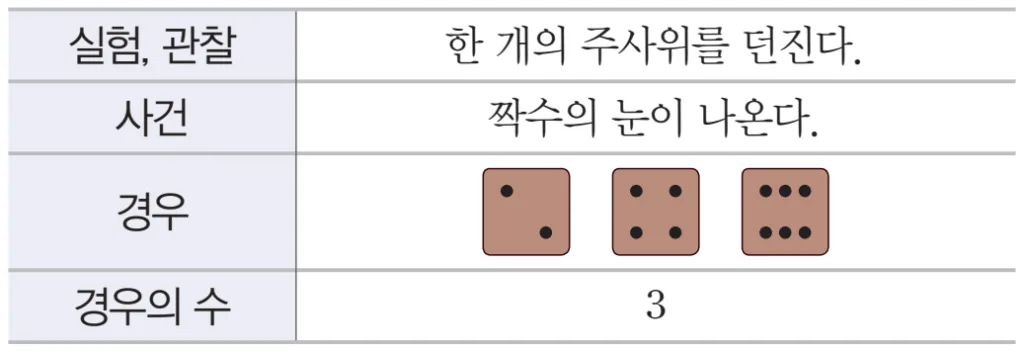
- 조건: 공정한 주사위를 한 번 던진다.
- 사건: 짝수의 눈이 나온다.
- 경우의 수: 3
경우의 수의 합 (합의 법칙)
두 사건 $A, B$가 일어날 경우의 수가 각각 $a,\ b$라고 할 때, 사건 $A$ 또는 사건 $B$가 일어나는 경우의 수는 다음과 같이 계산할 수 있습니다.
- $A,\ B$를 동시에 일어나지 않을 때 : $a+b$ (중3)
- $A,\ B$를 동시에 일날 때(중복: $c$): $a+b-c$ (중3)
포함배제의 원리(고등학교)
두 사건 $A$, $B$가 동시에 일어나지 않는다는 것은 사건 $A$가 일어나면 사건 $B$는 일어나지 않음을 의미합니다.
경우의 수를 생각할 때 다음과 같은 표현이 있을 때 합의 법칙을 적용할 수 있습니다.
- 사건의 설명에서 ‘또는’, ‘~이거나’의 표현이 있으면 두 사건의 경우의 수를 더한다.
예제 1. 한 개의 주사위를 던질 때, 2 이하 또는 4 이상의 눈이 나오는 경우의 수를 구하시오.
풀이
2 이하의 눈이 나오는 경우는 1, 2의 2가지,
4 이상의 눈이 나오는 경우는 4, 5, 6의 3가지이므로
구하는 경우의 수는 합의 법칙에 따라 $2 + 3 = 5$
예제 2. 1~20 까지 숫자가 써진 카드가 들어있는 주머니에서 하나의 카드를 꺼낼 때, 카드가 2의 배수이거나 3의 배수인 경우의 수 (경우의 수 합에서 중복이 발생)
풀이
$2$의 배수: 2, 4, $\bbox[#ffff00]{6}$, 8, 10, $\bbox[#ffff00]{12}$, 14, 16, $\bbox[#ffff00]{18}$, 20
$3$의 배수: 3, $\bbox[#ffff00]{6}$, 9, $\bbox[#ffff00]{12}$, 15, $\bbox[#ffff00]{18}$
$\bbox[#ffff00]{6}$의 배수: $\bbox[#ffff00]{6,\ 12,\ 18}$
(2의 배수 개수)$\bbox[#dcff8d]{+}$(3의 배수 개수)$\bbox[#ffff00]{-}$(중복: 6의 배수 개수)=13
$\bbox[#dcff8d]{\text{포함}} \bbox[#ffff00]{\text{배제}}$
경우의 수의 곱 (곱의 법칙)
두 사건 $A, B$가 일어날 경우의 수가 각각 $n,\ m$일 때사건 $A$, $B$가 동시에 일어나는 경우의 수는 다음과 같이 계산할 수 있습니다.
- 두 사건이 서로 영향을 주지 않을 때: $m \times n$
- 사건 A가 B에 영향을 주면: 영향을 고려해서 경우의 수를 곱한다
경우의 수를 생각할 때 다음과 같은 표현이 있을 때 곱을 적용할 수 있습니다.
- 사건의 설명에서 ‘동시에’, ‘그리고’, ‘~와’, ‘~하고 나서’라는 말이 있으면 두 사건의 경우의 수를 곱한다.
- (서로 다른 동전 $n$개를 동시에 던진다.) = (서로 다른 동전 $n$개를 하나씩 던진다.) = (동전 1개를 $n$번 던진다.)
예제 1. 서로 다른 두 개의 주사위를 동시에 던질 때, 일어나는 모든 경우의 수
풀이
주사위 한 개에는 눈이 1, 2, 3, 4, 5, 6의 6가지가 있으므로
구하는 경우의 수는 $6 \times 6 = 36$
예제 2. 1, 2, 3의 수가 적어진 카드가 하나씩 있을 때, $\square,\ \triangle$ 카드를 두 자리에 배열하는 경우의 수
풀이
$\square$자리를 채우는 경우의 수: 3
$\triangle$자리를 채우는 경우의 수: $(3\bbox[#ffff00]{-1})=2$ ($\bbox[#ffff00]{\text{영향}}$을 고려)
동시에 일어나는 경우의 수 $3\times 2=6$
합과 곱을 이용한 경우의 수
$A$에서 $C$로 가는 길의 경우의 수를 구하는 문제를 통해 곱의 법칙과 합의 법칙을 다시 한 번 적용해 봅시다.
- $A \rightarrow B \rightarrow C$인 경우의 수
- $A \bbox[#ffff00]{\rightarrow} B$, $B \bbox[#dcff8d]{\rightarrow} C$는 서로 영향을 주지않고, 연달아 일어나므로 곱의 법칙을 적용
- $\bbox[#ffff00]{3}\times\bbox[#dcff8d]{2}={\color{blue}6}$
- $A \bbox[#94efef]{\rightarrow} C$와 $A \rightarrow B \rightarrow C$는 동시에 일어날 수 없으므로 두 경우의 수는 합의 법칙을 적용해야 합니다.
- $\bbox[#94efef]{2}+{\color{blue}6}=8$
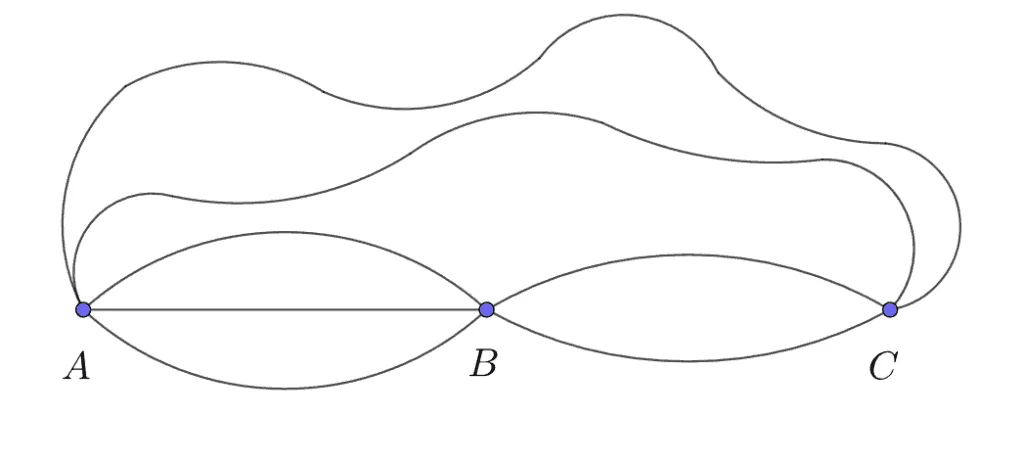
위의 예시를 병렬과 직렬로 이름을 붙이고 다음과 같이 정리하면 문제 상황에 적용이 용이합니다.
- 직렬: $A \xrightarrow[]{n} B \xrightarrow[]{m} C$의 경우의 수
- $n \bbox[#ffff00]{\times} m$
- 병렬: $\begin{cases} A \xrightarrow[]{n} B \xrightarrow[]{m} C \cdots (n \times m)\\A \rightarrow C \cdots (l) \end{cases}$
- $n \bbox[#ffff00]{\times} m \bbox[#dcff8d]{+} l$
경우의 수 계산 총정리 (중복처리)
앞서 정리한 내용을 토대로 경우의 수를 계산하는 과정은 다음과 같습니다.
- $\bbox[#ffff00]{\text{전체 경우의 수}}$ 계산
- 합을 이용(병렬): $\begin{cases} \text{조건} \xrightarrow[]{a} \text{특정사건} \\ \text{조건} \xrightarrow[]{b} \text{특정사건} \end{cases}$
- 경우의 수: $a+b$
- 합에서 $\bbox[#dcff8d]{\text{중복 c가지}}$ 발생: $a+b\bbox[#dcff8d]{-c}$
- 곱을 이용(직렬): $\text{조건} \xrightarrow[]{a} \text{중간사건} \xrightarrow[]{b} \text{특정사건}$
- 경우의 수: $a \times b$
- $b \xrightarrow{\text{a의 영향}} \bbox[#94efef]{b’}$: $a \times \bbox[#94efef]{b’}$
- 합을 이용(병렬): $\begin{cases} \text{조건} \xrightarrow[]{a} \text{특정사건} \\ \text{조건} \xrightarrow[]{b} \text{특정사건} \end{cases}$
- 중복된 경우의 수를 이용: $\bbox[#ffff00]{\text{중복된 경우의 수}} \bbox[#dcff8d]{\div \text{중복횟수}}$
- (사건 $X$의 경우의 수)$=$$\bbox[#ffff00]{\text{전체 경우의 수}}$ $-$(사건 $X$가 일어나지 않을 경우의 수)
전체 경우의 수 중복을 고려하는 상황은 다음과 같습니다.
예제: 5명의 사람이 한 번씩 악수하는 경우의 수
풀이
한 명이 악수하는 경우의 수: $4$ 번
5명이 악수하는 경우의 수: $4+4+4+4+4=20$ 번 (합을 이용)
2명 사이의 악수를 1번만 생각 ($\bbox[#ffff00]{\text{전체 중복}}$): $20\div \bbox[#ffff00]{2}=10$
[출처: 개념원리]
