삼각형의 무게중심과 넓이

삼각형의 무게중심은 단순히 세 중선이 만나는 점이 아닙니다. 무게중심은 중선을 $2:1$로 나누고, 넓이를 일정한 비율로 나누는 중요한 성질을 지니고 있습니다. 본문에서는 중선이 삼각형의 넓이를 6등분하는 이유에 대해 증명하였고, 이를 평행사변형으로 확장하여 정리해 보도록 하겠습니다.

삼각형의 무게중심과 넓이

$\triangle ABC$에서 점 $G$가 무게중심일 때 다음이 성립합니다.

삼각형의 세 중선에 의하여 삼각형의 넓이는 6등분된다.
삼각형의 무게중심과 세 꼭짓점을 이어서 생기는 세 삼각형의 넓이는 같다.

위의 내용은 다음과 같이 표현할 수 있습니다.

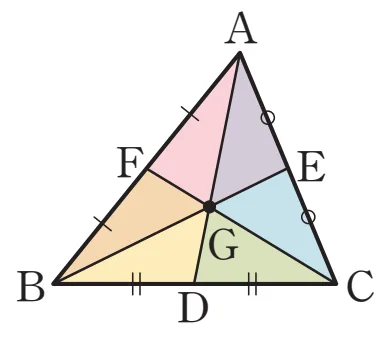
삼각형의 세 중선에 의하여 삼각형의 넓이는 6등분된다.

$\triangle GAF = \triangle GFB = \triangle GBD$$= \triangle GDC = \triangle GCE = \triangle GEA$$= \dfrac{1}{6}\triangle ABC$
6개의 삼각형은 넓이는 같지만 합동은 아니다.

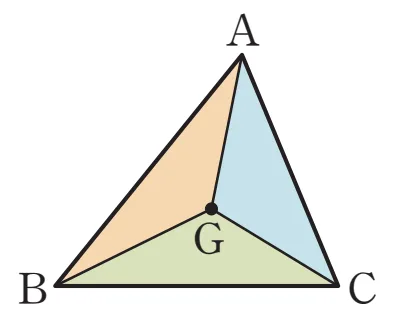
삼각형의 무게중심과 세 꼭짓점을 이어서 생기는 세 삼각형의 넓이는 같다.

$\triangle GAB = \triangle GBC = \triangle GCA = \dfrac{1}{3}\triangle ABC$
3개의 삼각형은 넓이는 같지만 합동은 아니다.

증명

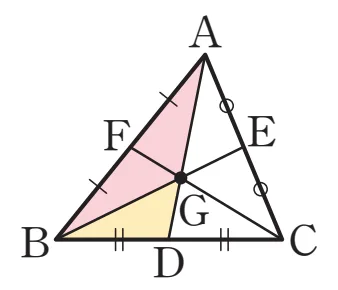
오른쪽 그림의 $\triangle ABC$에서 점 $G$가 무게중심일 때,
$\triangle ABD \bbox[#ffff00]{=} \triangle ADC \bbox[#ffff00]{=} \dfrac{1}{2}\triangle ABC$이고,
$\overline{AG}:\overline{GD} = 2:1$이므로
\begin{flalign} \triangle GBD &= \dfrac{1}{3}\bbox[#ffff00]{\triangle ABD}\\
&= \dfrac{1}{3} \times \bbox[#ffff00]{\dfrac{1}{2}\triangle ABC} = \dfrac{1}{6}\triangle ABC &&\end{flalign}
\begin{flalign} \triangle GAB &= \dfrac{2}{3}\bbox[#ffff00]{\triangle ABD}\\
&= \dfrac{2}{3} \times \bbox[#ffff00]{\dfrac{1}{2}\triangle ABC} = \dfrac{1}{3}\triangle ABC &&\end{flalign}

평행사변형 응용

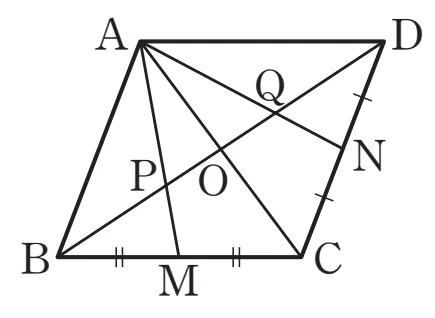
평행사변형 $ABCD$에서 $\overline{BC}$, $\overline{CD}$의 중점을 각각 $M$, $N$이라 하고
$\overline{BD}$와 $\overline{AC}$, $\overline{AM}$, $\overline{AN}$의 교점을 각각 $O$, $P$, $Q$라 하면

점 $P$는 $\triangle ABC$의 무게중심이고, 점 $Q$는 $\triangle ACD$의 무게중심이다.
$\overline{BP}:\overline{PO} = \overline{DQ}:\overline{QO} = 2:1$
$\overline{BP} = \overline{PQ} = \overline{QD} = \dfrac{1}{3}\overline{BD}$
\begin{flalign}\triangle ABP &= \triangle APQ = \triangle AQD \\
&= \dfrac{1}{3}\triangle ABD = \dfrac{1}{6}\square ABCD&&\end{flalign}

증명

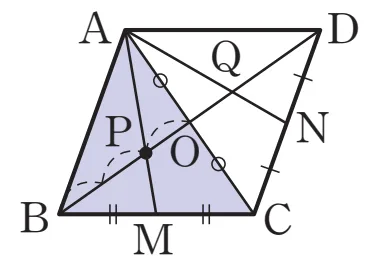
평행사변형의 두 대각선은 서로를 이등분하므로
$\overline{AO} = \overline{CO}$이고 $\triangle ABC$에서 $\overline{AM},\ \overline{BO}$가 중선이다.
따라서 점 $P$는 $\triangle ABC$의 무게중심이고 다음이 성립합니다.

$\overline{BP} : \overline{PO}=2:1$

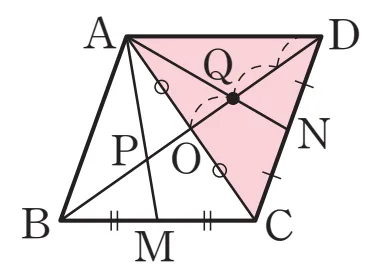
비슷한 방법으로 점 $Q$는 $\triangle ACD$의 무게중심이고 다음이 성립합니다.

$\overline{DQ} : \overline{QO}=2:1$

평행사변형이므로 $\overline{BO} = \overline{DO}$이고 $\overline{BP} : \overline{PO}=\overline{DQ} : \overline{QO}=2:1$ 이므로 다음이 성립합니다.

$\overline{BP}=\overline{PQ} : \overline{QD}=1:1:1$

출처: 개념원리

목차

삼각형의 무게중심과 넓이

평행사변형 응용