사다리꼴과 등변사다리꼴은 중학교 기하 단원에서 자주 다뤄지는 기본 도형이지만, 등변사다리꼴 성질과 조건 사이의 관계는 자세히 다루지 않고 지나가는 학생이 많습니다.
특히 “한 쌍의 대변의 길이가 평행하고 다른 한 쌍의 대변의 길이가 같은 사각형은 등변사다리꼴이다(거짓)”와 같은 거짓 명제는 단순히 진위 여부를 아는 것을 넘어, 조건이 성립하지 않는 반례까지 검토하는 과정이 필요합니다.
이번 글에서는 정의에서 부터 시작해서 사다리꼴과 등변사다리꼴 성질과 성질이 조건이 될 수 있는지를 꼼꼼히 살펴보겠습니다. 끝까지 읽으시면 단순 암기를 넘어 정의, 성질, 조건의 차이를 분명하게 이해하게 될 것입니다.
목차
사다리꼴, 등변사다리꼴 정의
사다리꼴과 등변사다리꼴의 정의는 다음과 같습니다.
- 사다리꼴: 한 쌍의 대변이 서로 평행한 사각형
- $\overline{AD} \pa \overline{BC}$
- 등변사다리꼴: 밑각의 크기가 같은 사다리꼴
- $\overline{AD} \pa \overline{BC}$, $\angle{B}=\angle{C}$
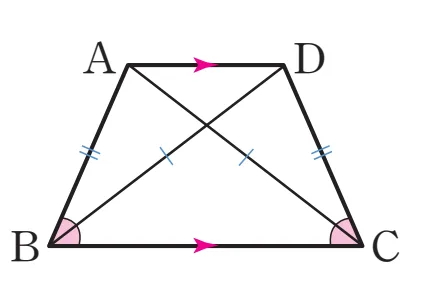
정의를 통해 직사각형이 아닌 평행사변형은 밑각의 크기가 다르므로 등변사다리꼴 아님을 알 수 있습니다.
등변사다리꼴의 성질
등변사다리꼴의 성질을 정리할 때는 다음과 같은 사항을 함께 정리해야 합니다.
- 한 쌍의 대변이 평행하고, 다른 한 쌍의 대변의 길이가 같다. (조건 불가)
$\overline{AB}=\overline{CD}$. - 두 대각선의 길이가 같은 사다리꼴이다. (조건 가능)
$\overline{AC}=\overline{BD}$.
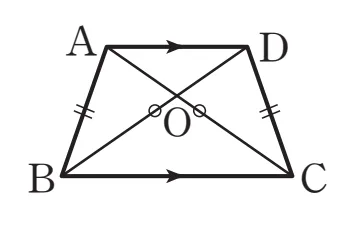
등변사다리꼴은 직사각형을 제외하면 평행사변형이 아니기 때문에, 두 대각선은 서로 다른것을 이등분하지 않음에 주의해야 합니다.
성질1 증명
- 한 쌍의 대변이 평행하고, 다른 한 쌍의 대변의 길이가 같다. (조건은 안됨)
[증명]
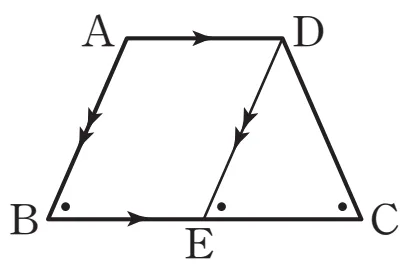
$\overline{AD}\pa \overline{BC}$이고 $\angle{B}=\angle{C}$인 등변사다리꼴 $\square{ABCD}$에 대하여 점 $D$를 지나고 $\overline{AB}$에 평행한 직선을 그어 $\overline{BC}$와 연장선과 만나는 점을 $E$라고 할 때
$\square{ABED}$는 평행사변형이고 다음과 같은 이유로 $\triangle{DEC}$는 이등변삼각형 입니다.
- $\angle{C}=\angle{B}$ (등변사다리꼴)
- $\angle{DEC}=\angle{B}$ (동위각)
따라서 다음이 성립합니다.
- $\triangle{DEC}$ 이등변삼각형: $\overline{DE}=\overline{DC}$
- $\square{ABED}$ 평행사변형: $\overline{AB}=\overline{DE}$
이를 정리하면 $\overline{AB}=\overline{DC}$임을 알 수 있습니다.
오개념 정리
- 한 쌍의 대변이 평행하고 다른 한 쌍의 대변의 길이가 같은 사각형 $\xrightarrow[]{\times}$ 등변사다리꼴
위의 명제가 사실이 아님을 보이기 위해서는 조건을 만족하면서 등변사다리꼴이 아닌 예를 찾으면 됩니다. 이러한 예를 반례라고하고 이 명제의 반례는 평행사변형(직사각형이 아닌)입니다.
어떻게 바꾸면 조건이 될 까?
다음과 같이 바꾸면 조건이 되는 것을 알 수 있습니다.
- 평행하지 않은 한 쌍의 대변의 길이가 같은 사다리꼴은 등변사다리꼴이다.
[증명]
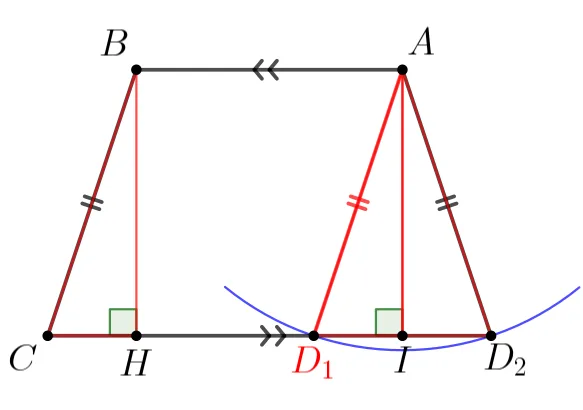
$\overline{AB}\pa\overline{CD}$인 사다리꼴 $\square{ABCD}$에 대하여 $\overline{BC}=\overline{AD}$인 사각형은 $\square{ABCD_1},\ \square{ABCD_2}$가 있습니다.
$\triangle{BCH} \equiv \triangle{AD_1I}$이므로 $\angle{BCH}=\angle{AD_1I}$이고, $\overline{BC} \pa \overline{AD_1}$입니다. 따라서 평행하지 않고 길이가 같은 한 쌍의 대변은 $\overline{BC},\ \overline{AD_2}$ 입니다.
평행하지 않은 한 쌍의 대변의 길이가 같은 사다리꼴 $\square{ABCD_2}$는 다음과 같은 이유로 등변사다리꼴이 됩니다.
- $\angle{BCH}=\angle{AD_2I}$ ($\triangle{BCH} \equiv \triangle{AD_2I}$)
성질2 증명
등변사다리꼴의 두 번째 성질은 아래와 같습니다.
- 두 대각선의 길이가 같은 사다리꼴이다.
[증명]
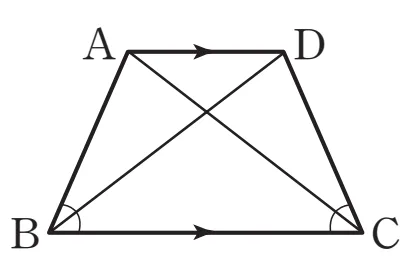
주어진 등변사다리꼴 $\square{ABCD}$의 두 대각선 $\overline{AC}.\ \overline{BD}$에 대하여
$\triangle{ABC} \equiv \triangle{DCB}$ (SAS합동)
- $\angle B=\angle C$ (정의)
- $\overline{BC}$:공통
- $\overline{AB}=\overline{CD}$ (성질1)
따라서 $\overline{AC}=\overline{BD}$입니다.
조건이 될 수 있을까?
위의 성질이 등변사다리꼴의 조건이 될 수 있는지도 생각해 볼 필요가 있습니다.
- 두 대각선의 길이가 같은 사다리꼴 $\Rightarrow$ 등변사다리꼴
[증명]
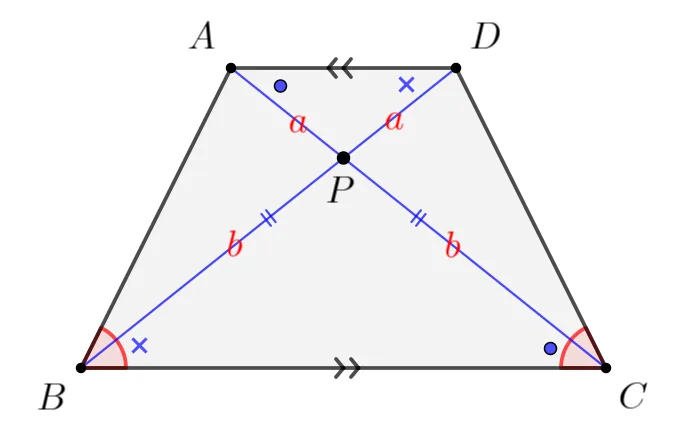
$\overline{AD}\pa \overline{BC}$이고 $\overline{AC}=\overline{BD}$인 사다리꼴 $\square{ABCD}$에 대하여
$\triangle{PAD}\sm\triangle{PCD}$ AA 닮음
- $\angle{PAD}=\angle{PCB}$
- $\angle{PDA}=\angle{PBC}$
닮음비를 $a:b$로 두면 $\overline{PA} : \overline{PC}=\overline{PD} : \overline{PB}=a:b$이고 $\triangle{PBC}$가 이등변삼각형이 됩니다.
위의 사실을 이용하면 $\triangle{DBC}\equiv\triangle{ACB}$ (SAS합동)임을 다음과 같이 보일 수 있습니다.
- $\overline{AC}=\overline{BD}$
- $\overline{BC}$: 공통
- $\angle{DBC}=\angle{ACB}$ ($\triangle{PBC}$:이등변삼각형)
따라서 $\angle{ABC}=\angle{DCB}$이고 따라서 $\square{ABCD}$는 등변사다리꼴이 됩니다.
오개념 주의
더 나아가서 다음의 성질이 조건이 될 수 없는 이유에 대해 생각해볼 필요가 있습니다.
- 두 대각선의 길이가 같은 사각형 $\xrightarrow[]{?}$ 등변사다리꼴
사실임을 보이기 위해서는 증명해야 하고, 거짓임을 보이려면 반례를 제시하면 됩니다. 성립하지 않는 반례는 다음과 같습니다.
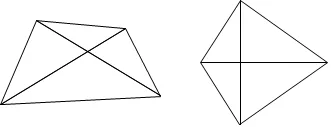
명제의 참과 거짓
$\bbox[#ffff00]{\text{두 대각선의 길이가 같은 사각형}}$ $\rightarrow \bbox[#dcff8d]{\text{등변사다리꼴}}$
위와 같이 $\bbox[#ffff00]{\text{조건}}$과 $\bbox[#dcff8d]{\text{결과}}$로 이루어진 문장을 명제라고 합니다. 주어진 명제가 참인지 거짓인지 보이는 것은 수학에서 중요한 과정입니다. 이러한 과정에서 사용할 수 있는 논리는 아래와 같습니다.
- 명제가 참임을 보이는 방법
- 직접증명: 조건 $\rightarrow \rightarrow \rightarrow$ 결론을 직접 보이는 것
- 간접증명(귀류법): $\bbox[#ffff00]{\text{조건}}\circ$, $\bbox[#dcff8d]{\text{결과}} \times$인 경우는 $\color{red}{\text{모순}}$임을 보이는 것
- 명제가 거짓임을 보이는 방법
- 반례: $\bbox[#ffff00]{\text{조건}}\circ$, $\bbox[#dcff8d]{\text{결과}} \times$
반례는 나중에 배울 귀류법적 사고의 기초가 되기 때문에 중학교 2학년 시기에 반드시 이해하고 넘어가야 합니다.
[이미지출처: 개념원리]
여러가지 사각형에대한 성질은 다음 포스팅을 참고해 주세요.
