회전체 문제 정리 최단거리 (원뿔, 원기둥, 원뿔대)

이번 시간에는 회전체 문제를 유형별로 정리해 보았습니다. 기본적인 문제부터 원뿔과 원뿔대에 숨겨진 비율과, 원뿔과 원기둥의 전개도를 이용한 최단거리 문제를 다루었습니다.

회전체의 단면 문제

회전하기 전 도형 추론 문제

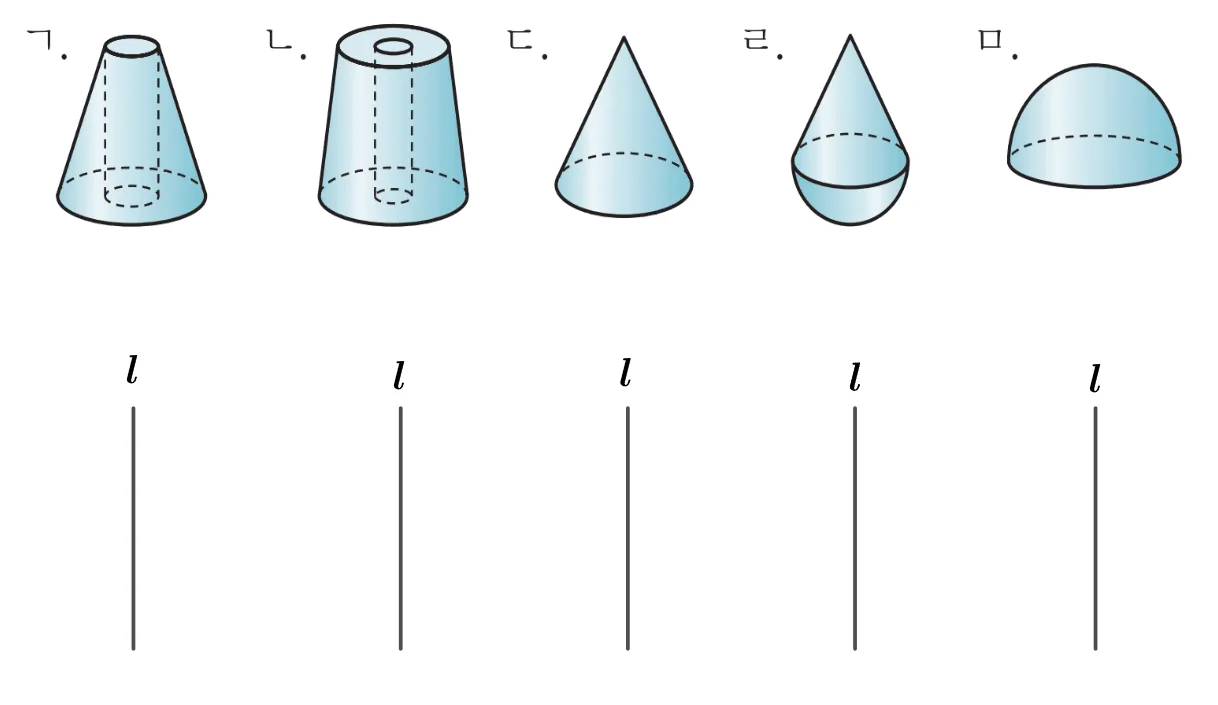
[문제] 평면도형을 직선 $l$을 중심으로 1 회전하여 얻은 회전체에 대하여 회전축과 평면도형을 그림으로 나타내어라.

[풀이]

회전축을 포함하는 평면으로 자른 단면 $\to$ 회전축에 대칭인 두 도형 $\to$ 하나를 회전축 $l$을 중심으로 회전 $\to$ 회전체

따라서 회전하기 전 도형은 다음과 같이 그릴 수 있다.

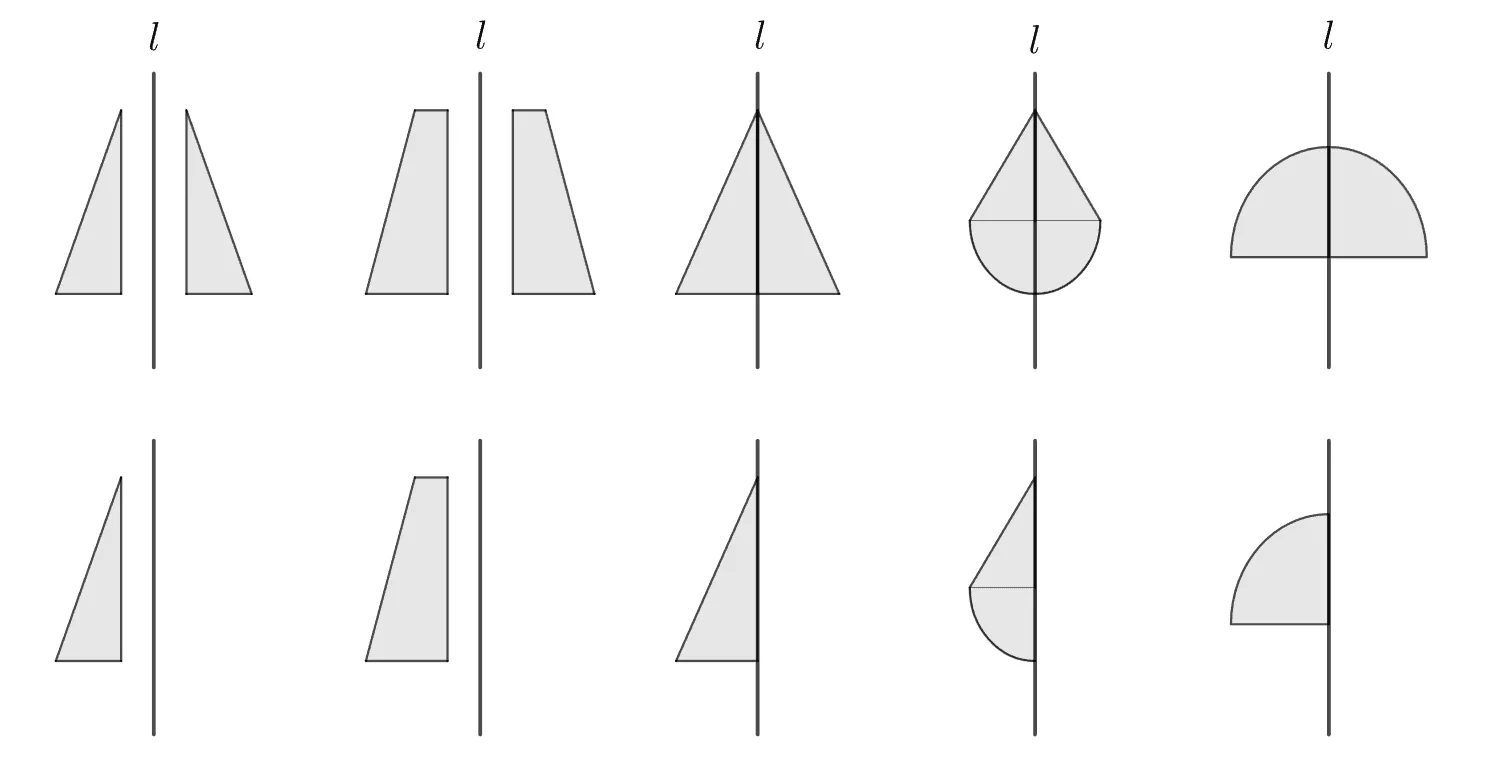
원뿔과 원뿔대의 단면

[문제]

주어진 회전체의 단면에 대하여 다음 물음에 답하여라.

1. 원뿔의 단면으로 적절하지 않은 것을 찾아라.
2. 원뿔대의 단면으로 적절하지 않은 것을 찾아라.

[풀이]

1. 원뿔을 자른 단면이 아닌 것은 4번 사다리 꼴이다.
2. 원뿔대를 자른 단면이 아닌 것은 5번 이등변삼각형이다.

원뿔곡선: 원, 타원, 포물선, 쌍곡선

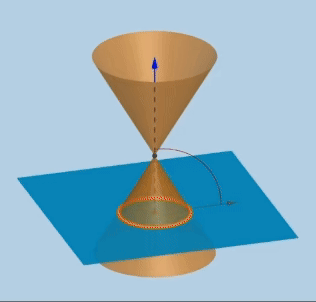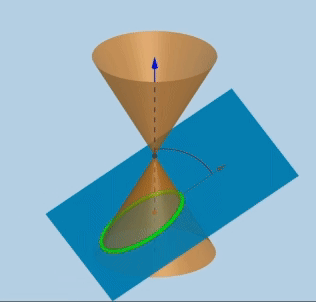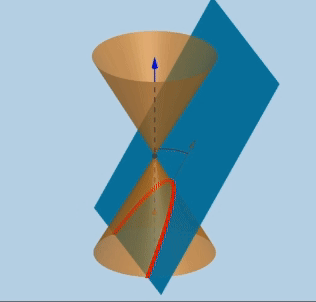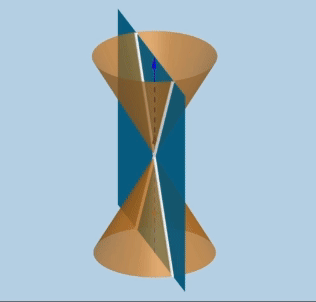
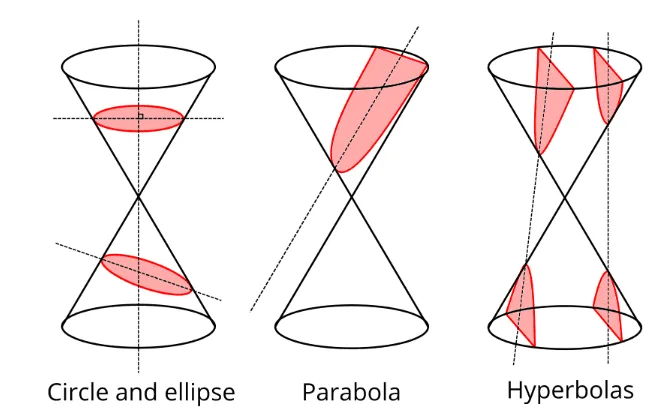
위와 같이 합동인 원뿔을 나란히 쌓고 평면으로 자르면 아래와 같은 도형이 만들어 진다.

• 원(circle) : 회전축과 수직인 평면
• 포물선(parabola) : 모선과 평행인 평면
• 타원(ellipse): 원과 포물선 사이
• 쌍곡선(hyperbolas): 두 원뿔과 동시에 만나는 평면

원뿔의 전개도와 반지름 비율 문제

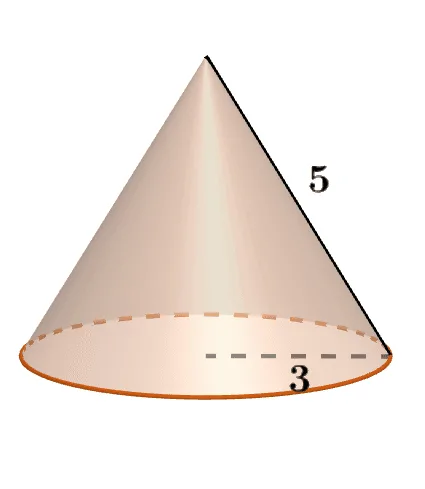
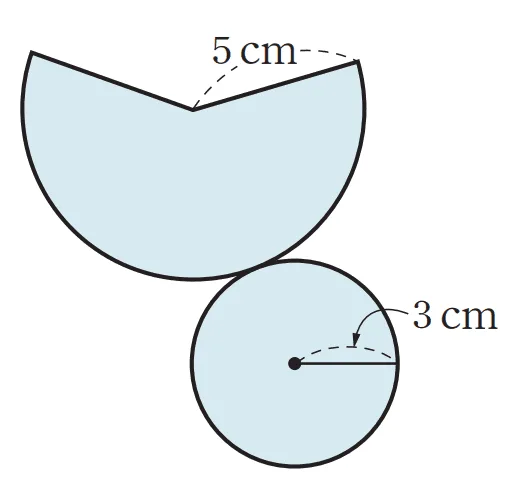
[문제] 모선의 길이가 $5$, 밑면의 반지름이 $3$인 원뿔의 전개도 에서 부채꼴의 중심각 크기를 구하여라.

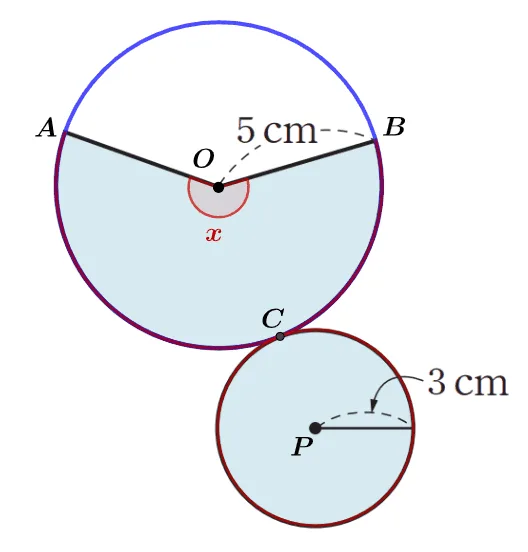
[풀이]

$$\begin{array}{rl}{360}^{\circ }:x^{\circ }& =\text{원 O의 둘레}:\stackrel{⏜}{ACB}\\ & =\text{원 O의 둘레}:\text{원 P의 둘레}\\ & =5:3(\because \text{원의둘레}\propto \text{반지름})\\ \therefore x^{\circ }& ={360}^{\circ }\times {\displaystyle \frac{3}{5}}={216}^{\circ }\end{array}$$

원뿔대 전개도 심화 문제

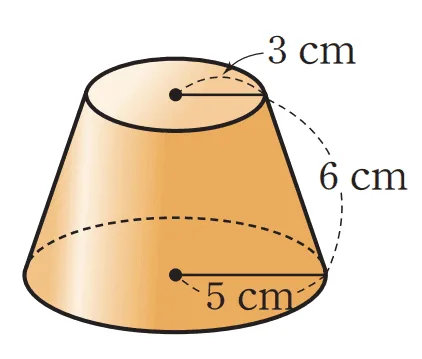
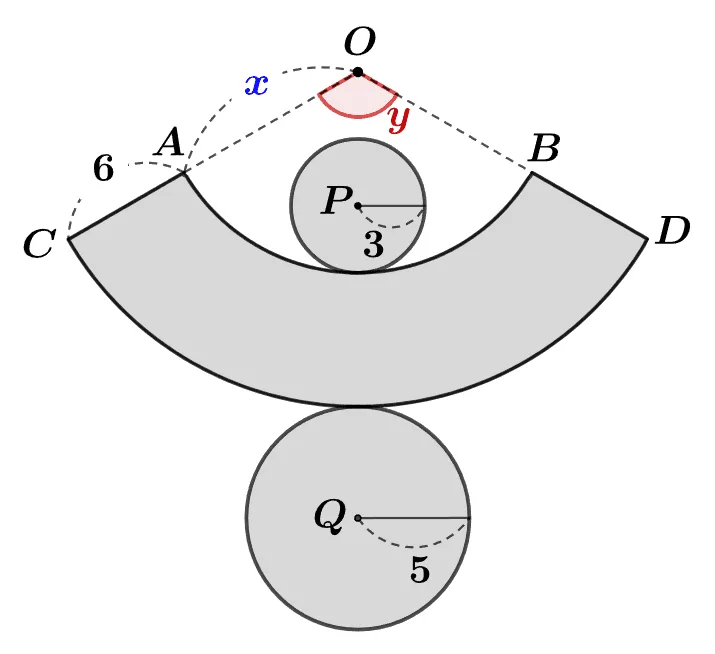
[문제] 주어진 원뿔대의 전개도에 대하여 $x,y$에 적절한 값을 구하여라.

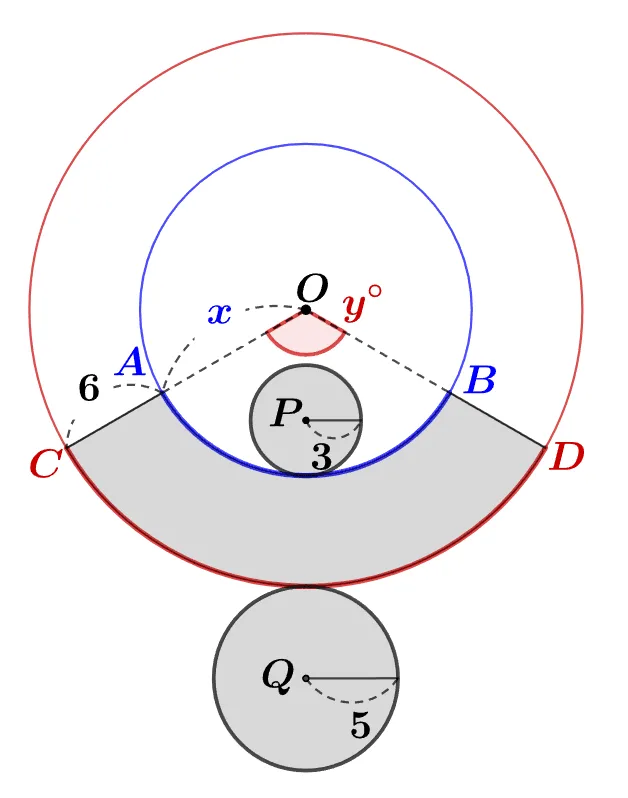
[중학교 1학년 풀이]

중심이 $O$이고 반지름이 $x$인 원의 둘레($l$) 과 $\stackrel{⏜}{AB}$에 대하여

1. ${360}^{\circ }:y^{\circ }=\text{원 O의 둘레}:\stackrel{⏜}{AB}$
2. $\stackrel{⏜}{AB}=\text{원 P의 둘레}$

$$\begin{array}{rl}{360}^{\circ }:y^{\circ }& =\text{원 O의 둘레}:\text{원 P의 둘레}\\ & =x:3\end{array}$$

동일한 논리로 다음이 성립한다.

$$\begin{array}{rl}{360}^{\circ }:y^{\circ }& =\text{원 O의 둘레}:\text{원 Q의 둘레}\\ & =x+6:5\end{array}$$

따라서 $x:3=x+6:5$이고 $x=9$ 이고 ${360}^{\circ }:y^{\circ }=x:3=9:3$ 이므로 $y={12}^{\circ }$이다.

[중학교 2학년 풀이]

부채꼴OAB $\sim$ 부채꼴 OCD 이므로

• $x:x+6=\stackrel{⏜}{AB}:\stackrel{⏜}{CD}$
• $\stackrel{⏜}{AB}:\stackrel{⏜}{CD}=3:5$

따라서 $x:x+6=3:5$ 이고 $x=9$이고,

${\displaystyle \frac{\stackrel{⏜}{AB}}{\text{원 O의 둘레}}}={\displaystyle \frac{6\pi }{18\pi }}={\displaystyle \frac{y^{\circ }}{{360}^{\circ }}}$이므로 $y={120}^{\circ }$이다.

최단거리 문제

원뿔에서 최단거리 문제

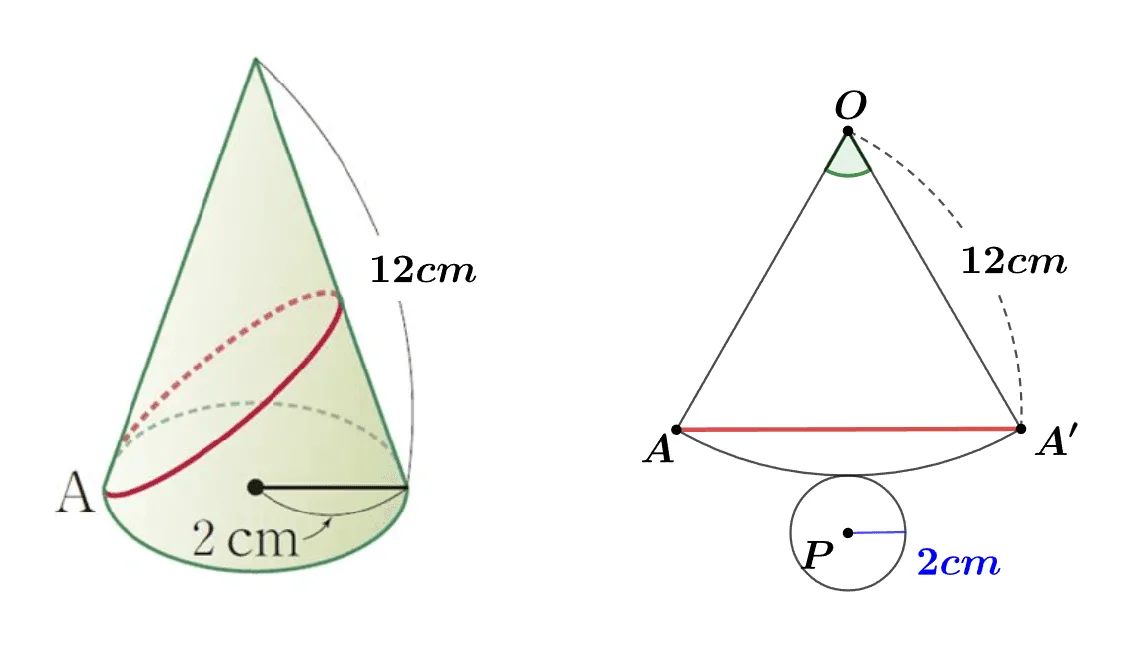
[문제] 모선의 길이 $12cm$, 밑면의 반지름의 길이가 $2cm$인 원뿔에 대하여 밑면의 한 점 $A$에서 출발하여 원뿔 위를 지나 다시 점 A로 돌아오는 최단거리를 구하여라. (입체도형의 겨냥도는 비율을 무시하고 그렸습니다.)

[풀이]

원뿔의 전개도에서 반지름의 비율에 대한 성질을 적용하면 (위쪽 문제 참고) ${360}^{c}irc:\mathrm{\angle }AO{A}^{\prime }=12:2$ 이고 $\mathrm{\angle }AO{A}^{\prime }={60}^{\circ }$이다.

$\mathrm{△}OA{A}^{\prime }$는 정삼각형이고 최단거리는 전개도에서 직선거리($\overline{A{A}^{\prime }}$)를 의미하고$\overline{A{A}^{\prime }}=12cm$이다.

원기둥에서 최단거리 문제

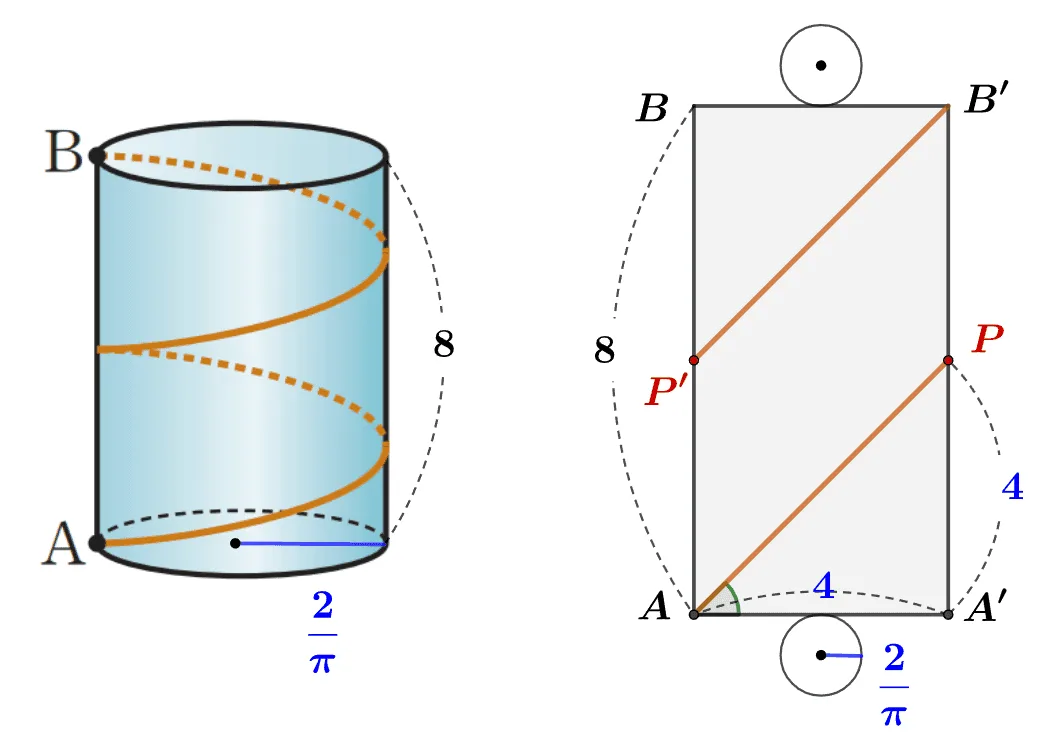
[문제] 밑면의 반지름이 ${\displaystyle \frac{2}{\pi }}$이고, 높이가 $8$인 원기둥에 대하여 서로 다른 두 밑면 위의 점 A, B가 원기둥의 같은 방향에 있을 때 $A$에서 두 바퀴 회전하여 $B$까지 이르는 최단거리를 전개도를 이용해 그리고, 최단거리로 가기위한 지면사이의 각도를 구하여라. (입체도형의 겨냥도는 비율을 무시하고 그렷습니다.)

[풀이]

최단거리는 전개도상에서 직선거리를 의미하므로 그림에 그려보면 위와 같다.

밑면의 둘레는 $2\times {\displaystyle \frac{2}{\pi }}\times \pi =4$이고, $\overline{A^{\prime }P}=4$이므로 최단거리로 가기위해서는 지면에서 ${45}^{\circ }$를 유지하고 회전해야 한다.

이상으로 회전체 문제를 유형별로 정리해 보았습니다.