기출문제는 앞으로의 학습 방향을 잡는 데 있어 가장 중요한 자료입니다. 2025 수능 기출문제 수학 영역을 단순히 풀어보는 것에서 그치지 않고, 출제자의 의도와 풀이 과정을 꼼꼼히 분석해서 2026 수능을 잘 대비하시길 바랍니다.
이번 포스팅에서는 문제와 풀이를 나란히 배치하여 어디서든지 기출문제를 복습할 수 있도록 구성했습니다. 문제를 반복해서 풀어 보면서 문제의 핵심을 잘 파악하는 것이 중요합니다. 기출문제를 통해 수능 수학의 출제 경향을 살피고, 부족한 부분을 채워가며 다가올 수능 시험을 대비해 보세요.
연도별 기출문제는 다음 자료를 이용해 주세요.
목차
2025 수능 기출문제 수학영역
5지선다형

풀이
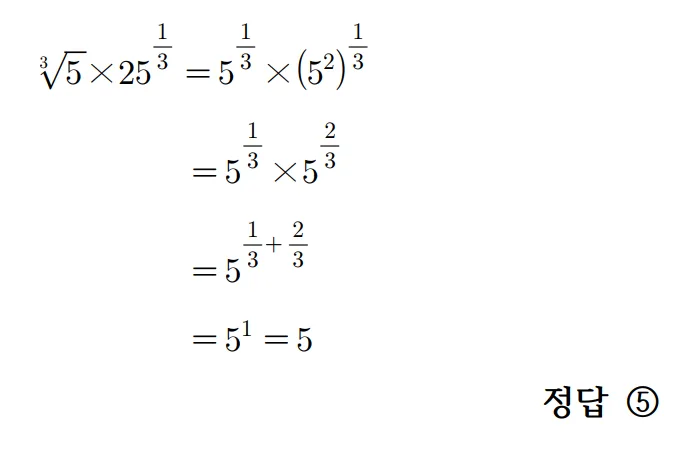

풀이


풀이


풀이


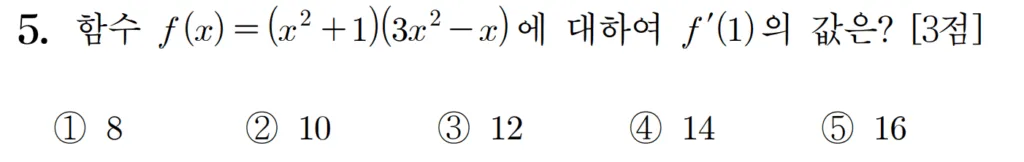
풀이
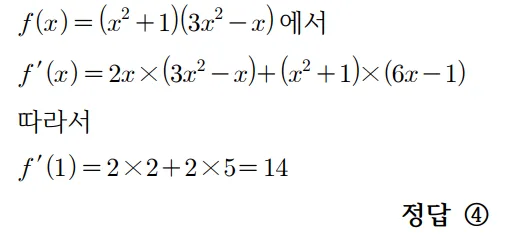
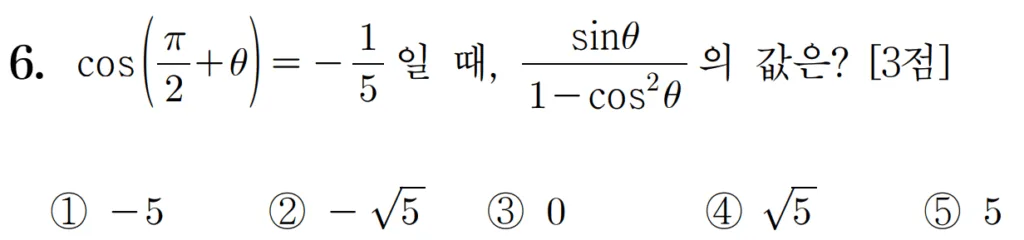
풀이


풀이

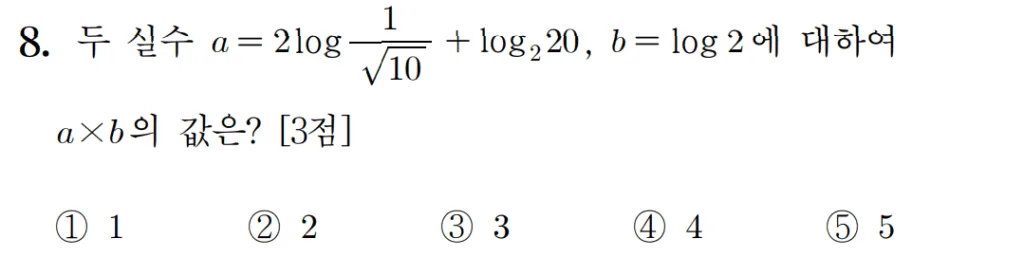
풀이
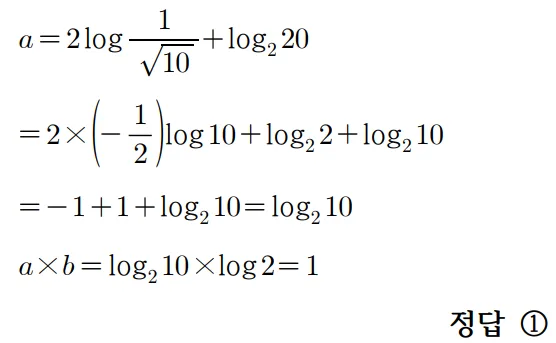
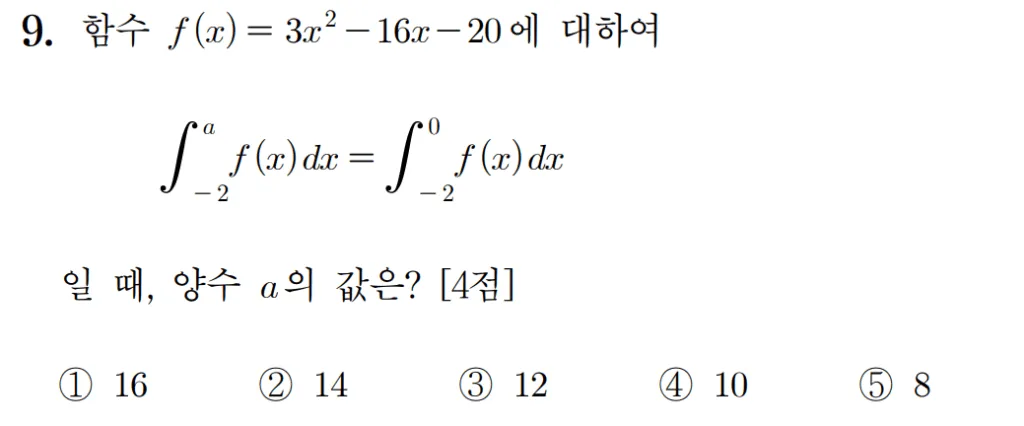
풀이



풀이



풀이


풀이


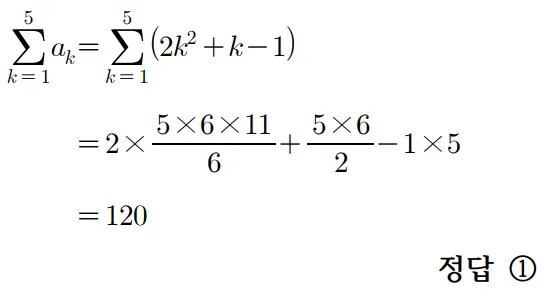
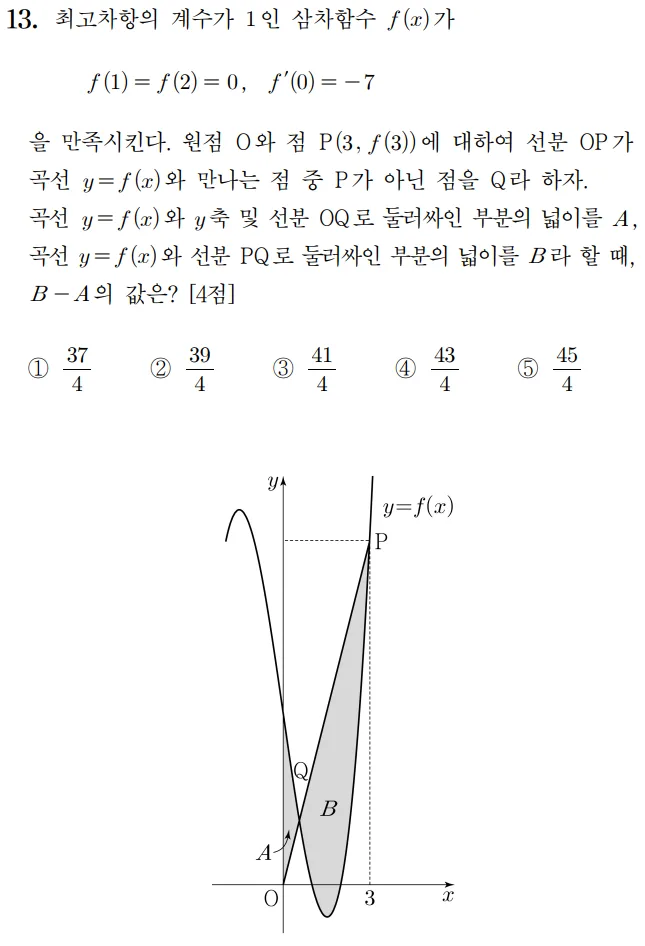
풀이




풀이



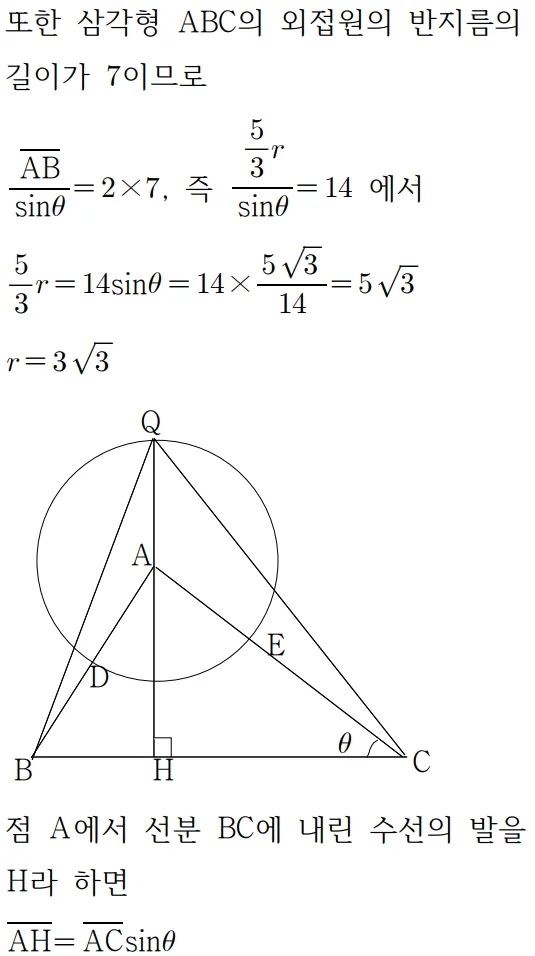


풀이







단답형

풀이
로그의 진수조건에 의해


풀이


풀이
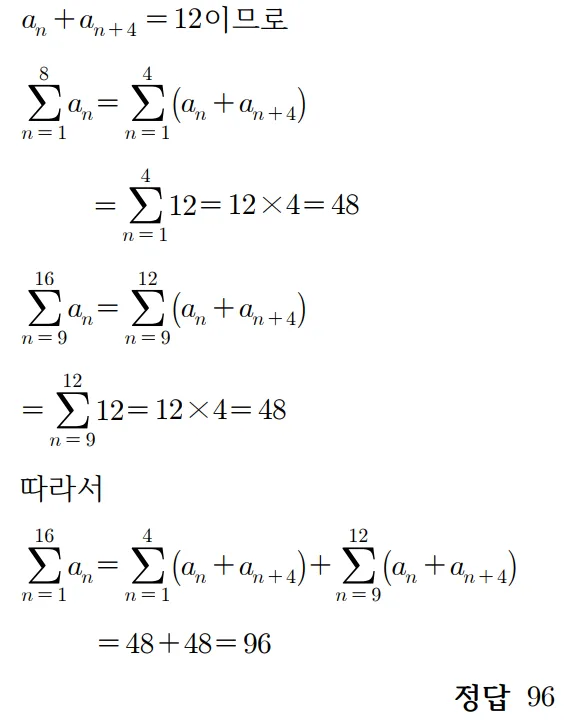

풀이

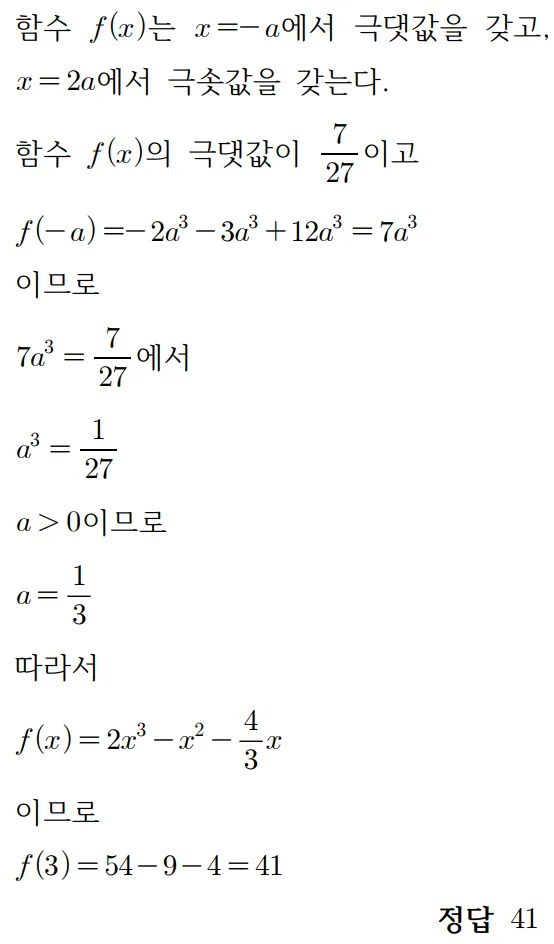

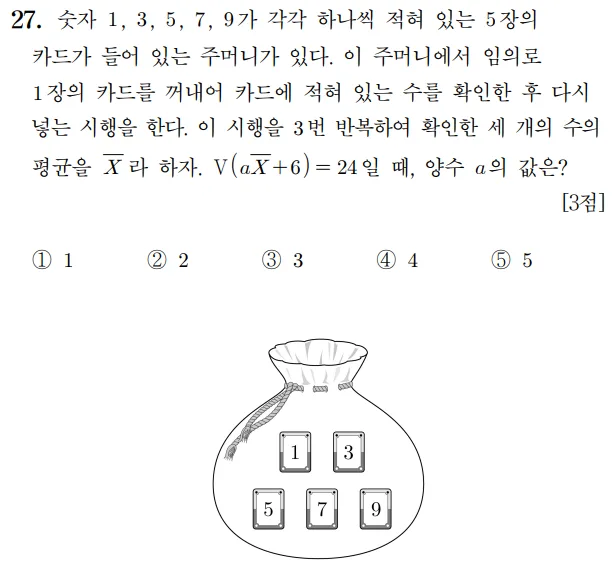
풀이

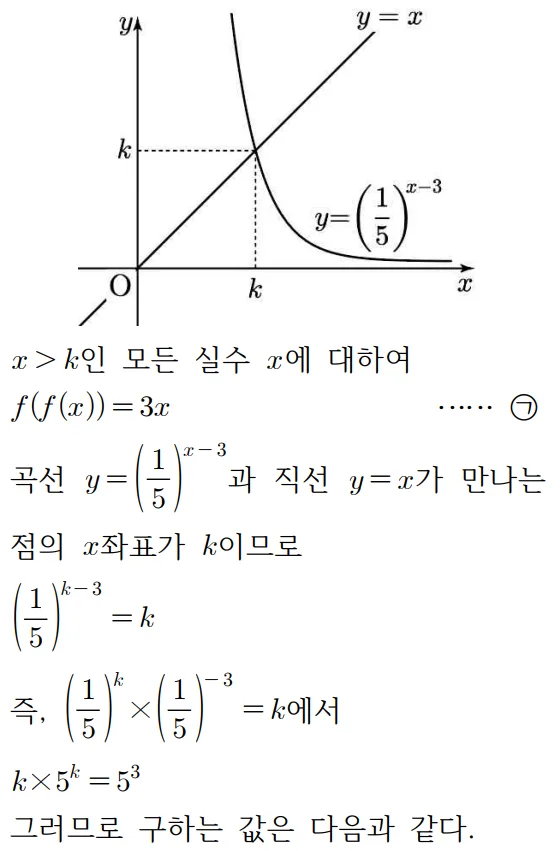


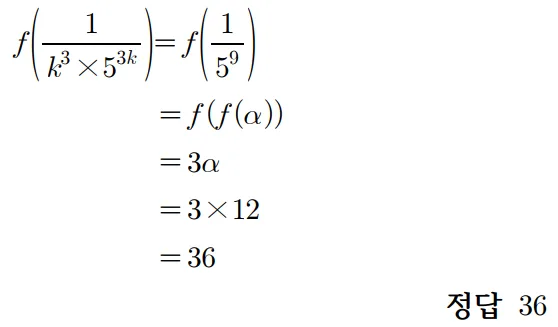

풀이




풀이




선택1. 확률과 통계
5지선다형

풀이


풀이
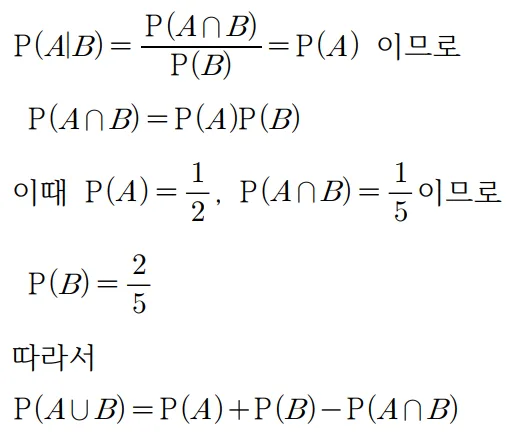
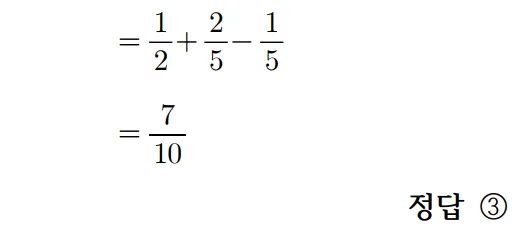

풀이


풀이


풀이

$V(X)=\dfrac{4^2+2^2+0^2+2^2+4^2}{5}=8$


풀이

$2 \leq f(2) \leq f(3) \leq f(4) \leq f(5) \leq 2$
따라서 $2 = f(2) = f(3) = f(4) = f(5) = 2$





단답형형
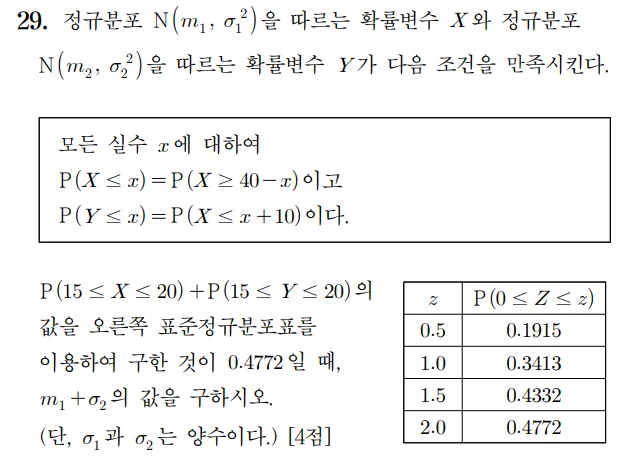
풀이
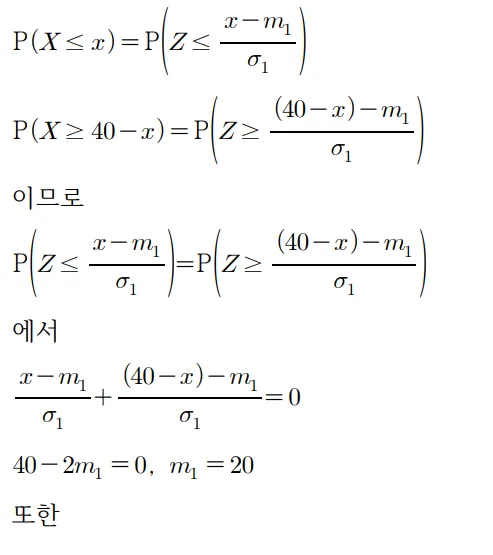


정답 25

풀이




선택2. 미적분
5지선다형

풀이
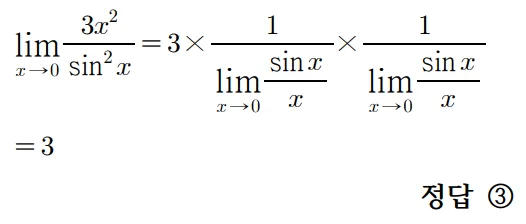

풀이
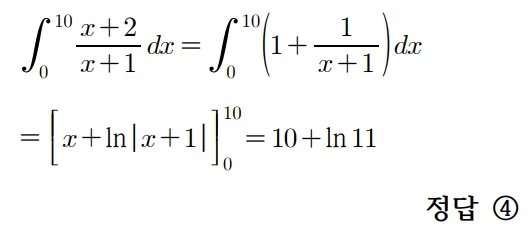
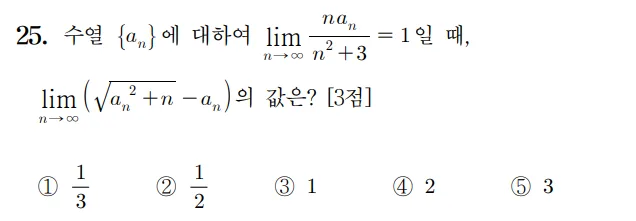
풀이

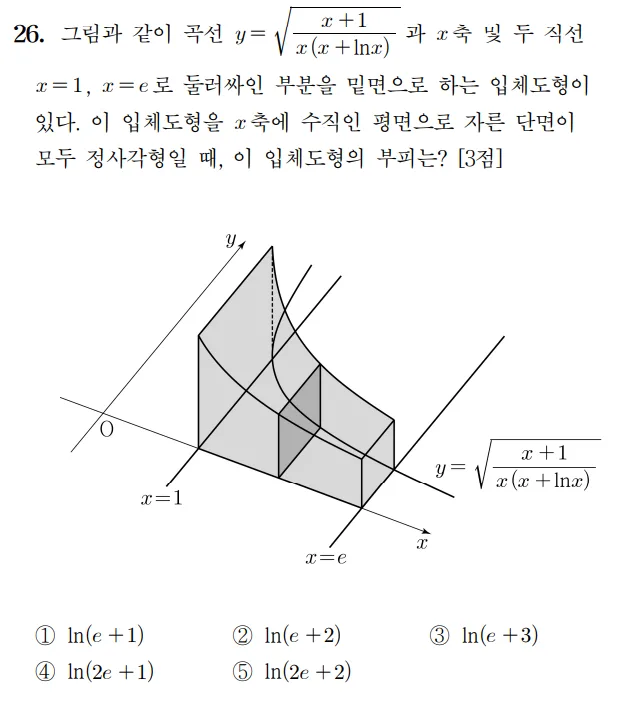
풀이



풀이




풀이

\begin{flalign} g(t) &= \left[ \dfrac{f'(t)}{2}x^2 -tf'(t)+f(t)x \right]_{0}^{t}-\int_{0}^{t} f(x)dx \\
&=\dfrac{1}{2}t^2f'(t) – t^2f'(t) + tf(t)\\
&\quad \quad -\left[ xf(x) +\dfrac{1}{3}x^3+ \dfrac{1}{2} e^{1-x^2} \right]_{0}^{t}\\
&=-\dfrac{1}{2} t^2 f'(t) + tf(t)\\
&\quad \quad – \left( t f(t) + \dfrac{1}{3} t^3 + \dfrac{1}{2} e^{1-t^2} – \dfrac{1}{2} e \right)\\
&=-\dfrac{1}{2} t^2 \left(-t + e^{1-t^2}\right) -\dfrac{1}{3}t^3 -\dfrac{1}{2}e^{1-t^2}+\dfrac{1}{2}e
&&\end{flalign}

단답형형

풀이

\begin{flalign} \sum_{n=1}^{\infty} \left( \left| a_n \right| + a_n \right) &=\sum_{n=1}^{\infty} 2a_{2n-1}\\
&=\dfrac{2a}{1-r^2}=\dfrac{40}{3} && \end{flalign}
\begin{flalign} \sum_{n=1}^{\infty} \left( \left| a_n \right| – a_n \right) &=\sum_{n=1}^{\infty} -2a_{2n}\\
&=\dfrac{-2a}{1-r^2}=\dfrac{20}{3} && \end{flalign}
$\dfrac{2a}{1-r^2}\times(-r)=\dfrac{20}{3}$, $\dfrac{40}{3}\times(-r)=\dfrac{20}{3}$

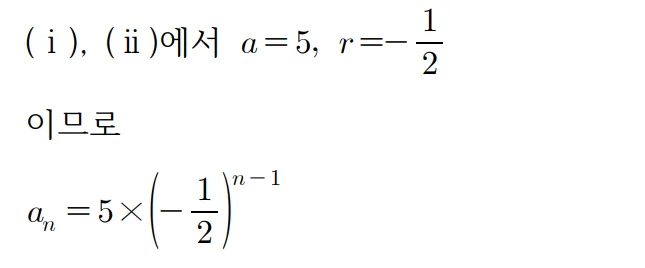
\begin{flalign} \lim_{n\to \infty}\sum_{k=1}^{2n} \left( (-1)^{\dfrac{k(k+1)}{2}}\times a_{m+k} \right) >\dfrac{1}{700}\\
& && \end{flalign}
\begin{flalign} & \lim_{n\to\infty} \left\{ 5 \times \left( -\dfrac{1}{2} \right)^{m-1} \times \sum_{k=1}^{2n} \left( (-1)^{\dfrac{k(k+1)}{2}} \times \left( -\dfrac{1}{2} \right)^k \right) \right\}\\
& \quad \quad >\dfrac{1}{700} && \end{flalign}
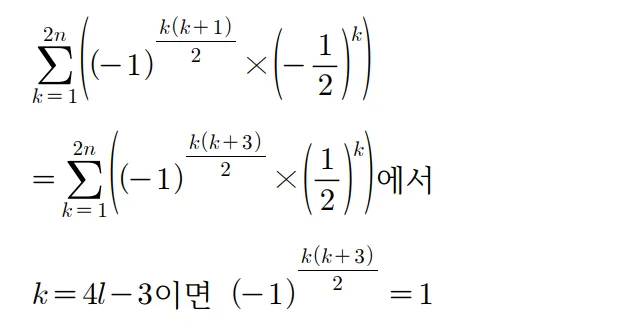


$n \to \infty$ 이면 $p \to \infty$이고 $2n=4p-2,\ 2n=4p$의 두 경우 모두 각 급수가 수렴하므로

정답 25

풀이





선택3. 기하
5지선다형

풀이


풀이


다른풀이


풀이



풀이



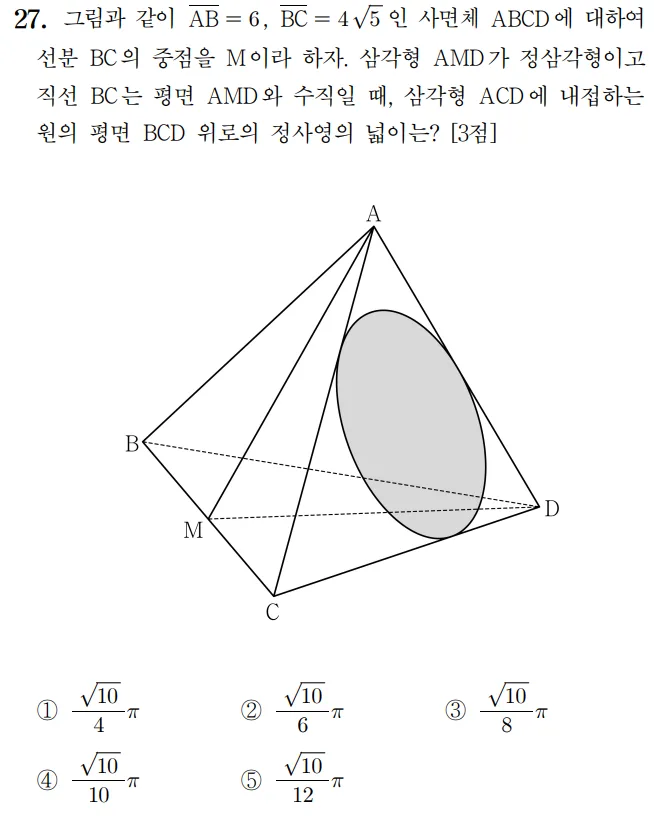
풀이




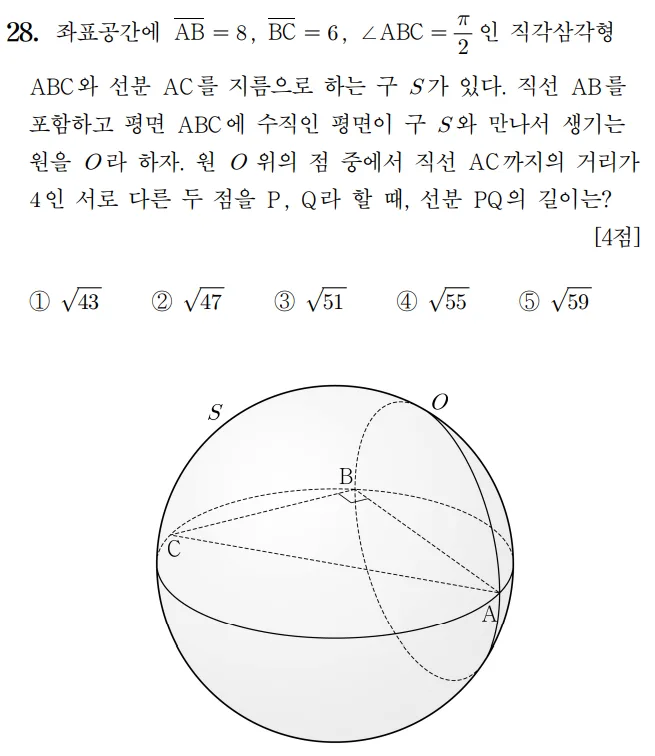
풀이
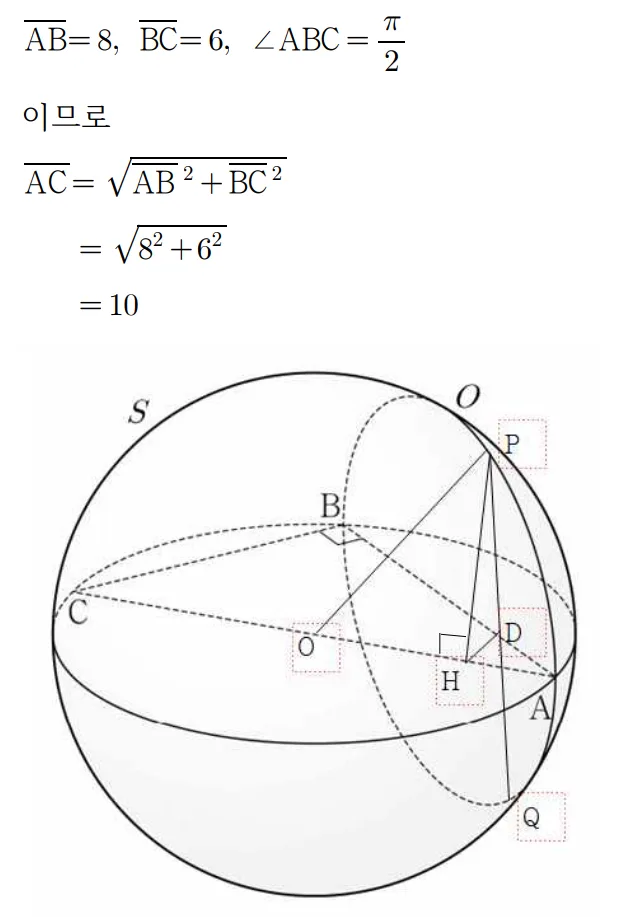



단답형

풀이

$\triangle{QF’F}$와 $\triangle{FF’P}$가 닮음 이므로

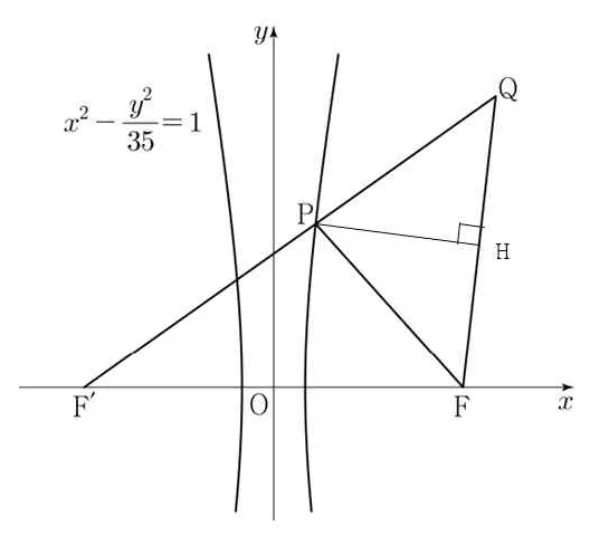


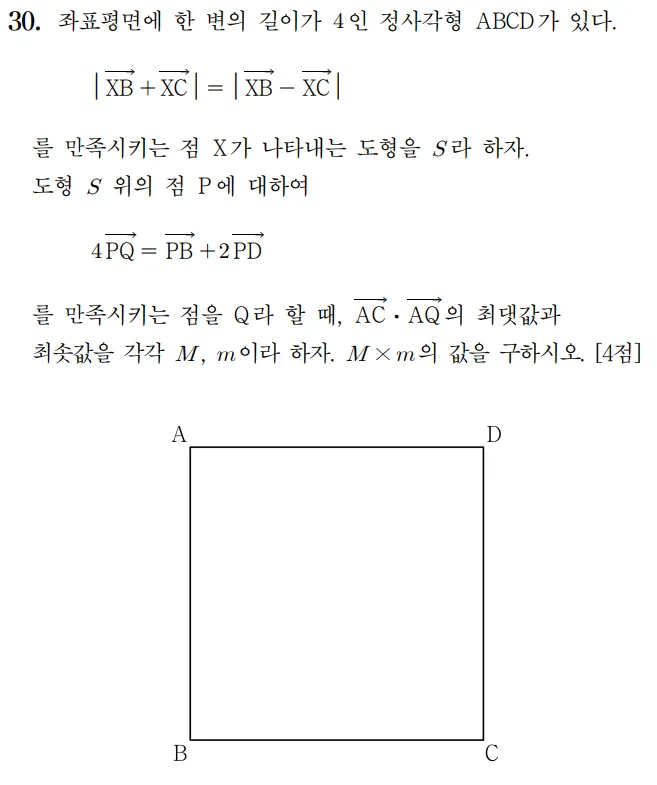
풀이



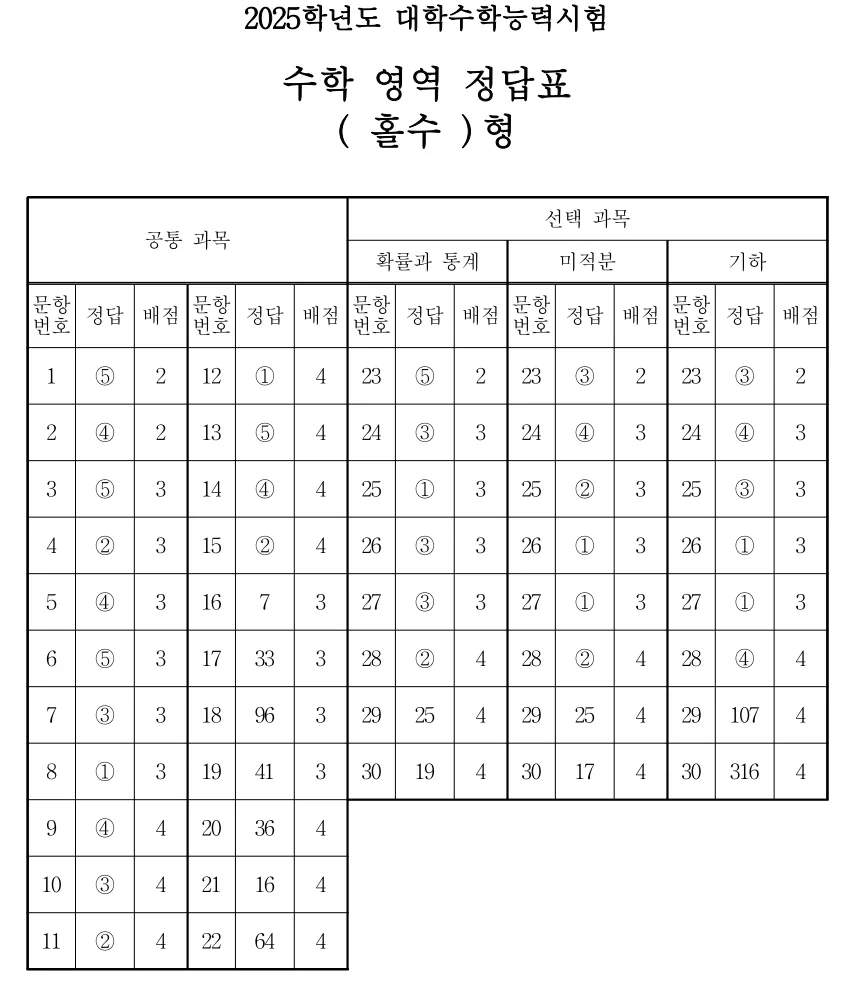
2025 수능 수학영역 정답표
연도별로 정리된 자료는 아래의 링크를 이용해 주세요.
