피타고라스 정리 증명 7가지 중학생 필수

피타고라스 정리를 단순히 $a^2+b^2=c^2$라는 공식 하나를 암기하는 수준에서 학습하면 안됩니다. 직각삼각형의 구조와 깊이 연결된 이 정리는, 도형의 넓이와 합동, 닮음, 대수적 전개 등 수학의 여러 갈래를 하나로 이어주는 관문 역할을 하기 때문입니다.

중학교 2학년 시기는 이제 막 직관적인 암기를 넘어 논리적인 이해를 쌓아가는 시기입니다. 피타고라스 정리를 다양한 방법으로 증명하는 과정은 단순히 한 가지 사실을 확인하는 데 그치지 않고, “왜 그런가?”라는 질문을 스스로 던지고 풀어나가는 수학적 사고력을 기르는 훈련이 됩니다.

이번 글에서는 피타고라스 정리의 의미, 직각삼각형의 조건, 피타고라스 수, 그리고 여러 가지 증명 방식에 대하여 정리해 보았습니다. 글을 끝까지 따라가다 보면 단순히 공식을 외우는 것이 아니라, 정리가 성립하는 원리와 수학적 연결고리를 이해하게 될 것이며, 이는 앞으로 도형 문제를 풀어가는 데 강력한 도구가 되어줄 것입니다.

피타고라스 정리

빗변의 길이가 $c$이고 나머지 두 변의 길이가 $a,\ b$인 직각삼각형에서 다음이 성립합니다.

$a^2 + b^2 = c^2$ (피타고라스 정리)

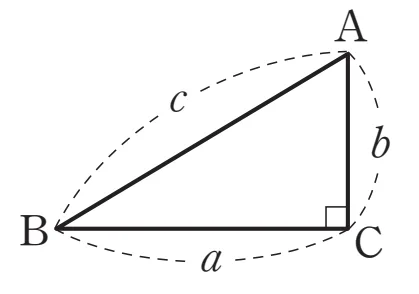
피타고라스 정리를 적용할 때 다음을 확인해야 합니다.

직각삼각형에서만 성립한다.
$c$: 빗변, 가장 긴 변, 직각의 대변이다.

재배열을 이용한 증명

재배열을 이용한 증명은 초등학교 수준에서 피타고라스 정리를 증명할 수 있는 방법으로 고대에서 구전으로 전승되는 방법과 바스카라 증명 (Bhaskara)이 알려져 있습니다.

고대 구전, 전승

중국, 인도, 그리스에서 고대(기원전 3세기 이전 추정)부터 구전으로 전해 내려온 증명이지만, 정확히 언제 처음 사용되었는지는 확실히 밝혀져 있지 않습니다. 유사한 기록은 기원전 3세기경 무렵의 중국 수학서인 주비산경에 비슷한 방법이 소개되어 있습니다.

빗변의 길이가 $c$ 이고 나머지 두 변의 길이가 $a,\ b$인 합동인 직각삼각형 네 개를 한 변의 길이가 $a+b$인 정사각형에 다음과 같이 채워 넣을 수 있습니다. (출처: 위키백과)

합동인 직각삼각형 4개를 한 변이 $a+b$인 정사각형의 꼭짓점에 배열하고 $\bbox[#fcd2f8]{\text{남은 영역}}$은 다음과 같이 계산할 수 있습니다.
- $\bbox[#fcd2f8]{c^2}$
합동인 직각삼각형 4개를 두 개씩 모아 직사각형을 만들고 한 변이 $a+b$인 정사각형에 배열하고 $\bbox[#e2f0d9]{\text{남은 영역}}$은 다음과 같이 계산할 수 있습니다.
- $\bbox[#e2f0d9]{a^2+b^2}$

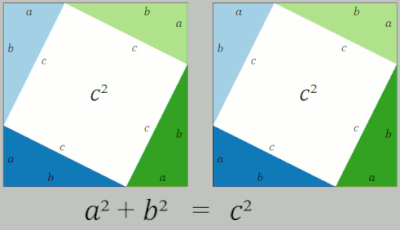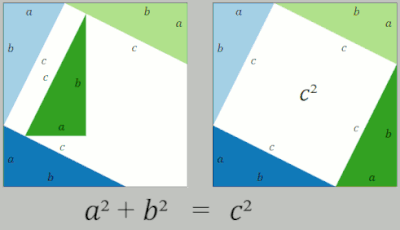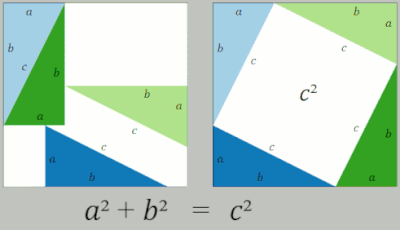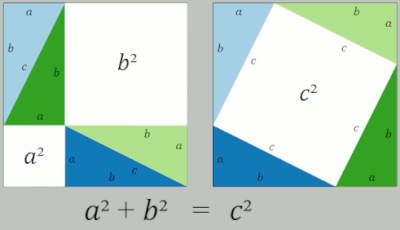
위의 결과를 정리하면 다음과 같이 피타고라스 정리가 성립함을 알 수 있습니다.

(전체 정사각형 넓이) $-$ (직각삼각형 넓이 합)
- $\bbox[#e2f0d9]{a^2+b^2}=\bbox[#fcd2f8]{c^2}$

바스카라 증명 Bhaskara

7세기 인도 수학자 바스카라(Bhaskara)는 “Behold!”(보라!)라는 간단한 말과 그림만으로 피타고라스 정리를 도형을 재배열하여, 피타고라스 정리를 직관적으로 증명했습니다. 바스카라의 증명은 다음과 같습니다.

빗변의 길이가 $c$ 이고 나머지 두 변의 길이가 $a,\ b$인 합동인 직각삼각형 네 개를 한 변의 길이가 $c$인 정사각형에 아래와 같이 채워 넣고, 남은 정사각형을 재배열하면 큰 정사각형의 넓이를 두 정사각형 넓이의 합으로 나타낼 수 있습니다.

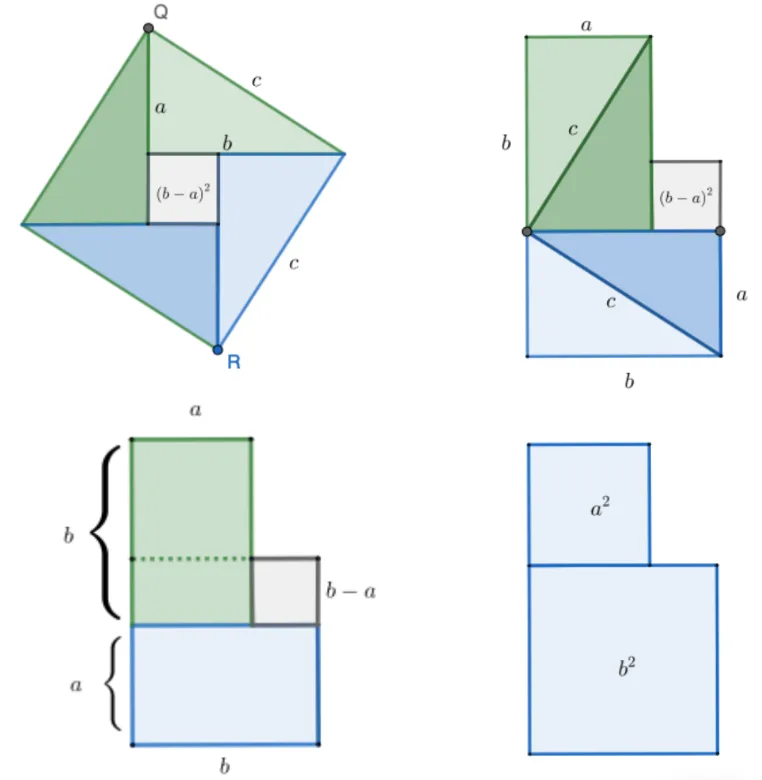
처음 주어진 큰 정사각형의 넓이와 마지막 두 정사각형 넓이의 합이 같으므로 다음이 성립함을 알 수 있습니다.

$a^2+b^2=c^2$

출처: https://scholarworks.boisestate.edu/

합동을 이용한 증명

합동을 이용한 피타고라스 증명은 기원전 3세기경 유클리드 원론에 실려 있는 방법으로, 이를 이해하려면 삼각형의 합동과 평행선 사이의 도형의 넓이에 대한 학습이 선행되어야 합니다. 따라서 피타고라스 정리를 중학교 2학년 수준에서 다룰 때 사용하는 증명입니다.

삼각형의 합동을 이용해 피타고라스 정리를 증명하는 유클리드 방법은 다음과 같습니다.

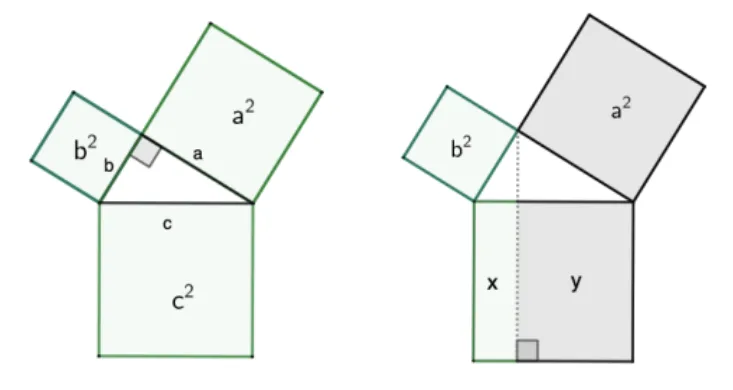
빗변의 길이가 $c$ 이고 나머지 두 변의 길이가 $a,\ b$인 직각삼각형의 세 변을 한 변으로 하는 정삼각형을 그리고 다음과 같은 사실을 증명하면 피타고라스 정리가 성립함을 증명할 수 있습니다.

$a^2=y,\ b^2=x$

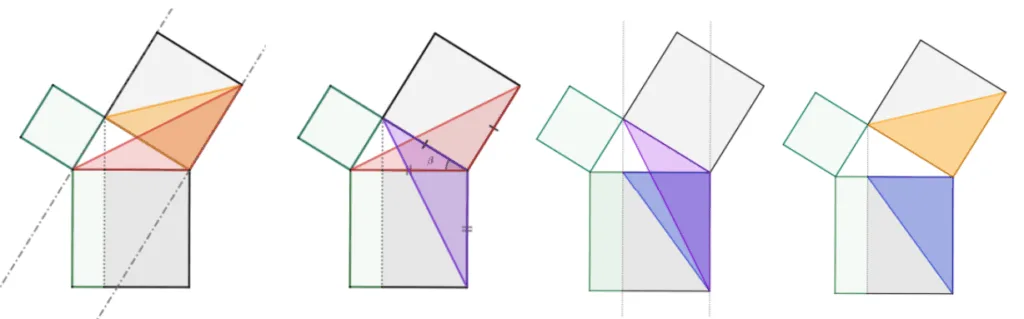
위의 그림을 통해 다음과 같은 사실을 알 수 있습니다.

$\bbox[#f7d19f]{\triangle}=\bbox[#f7d5d4]{\triangle}$ (평행선)
$\bbox[#f7d5d4]{\triangle}\equiv \bbox[#e2cdfb]{\triangle}$ (SAS합동)
- 끼인각: $\beta+90^\circ$
$\bbox[#e2cdfb]{\triangle} = \bbox[#a2ace0]{\triangle}$ (평행선)

결과적으로 $\bbox[#f7d19f]{\triangle}=\bbox[#a2ace0]{\triangle}$이고 따라서 $a^2=y$임을 알 수 있습니다. 비슷한 방법으로 $b^2=x$도 성립하고 따라서 다음이 성립합니다.

$a^2+b^2=c^2$

출처: https://scholarworks.boisestate.edu/

닮음을 이용한 증명

존 윌리스(John Wallis)는 직각삼각형에서 빗변에 내린 수선으로 인해 생긴 두 작은 삼각형이 원래의 큰 삼각형과 닮음이라는 점을 이용하여 피타고라스 정리를 증명했습니다. 이 증명은 중학교 2학년 닮음을 학습한 후 도입할 수 있는 증명입니다.

$\angle{C} = 90°$인 직각삼각형 $\triangle{ABC}$의 점 $C$에서 $\overline{AB}$에 내린 수선의 발을 $D$에 대하여 다음이 성립합니다.

$\triangle{ABC} \sim \triangle{CBD}$ (AA 닮음)

$\angle{B}$: 공통
$\angle{ACB} = \angle{CDB} = 90°$

$c:a = a:\overline{DB}$ 이고 $a^2 = c \times \overline{DB} \cdots ㄱ$

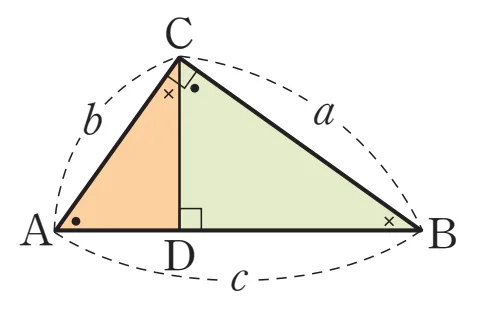
$\triangle{ABC} \sim \triangle{ACD}$ (AA 닮음)이므로 같은 방법으로
$c:b = b:\overline{AD}$이고 $b^2 = c \times \overline{AD} \cdots ㄴ$

ㄱ, ㄴ식을 변변 더하여 정리하면 다음과 같습니다.
\begin{flalign} a^2 + b^2 &= c \times \overline{DB} + c \times \overline{AD} \\
&= c \times (\bbox[#dcff8d]{\overline{DB} + \overline{AD}})\\
&= c \times \bbox[#dcff8d]{c}= c^2&&\end{flalign}

결과적으로 피타고라스 정리 $a^2+b^2=c^2$가 성립함을 알 수 있습니다.

곱셈공식을 이용한 증명

중학교 3학년 곱셈공식을 배우면 문자가 포함된 다항식을 거듭제곱할 수 있습니다. 이를 이용하면 재배열을 이용한 증명을 수식으로 변형하여 피타고라스 정리가 성립함을 대수적(문자를 이용한 식)으로 보일 수 있습니다. 이는 중학교 3학년에서 피타고라스 정리를 도입할 때 사용되었던 방법으로 현행 교육과정에서는 곱셈공식의 응용으로 다루어지고 있습니다.

대수적 증명1

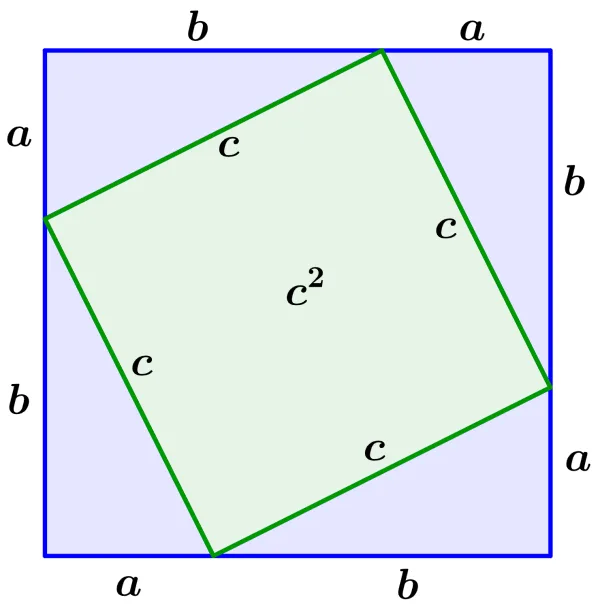
빗변의 길이가 $c$ 이고 나머지 두 변의 길이가 $a,\ b$인 합동인 직각삼각형 네 개를 한 변이 $a+b$인 정사각형에 아래와 같이 채워 넣을 때, 다음 사각형의 넓이는 다음과 같이 두 가지로 나타낼 수 있습니다.

$(a+b)^2=a^2+2ab+b^2$
$4\times\bbox[#e6e6fe]{\dfrac{1}{2}ab}+\bbox[#e8f4e8]{c^2}=\bbox[#e6e6fe]{2ab}+\bbox[#e8f4e8]{c^2}$

따라서 $a^2+b^2=c^2$이 성립합니다.

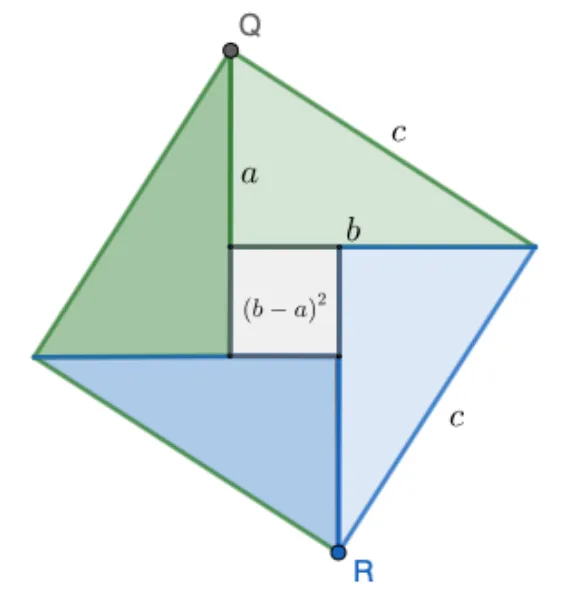
대수적 증명2 Bhaskara

빗변의 길이가 $c$ 이고 나머지 두 변의 길이가 $a,\ b$인 합동인 직각삼각형 네 개를 한 변의 길이가 $c$인 정사각형에 아래와 같이 채워 넣으면 큰 정사각형 넓이$c^2$은 다음과 같습니다.

\begin{flalign}4\times&\bbox[#a2c5a3]{\dfrac{1}{2}ab}+(b-a)^2\\
&=\bbox[#a2c5a3]{2ab}+a^2+b^2-2ab\\
&=a^2+b^2&&\end{flalign}

대수적 증명3 가필드 증명

직각삼각형 $\triangle{ABC}$와 합동인 직각삼각형 $\triangle{CDE}$를 이용해 만든 사다리꼴 $\square{ABDE}$의 넓이는 다음과 같이 두 가지 방법으로 구할 수 있습니다.

$\triangle{ABC}+\triangle{CDE}+\triangle{ACE}$
$=2\times \dfrac{ab}{2}+\dfrac{1}{2}c^2\cdots ㄱ$
$\square{ABDE}=\dfrac{1}{2}\times(a+b)\times(a+b)$
$=\dfrac{1}{2}\times\{a^2+b^2+2ab\}\cdots ㄴ$

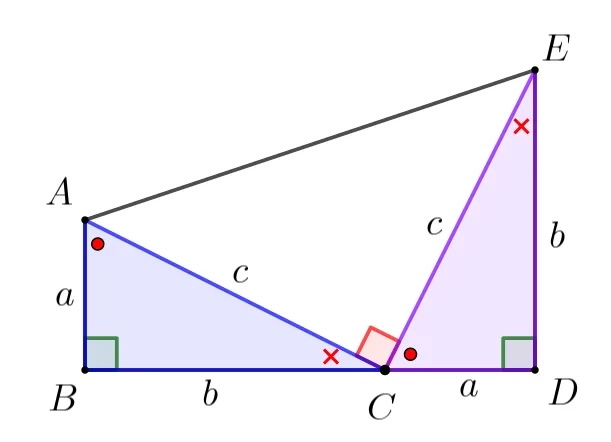
$ㄱ,\ ㄴ$의 결과를 종합하면 $a^2+b^2=c^2$이 성립함을 알 수 있습니다.

직각삼각형의 성질과 조건

피타고라스 정리가 성립하는 것은 직각삼각형의 성질임을 알 수 있습니다. 이제 피타고라스 정리를 만족하는 삼각형은 직각 삼각형이 되는지 확인해 봐야 합니다.

직각삼각형 $\xrightarrow[]{\bigcirc}$ 피타고라스 정리
피타고라스 정리 $\xrightarrow[]{?}$ 직각삼각형

세 변의 길이가 $a,\ b,\ c$인 삼각형이 $a^2+b^2=c^2$을 만족하면 직각삼각형이다

두 변의 길이가 $a,\ b$이고 끼인각이 직각인 삼각형을 작도하면 다음이 성립합니다. (빗변의 길이는 모르는 상태)

직각삼각형: 피타고라스 정리 적용
$a^2+b^2={\color{red}\square}^2$
조건에서, ${\color{red}\square}^2=c^2$이고 ${\color{red}\square}=c$

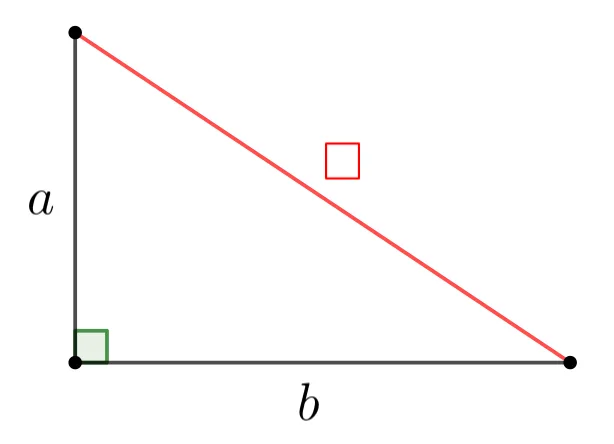
세 변의 길이가 $a,\ b,\ c$인 삼각형(SSS합동)은 유일하기이기 때문에 피타고라스 정리를 만족하는 삼각형은 직각삼각형이 됩니다.

피타고라스 수

피타고라스 수: 피타고라스 정리 $a^2 + b^2 = c^2$ 을 만족시키는 세 자연수 $a,\ b,\ c$
예: (3, 4, 5), (5, 12, 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 12, 15)

대부분 중학교 피타고라스 문제는 자연수로 떨어지는 값을 선호하기 때문에 다음 수의 조합을 암기하는 것이 큰 도움이 됩니다.

[이미지 출처: 개념원리]

목차