평행선 사이의 삼각형의 넓이는 중학교 수학에서 반드시 짚고 넘어가야 할 핵심 개념입니다. 왜 같은 넓이가 되는지를 이해하면 문제 해결력이 크게 높아집니다.
이번 글에서는 평행선과 삼각형, 사다리꼴, 평행사변형의 넓이 관계를 차례대로 정리하고, 증명 아이디어까지 함께 담았습니다. 끝까지 읽으시면 개념이 훨씬 잘 정리될 것입니다.
평행선과 삼각형의 넓이
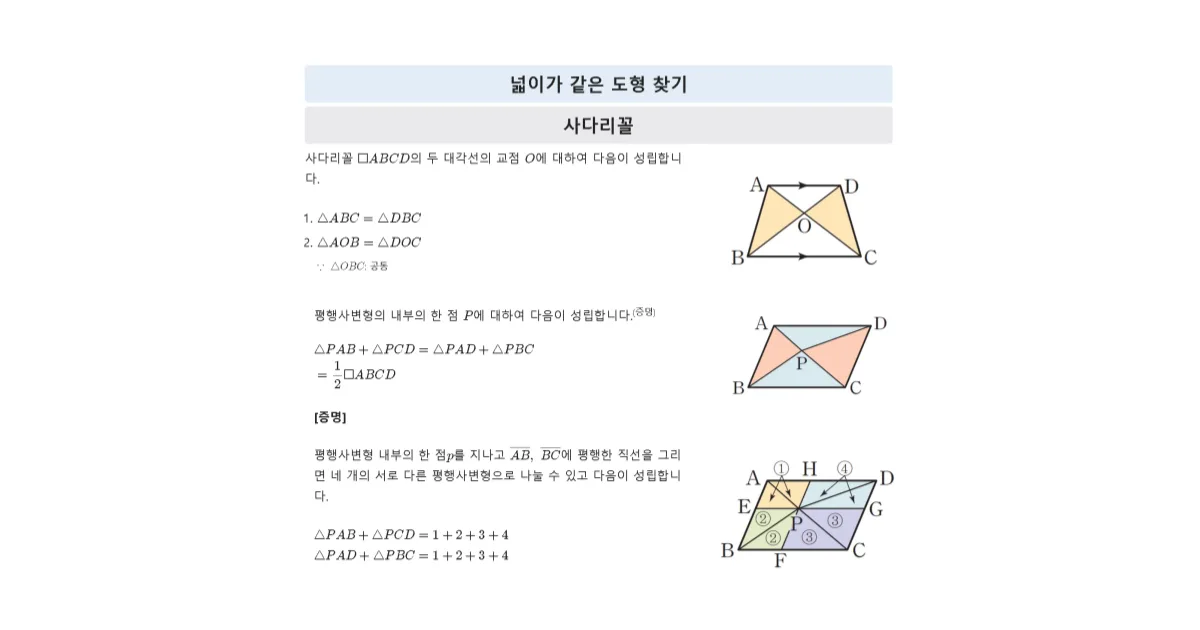
두 직선 $l,\ m$이 평행하고 두 직선사이의 거리가 $h$일 때, 밑변이 공통으로 하는 두 삼각형에 대하여 다음이 성립합니다.
- $\triangle{ABC}=\triangle{DBC}=\dfrac{1}{2}ah$
- $\bbox[#d8eaee]{\triangle}=\bbox[#fad5e5]{\triangle}$ ($\because \ \bbox[#d0d0e8]{\triangle}$ 공통)
높이가 같은 삼각형의 넓이
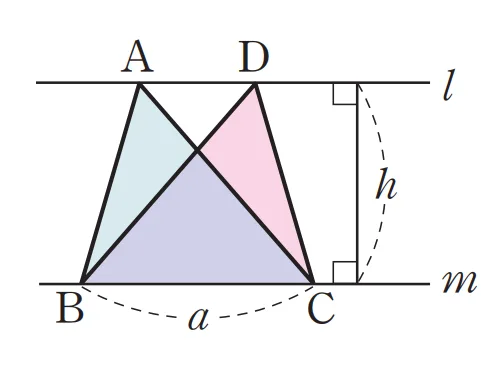
높이가 같은 삼각형 $\triangle{ABC},\ \triangle{ACD}$의 넓이 비는 밑변의 길이 비와 같습니다.
$\triangle{ABC} : \triangle{ACD}=\overline{BC}:\overline{CD}$
넓이가 같은 도형 찾기
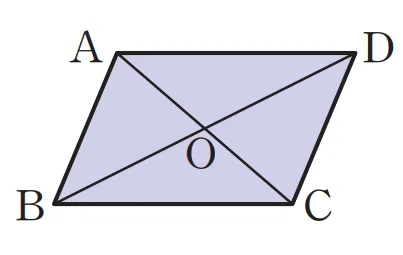
사다리꼴
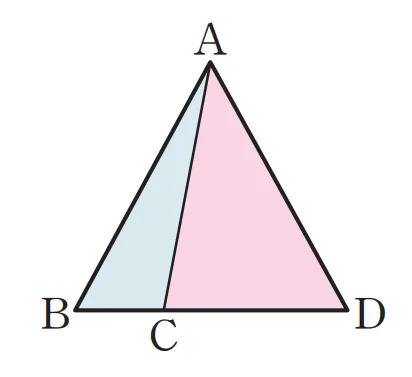
사다리꼴 $\square{ABCD}$의 두 대각선의 교점 $O$에 대하여 다음이 성립합니다.
- $\triangle{ABC}=\triangle{DBC}$
- $\triangle{AOB}=\triangle{DOC}$
$\because \ \triangle{OBC}$: 공통
평행사변형
평행사변형의 넓이는 한 대각선에 의해 이등분됩니다.
(한 대각선에 의해 합동인 삼각형이 두 개 만들어지기 때문)
\begin{flalign}&\triangle{ABC}=\triangle{ACD}=\triangle{ABD}=\triangle{BCD}\\
&=\dfrac{1}{2}\square{ABCD}&&\end{flalign}
평행사변형의 넓이는 두 대각선에 의해 사등분됩니다.
(대각선이 서로 다른것을 이등분 하기 때문)
\begin{flalign}&\triangle{ABO}=\triangle{BCO}=\triangle{CDO}=\triangle{DAO}\\
&=\dfrac{1}{4}\square{ABCD}&&\end{flalign}
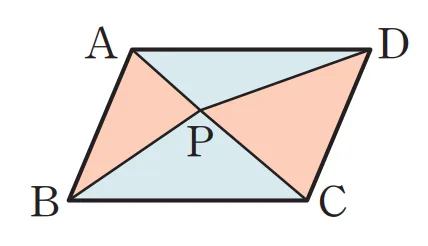
평행사변형의 내부의 한 점 $P$에 대하여 다음이 성립합니다.(증명)
\begin{flalign}&\triangle{PAB}+\triangle{PCD}=\triangle{PAD}+\triangle{PBC}\\
&=\dfrac{1}{2}\square{ABCD}&&\end{flalign}
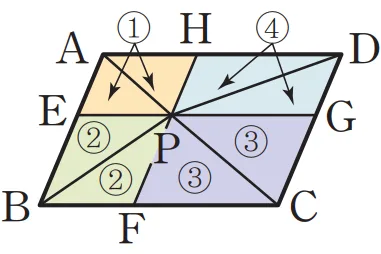
[증명]
평행사변형 내부의 한 점$p$를 지나고 $\overline{AB},\ \overline{BC}$에 평행한 직선을 그리면 네 개의 서로 다른 평행사변형으로 나눌 수 있고 다음이 성립합니다.
$\triangle{PAB}+\triangle{PCD}=1+2+3+4$
$\triangle{PAD}+\triangle{PBC}=1+2+3+4$
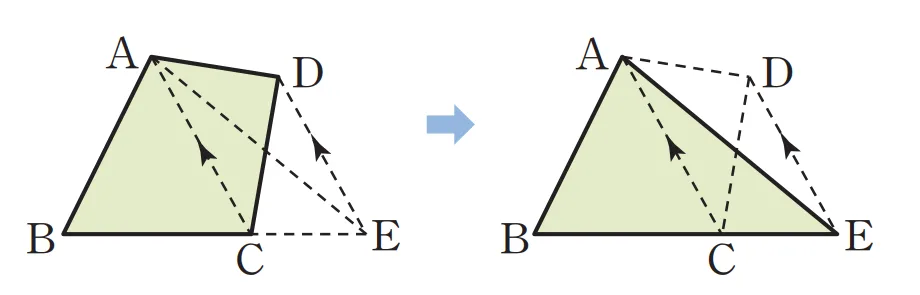
평행선 이용
사각형 $\square{ABCD}$에서 꼭짓점 $D$를 지나고 대각선 $\overline{AC}$와 평행한 직선이 변BC의 연장선과 만나는 점$D$에 대하여
- $\triangle{ACD}=\triangle{ACE}$
평행선 사이의 삼각형의 넓이 - $\square{ABCD}=\triangle{ABE}$
[이미지 출처: 개념원리]