“평행사변형의 성질, 그냥 외우기만 하셨나요?”
도형을 진짜 이해하려면 단순한 암기에서 벗어나 왜 그런 성질이 성립하는지를 파악하는 것이 중요합니다. 이 글에서는 평행사변형의 정의부터 시작해, 4가지 필수 성질을 도형과 삼각형 합동 원리를 통해 직접 증명하는 과정을 다루고 있습니다.
중학교 수학에서 반드시 알아야 할 내용을 쉽고 논리적으로 풀어낸 설명과 함께 확인해보세요. 끝까지 읽고 나면, 어떤 도형 문제도 논리적으로 접근할 수 있는 확신이 생길 것입니다.
평행사변형
사각형 $ABCD$에 대하여 평행사변형은 다음과 같이 정의 합니다.
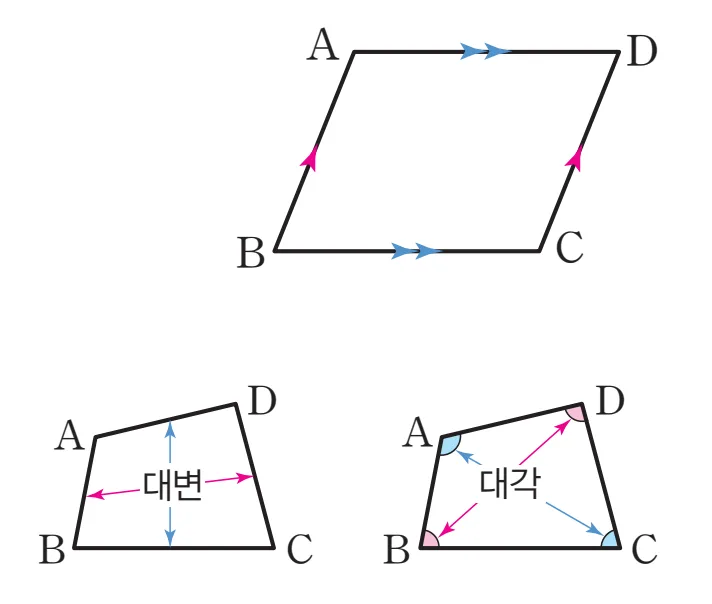
평행사변형: 두 쌍의 대변이 각각 평행한 사각형
그림에서 $\overline{AB} \pa \overline{CD}$, $\overline{AD} \pa \overline{BC}$
- 대변: 서로 마주보는 변
$\overline{AB}$ 와 $\overline{CD}$, $\overline{AD}$ 와 $\overline{BC}$ - 대각: 서로 마주보는 각
$\angle A$ 와 $\angle C$, $\angle B$ 와 $\angle D$
평행사변형의 성질

평행사변형 $\square{ABCD}$에 대하여 다음의 성질이 성립합니다.
- 성질1. 두 쌍의 대변의 길이가 각각 같다.
- 성질2. 두 쌍의 대각의 크기가 각각 같다.
- 성질3. 이웃하는 두 내각의 크기의 합이 모두 180도이다.
- 성질4. 두 대각선은 서로 다른것을 이등분한다.
평행사변형의 성질 증명
성질 1,2,3 증명
평행사변형 $\square{ABCD}$에서 대각선 $\overline{AC}$를 그으면 두 삼각형으로 나누어 지고, $\overline{AC}$가 공통, 양 끝각이 엇각으로 같아 $\triangle{ABC} \equiv \triangle{CDA}$(ASA)입니다.
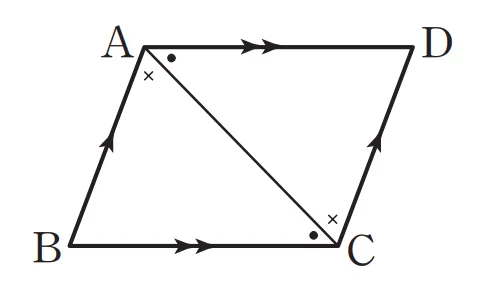
따라서 다음이 성립합니다.
- 성질1. $\overline{AB} = \overline{CD}$, $\overline{AD} = \overline{BC}$
- 성질2. $\angle{A}=\angle{C}$, $\angle{B}=\angle{D}$
- 성질3. $\angle{A}+\angle{B}=180^\circ$, $\angle{B}+\angle{C}=180^\circ\cdots$
성질4 증명
평행사변형 $\square{ABCD}$에서 두 대각선 $\overline{AC}$와 $\overline{BD}$의 교점을 $O$라 할 때, 서로 마주보는 삼각형 $\triangle{ABO}$, $\triangle{CDO}$에 대하여 $\overline{AB} = \overline{CD}$(성질1)이고 양 끝각이 엇각으로 같습니다. 따라서 다음이 성립합니다.
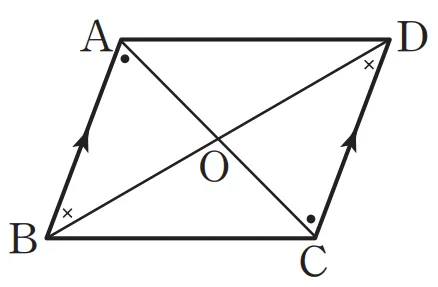
$\triangle{ABO} \equiv \triangle{CDO}$ ASA합동이고, $\overline{AO} = \overline{CO}$, $\overline{BO} = \overline{DO}$ (두 대각선이 서로 다른 것을 이등분)
이번시간에는 평행사변형의 성질에 대해 학습하였습니다. 그렇다면, 어떤 사각형이 평행사변형이 되는지는 어떻게 판단할 수 있을까요? 다음 글에서는 평행사변형의 조건에 대한 내용을 정리해 보도록 하겠습니다.
- $\square{ABCD}$가 평행사변형 $\Rightarrow$ 성질
- 조건 $\Rightarrow$ $\square{ABCD}$가 평행사변형
[이미지 출처: 개념원리]
