평면과 직선의 위치관계 추론 문제

이번 시간에는 세 평면과 직선의 위치관계를 추론하는 문제를 풀어보도록 하겠습니다. 주어진 조건에서 평면과 직선이 공간에서 어떻게 위치할 수 있는지 판단하는 방법을 익혀 보도록 합시다.

평면에서 세 직선의 위치관계

한 평면위의 서로 다른 세 직선 $l,\;m,\;n$ 에 대하여 잘못된 것을 바르게 고쳐라.

1. $l⫽m$이고 $m⫽n$이면 $l⫽n$이다.
2. $l⫽m$이고 $m\perp n$이면 $l⫽n$이다.
3. $l\perp m$이고 $m\perp n$이면 $l⫽n$이다.

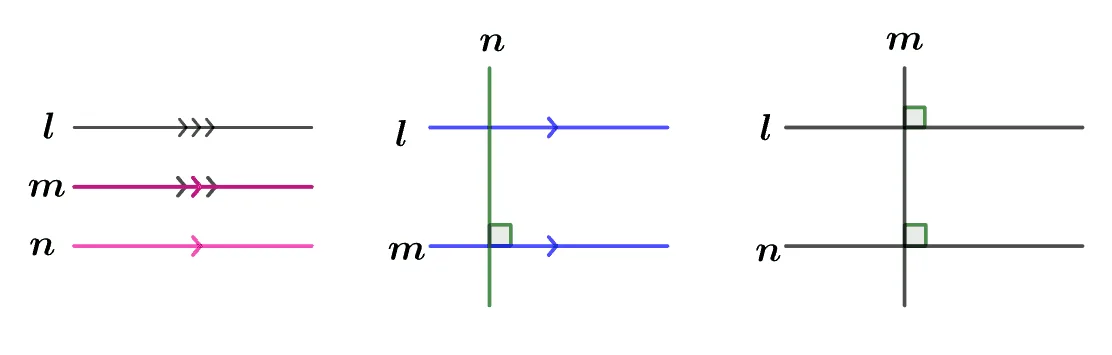
1. T
2. F $l⫽n \rightarrow l\perp n$
3. T

공간에서 위치관계

공간에서 두 직선, 직선과 평면, 두 평면의 위치관계를 고려할 때 입체도형을 이용하면 편리하다. 여기서는 직육면체를 이용하여 다음과 같은 과정으로 추론해 보자.

[공간에서 위치관계 확인 요령]

1. $\bbox[#ffff00]{\text{직육면체}}$이용 $\rightarrow$ 대략적으로 파악
2. 사고 확장 $\rightarrow$ 공간에서 가능한 위치관계 고려

세 직선의 위치관계 추론

공간에서 서로 다른 세 직선 $l,\;m,\;n$ 에 대하여 잘못된 것을 바르게 고쳐라.

1. $l⫽m$이고 $m⫽n$이면 $l⫽n$이다.
2. $l⫽m$이고 $m\perp n$이면 $l\perp n$이다.
3. $l\perp m$이고 $m\perp n$이면 $l⫽n$이다.

참고로 위의 사실은 평면에서는 모두 참(True)이다.

위와 같은 경우 두 조건에서 중복되는 $m$을 고정하고 나머지 조건을 만족하는 모든 경우를 고려하는 것이 좋다.

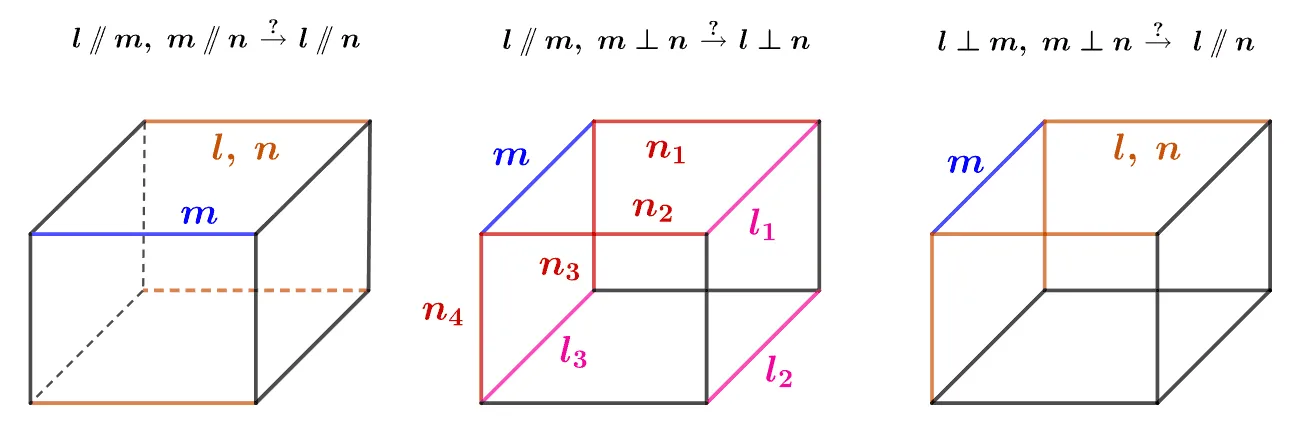
1. T
2. F $l,\;n$ 수직 또는 꼬인위치
3. F $l,\;n$ 만나거나, 평행하거나, 꼬인위치에 있을 수 있다.

직육면체에서 모든 위치관계가 드러나는 것은 아니다. 따라서 직육면체는 위치관계를 빠짐없이 고려할 수 있도록 하는 보조 역할임을 기억하자.

평면과 직선의 위치관계 추론

공간에서 서로 다른 두 직선 $l,\;m$과 $P, Q$에 대하여 잘못된 것을 바르게 고쳐라.

1. $l ⫽P$이고 $m ⫽P$이면 $ l⫽m$이다.
2. $l ⫽m$이고 $l\perp P$이면 $m\perp P$이다.
3. $l ⫽P$이고 $l ⫽Q$이면 $P ⫽Q$이다.
4. $l\perp P$이고 $m\perp P$이면 $l ⫽m$이다.

직육면체로 대략적인 위치관계를 파악하고, 사고를 확장하여 공간에서 가능한 위치관계를 빠짐없이 고려해 보는 연습을 해보자.

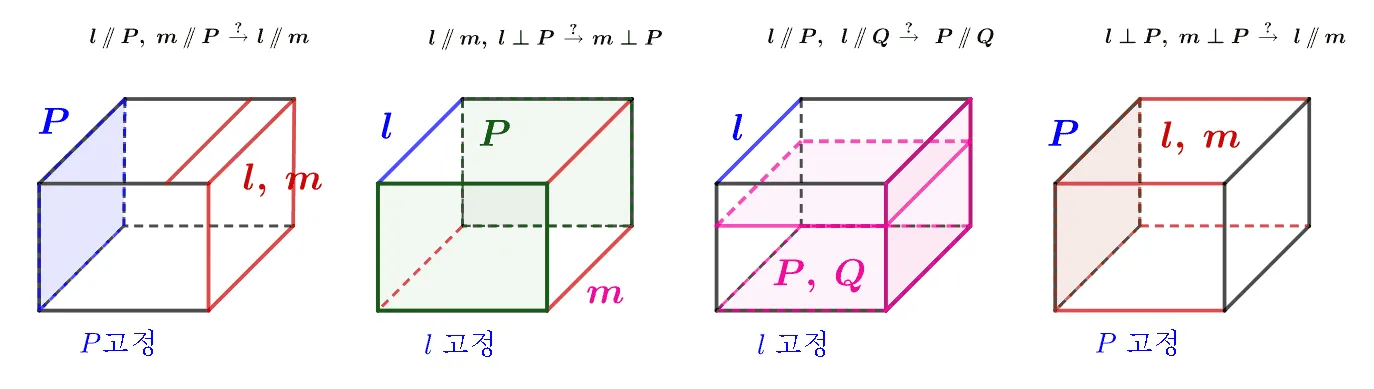
1. F $l,\;m$은 만나거나 평행하거나 꼬인위치에 있을 수 있다.
2. T
3. F $P, Q$는 만나거나 평행할 수 있다.
4. T

세 평면의 위치관계 추론

공간에서 서로 다른 세 평면 $P,\;Q,\;R$에 대하여 잘못된 것을 바르게 고쳐라.

1. $P⫽Q$이고 $Q⫽R$이면 $P⫽R$이다.
2. $P⫽Q$이고 $P\perp R$이면 $Q⫽R$이다.
3. $P\perp Q$이고 $P\perp R$이면 $Q\perp R$이다.

마찬 가지로 직육면체로 대략적으로 파악하고, 공간으로 사고를 확장하여 모든 가능한 위치관계를 정리해 보기로 하자.

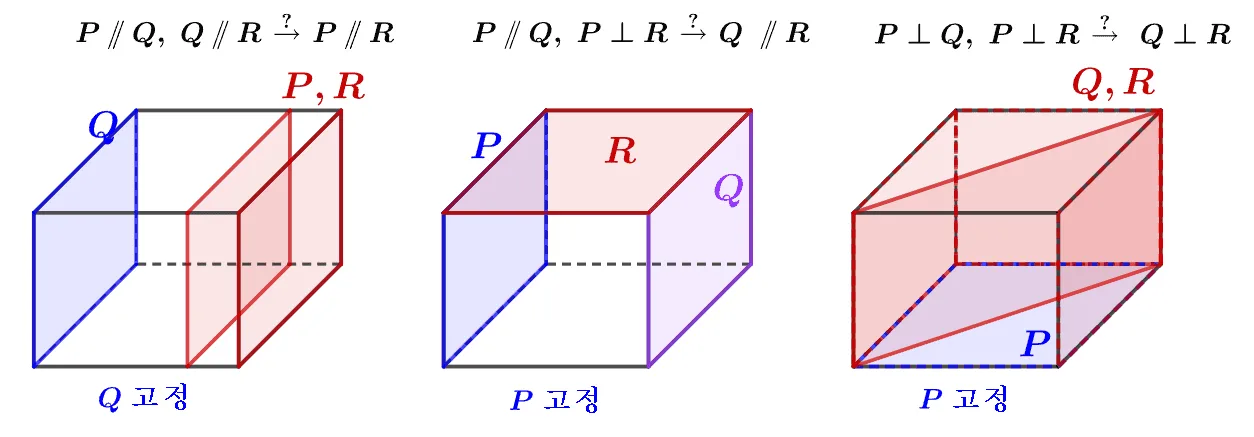
1. T
2. F $Q,\;R$ 은 수직이다.
3. F $Q\; R$ 은 만나거나 평행할 수 있다.

맺음말

입체도형을 다룰 때 위치관계를 확실히 이해하는 것은 매우 중요합니다. 이번 글을 통해 평면과 직선의 위치관계에 대한 이해가 깊어졌기를 바랍니다.