직선의 방정식과 일차함수의 관계

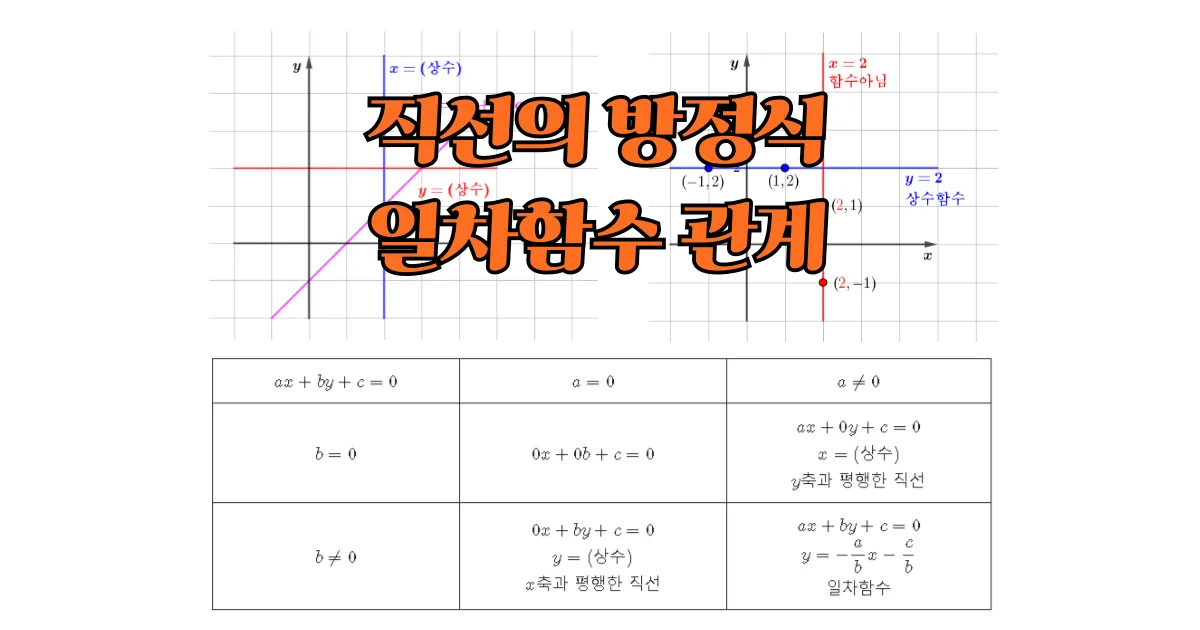
좌표평면 위의 직선은 모두 일차함수로 표현될까요? 단순히 직선이라면 ‘기울기와 절편’만 알면 충분할 것 같지만, 사실 모든 직선이 일차함수는 아닙니다. 특히 $x$축이나 $y$축과 평행한 직선은 일차함수의 범주를 벗어나기 때문에, 이를 수학적으로 다루기 위해 보다 일반화된 표현, 즉 직선의 방정식이 필요합니다.

이 글에서는 일차함수와 직선의 차이를 직관적으로 이해할 수 있도록 그래프와 표를 활용해 설명하고, 왜 $ax + by + c = 0$이라는 식이 모든 직선을 아우르는 중요한 식인지 알아봅니다. 마지막까지 읽으면 ‘직선의 함수라고 하지 않는지?’에 대한 궁금증까지 말끔히 해결될 것 입니다.

일차함수와 직선

좌표평면에서 $y=ax+b,\;(a\neq 0)$꼴의 일차함수는 직선으로 나타낼 수 있습니다. 하지만 $x$축과 평행인 직선, $y$축에 평행인 직선은 일차함수로 표현할 수 없습니다.

• 일차함수 $y=ax+b,\;(a\neq 0)$로 표현할 수 없는 직선
  1. $x$축과 평행한 직선: $y=(\text{상수})$꼴
     • 기울기가 $0$인 직선
     • $a=0$일 때 $y=0\times x+b$, 따라서 $y=(\text{상수})$
  2. $y$축과 평행한 직선: $x=(\text{상수})$꼴
     • 기울기가 무한대 인 직선 ($a=\infty$)
     • $x$축과 평행한 직선의 표현: $x=(\text{상수})$

직선의 방정식

일차함수로는 $x=\text{(상수)}$, $y=\text{(상수)}$와 같은 직선을 나타낼 수 없고, 따라서 좌표평면상의 직선을 모두 표현할 수 없습니다. 좌표평면의 직선을 일반화된 식으로 나타내기 위해서 일차함수와 비슷한 구조인 $ax+by+c=0$꼴의 일차방정식을 이용하는 것을 고려해 볼 수 있습니다.

$ax+by+c=0$꼴의 방정식을 $a=0,\;a\neq0$, $b=0,\;b\neq0$인 경우로 나누어 표로 정리하면 다음과 같습니다.

$ax+by+c=0$	$a=0$	$a\neq0$
$b=0$	$0x+0y+c=0$ 일차방정식아님 ($\bbox[#ffc5fd]{\text{제외}}$)	$ax+0y+c=0$ $x=-\dfrac{c}{a}(\text{상수})$ $y$축과 평행한 직선
$b\neq0$	$0x+by+c=0$ $y=-\dfrac{c}{b}(\text{상수})$ $x$축과 평행한 직선	$ax+by+c=0$ $y=-\dfrac{a}{b}x-\dfrac{c}{b}$ 일차함수

위의 결과를 통해 일차방정식 $ax+by+c=0$은 좌표평면의 직선을 모두 표현할 수 있음을 알 수 있습니다. 따라서 이를 직선의방정식이라고 합니다.

1. 직선의 방정식 정의: 일차방정식 $ax+by+c=0$
2. 관계식 표현: $ax+by+c=0$ ($a\neq0 \; \bbox[#ffff00]{\text{또는}} \; b\neq0$)

위의 사실로 부터 직선의 방정식은 일차함수 뿐 아니라 좌표축에 평행한 직선 까지 포함하는 수학적 개념임을 알 수 있습니다.

직선의 함수가 아닌 이유

관계식을 통해 확인

$ax+by+c=0$ ($a\neq0 \; \bbox[#ffff00]{\text{또는}} \; b\neq0$)이 직선의 함수가 될 수 없는 이유는 다음과 같습니다.

1. $a\neq0,\;b\neq0$인 경우 $ax+by+c=0$은 일차 함수이다.
2. $a=0,\;b\neq0$인 경우 $0x+by+c=0$이고
   • 모든 $x$값에 대해 $y=-\dfrac{c}{b}$로 하나로 결정되고 따라서 함수이다.
   • 이렇게 $y=(\text{일정 상수})$인 함수를 상수함수라 합니다.
3. $a\neq0,\;b=0$인 경우 $ax+0y+c=0$이고
   • $y$의 계수가 $0$이므로 $y$의 값에 상관 없이 $x=-\dfrac{c}{a}=(\text{상수})$
   • $x(\text{상수})\rightarrow y(\text{모든수})$: 함수가 아니다.

$ax+0y+c=0,\;(a\neq0)$는 함수가 아니므로 직선의 함수라고 하지 않고, 직선의방정식이라고 합니다.

그래프를 이용한 확인

좌표축에 평행한 직선의방정식은 다음과 같이 표현할 수 있고 그래프 위의 점을 통해 함수가 되는지 확인 할 수 있습니다.

1. $y=2$위의 점: $\cdots(-1,2),\;(1,2)\cdots$
   • $x$ 값에 따라 $y$값이 하나로 결정
   • $-1\rightarrow2,\;0\rightarrow2,\;1\rightarrow2$
   • $y=2$는 상수함수이다.
2. $x=2$위의 점: $\cdots(2,-1),\;(2,1)\cdots$
   • $x=2$ 일 때 여러 $y$값을 갖음.
   • $2\rightarrow \cdots -1,\;0,\;1\cdots$
   • $x=2$는 함수가 아니다.