이번 시간에는 이전 시간에 배운 평행선과 선분의 길이의 비를 응용해 삼각형, 사각형, 사다리꼴의 중점을 연결하면 일정한 평행 관계와 길이 비가 성립는 중점연결정리에 대해 정리해 보도록 합시다. 예를 들어, 삼각형에서는 두 변의 중점을 잇는 선분이 나머지 한 변과 평행하고 그 길이는 절반이 됩니다. 사각형에서는 네 변의 중점을 연결하면 평행사변형이 만들어지고, 사다리꼴에서는 윗변과 아랫변의 길이의 평균이 중점연결선의 길이가 됩니다. 이 글에서는 이러한 중점연결정리를 각 도형별로 증명과 함께 정리하고, 실제 값을 구하는 예제 풀이까지 담았습니다.
목차
삼각형의 중점연결정리
- 삼각형의 두 변의 중점을 연결한 선분은 나머지 한 변과 평행하고, 그 길이는 나머지 한 변의 길이의 $\dfrac{1}{2}$이다.
$\triangle ABC$에서 $\overline{AM} = \overline{MB}$, $\overline{AN} = \overline{NC}$이면
$\overline{MN} \pa \overline{BC}$이고 $\overline{MN} = \dfrac{1}{2}\overline{BC}$
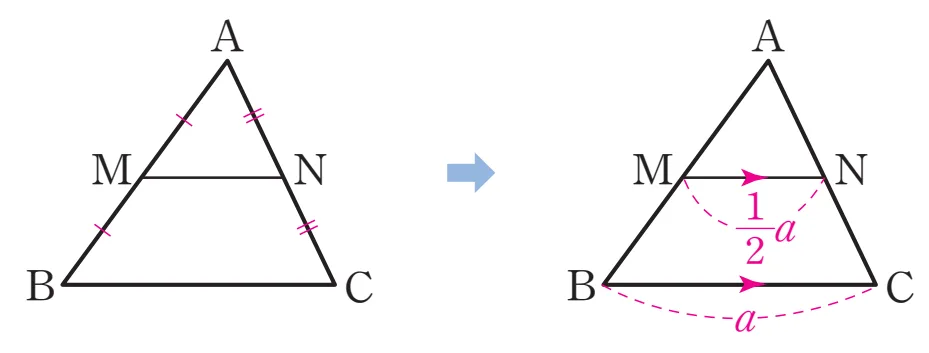
증명
$\triangle AMN \sm \triangle ABC$(SAS 닮음)이고 닮음비가 $1:2$ 이므로 $\overline{MN} \pa \overline{BC}$이고 $\overline{MN} = \dfrac{1}{2}\overline{BC}$
- 삼각형의 한 변의 중점을 지나고 다른 한 변에 평행한 직선은 나머지 한 변의 중점을 지난다.
$\triangle ABC$에서 $\overline{AM} = \overline{MB}$, $\overline{MN} \pa \overline{BC}$이면
$\overline{AN} = \overline{NC}$ 이고
추가로 $\overline{MN} = \dfrac{1}{2}\overline{BC}$도 성립.
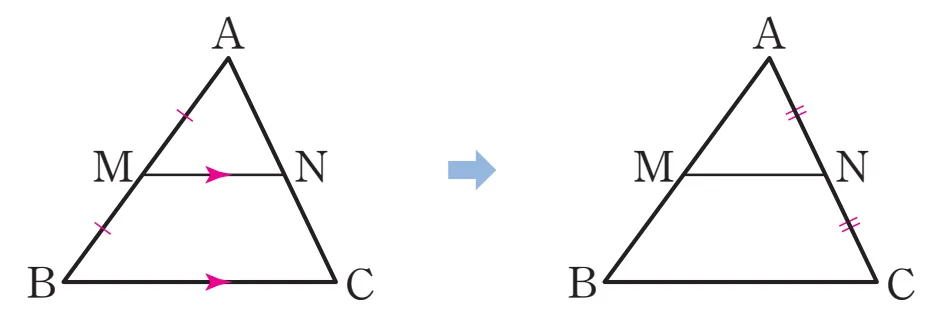
증명
$\triangle AMN \sm \triangle ABC$(AA 닮음)이고, 닮음비가 $1:2$이므로 $\overline{AN} = \overline{NC}$이고 $\overline{MN} = \dfrac{1}{2}\overline{BC}$이다.
예제
오른쪽 그림과 같은 $\triangle ABC$에서 점 M은 $\overline{AB}$의 중점이고 $\overline{MN} \pa \overline{BC}$이다. $\overline{AC} = 12,\mathrm{cm}$, $\overline{BC} = 16,\mathrm{cm}$일 때 $x+y$의 값을 구하시오.
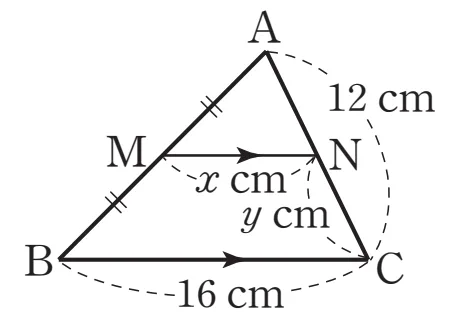
풀이
$\overline{AM} = \overline{MB}$, $\overline{MN} \pa \overline{BC}$이므로
$y = \overline{AN} = \dfrac{1}{2}\overline{AC}$, $y= \dfrac{1}{2} \times 12 = 6$
$x = \dfrac{1}{2}\overline{BC}$, $x=\dfrac{1}{2} \times 16 = 8$
따라서 $x + y = 8 + 6 = 14$
사각형의 중점연결정리
- 모든 사각형의 네 변의 중점을 연결하면 두 쌍의 대변이 각각 평행하므로 평행사변형이 된다.
$\square ABCD$의 네 변의 중점을 각각 P, Q, R, S라 하면
- $\overline{PS} \pa \overline{BD} \pa \overline{QR}$, $\overline{PQ} \pa \overline{AC} \pa \overline{SR}$
- $\overline{PS} = \overline{QR} = \dfrac{1}{2}\overline{BD}$, $\overline{PQ} = \overline{SR} = \dfrac{1}{2}\overline{AC}$
- $\square PQRS$의 둘레의 길이는 $\overline{AC} + \overline{BD}$
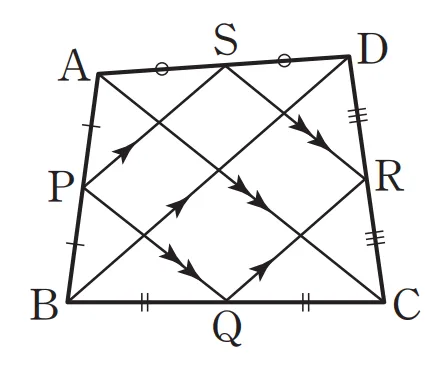
사각형의 중점을 연결한 사각형
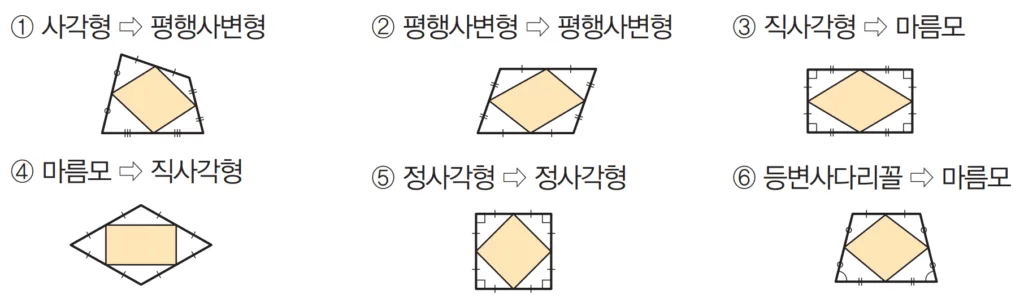
- 위의 증명을 통해 일반적인 사각형의 중점을 연결하면 항상 평행사변형이 됨을 알 수 있습니다.
- 직사각형의 경우 중점을 연결하고 남은 네 직각삼각형이 SAS합동이므로 중점을 연결하면 마름모가 만들어 집니다.
- 마름모의 경우 중점을 연결하고 남은 이등변삼각형의 꼭지각을 이등분하면 8개의 직각삼각형이 모두 합동이 되고 중점을 연결한 사각형은 직사각형이 됩니다.
사다리꼴의 중점연결정리
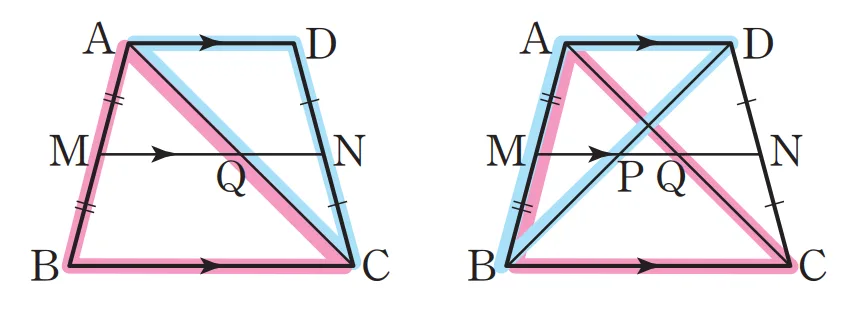
$\overline{AD} \pa \overline{BC}$인 사다리꼴 $ABCD$에서 $\overline{AB}$, $\overline{DC}$의 중점을 각각 M, N이라 하면
- $\overline{AD} \pa \overline{MN} \pa \overline{BC}$
- $\overline{MQ} = \overline{NP} = \dfrac{1}{2}\overline{BC}$, $\overline{MP} = \overline{NQ} = \dfrac{1}{2}\overline{AD}$
- $\overline{MN} = \overline{MQ} + \overline{QN} = \dfrac{1}{2}(\overline{AD} + \overline{BC})$
- $\overline{PQ} = \overline{MQ} – \overline{MP} = \dfrac{1}{2}(\overline{BC} – \overline{AD})$ (단, $\overline{BC} > \overline{AD}$)
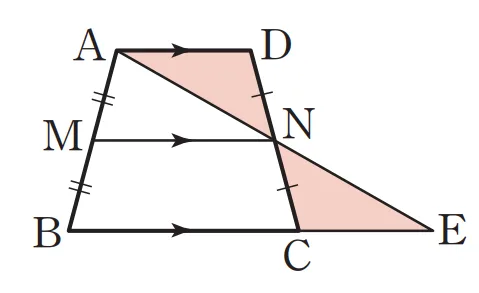
증명1
$\overline{AB}$, $\overline{DC}$의 중점을 각각 M, N이라 하면
$\triangle AND \sm \triangle ENC$(ASA합동)이고 $\overline{AN} = \overline{EN}$
$\triangle ABE$에서 두 변의 중점을 연결한 선분 $\overline{MN}$은 다음을 만족합니다. $\overline{MN} \pa \overline{BE}$
따라서 $\overline{AD} \pa \overline{MN} \pa \overline{BC}$
예제
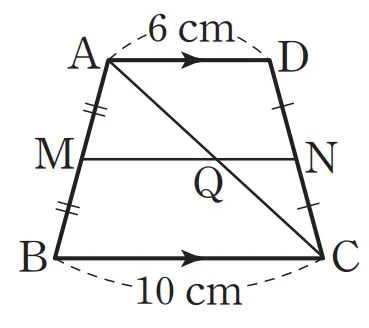
오른쪽 그림과 같이 $\overline{AD} \pa \overline{BC}$인 사다리꼴 $ABCD$에서 점 M, N은 각각 $\overline{AB}$, $\overline{DC}$의 중점이다.
$\overline{AD} = 6,\mathrm{cm}$, $\overline{BC} = 10,\mathrm{cm}$일 때 $\overline{MN}$의 길이를 구하시오.
풀이
중점연결정리에 의해 $\overline{AD} \pa \overline{MN} \pa \overline{BC}$이므로
$\overline{MQ} = \dfrac{1}{2}\overline{BC} = \dfrac{1}{2} \times 10 = 5$
$\overline{QN} = \dfrac{1}{2}\overline{AD} = \dfrac{1}{2} \times 6 = 3$
따라서 $\overline{MN} = \overline{MQ} + \overline{QN} = 5 + 3 = 8cm$
[출처: 개념원리]
