작도는 눈금없는 자와 컴퍼스를 이용해 도형을 그리는 방법입니다. 이 방법은 삼각형을 이해하는데 유용합니다. 이번 시간에는 기본 도형의 작도를 이용해 삼각형을 작도 해보고, 삼각형의 결정조건에 대해 정리해 보도록 하겠습니다.
목차
기본 도형의 작도
작도: 눈금없는 자와 컴퍼스만을 이용해 도형을 그리는것
- 눈금없는 자 : 두 점을 연결, 선을 연장할 때 사용
- 컴퍼스 : 원을 그릴 때, 길이를 옮길 때
선분과 각의 작도
길이가 같은 선분의 작도
작도에서 선분은 길이를 재서 옮기지 않고 컴퍼스를 이용해 옮긴다.
$\overline{AB}$와 길이가 같은 $\overline{PQ}$를 작도하는 과정은 다음과 같다.

- 자로 직선을 그리고 직선 위에 $\bbox[#ffff00]{\text{기준점}}$ $P$를 찍는다.
- 컴퍼스로 $\overline{AB}$의 길이를 잰다.
- 점 $P$를 중심으로 하고 반지름이 $\overline{AB}$인 원을 그려 교점을 $Q$로 두면 $\overline{AB}=\overline{PQ}$
크기가 같은 각의 작도
$\angle{AOB}$와 크기가 같은 각을 오른쪽 반직선 상에 작도하는 방법은 다음과 같다.

- $O$를 중심으로 $\bbox[#ffff00]{\text{기준원}}$을 그리고 $\overrightarrow{OA},\;\overrightarrow{OB}$와 만나는 점을 각각 $C,\;D$라 하자.
- $P$를 중심으로 $\bbox[#ffff00]{\text{기준원}}$을 그리고 $\overrightarrow{PQ}$와 만나는 점을 $X$라고 하자.
- 컴퍼스를 이용해 $\overline{CD}$의 길이를 측정한다.
- $X$를 중심으로 반지름이 $\overline{CD}$인 원과 $\bbox[#ffff00]{\text{기준원}}$이 만나는 점을 $Y$라고 하자.
- 자를 이용해 $\overrightarrow{PY}$를 그리면 $\angle{AOB}=\angle{XPY}$이다.
평행선의 작도
직선 $l$과 평행하고 직선 밖의 한 점 $P$를 지나는 평행한 직선을 작도하는 방법은 다음과 같다.

- 점 $P$를 지나는 직선과 $l$의 교점을 $Q$라고 하자.
- 직선 $l$과 $\overleftrightarrow{PQ}$의 교각과 크기가 같은 각을 점 $P$에 동위각 자리에 작도한다.
삼각형의 작도
삼각형의 명칭과 용어
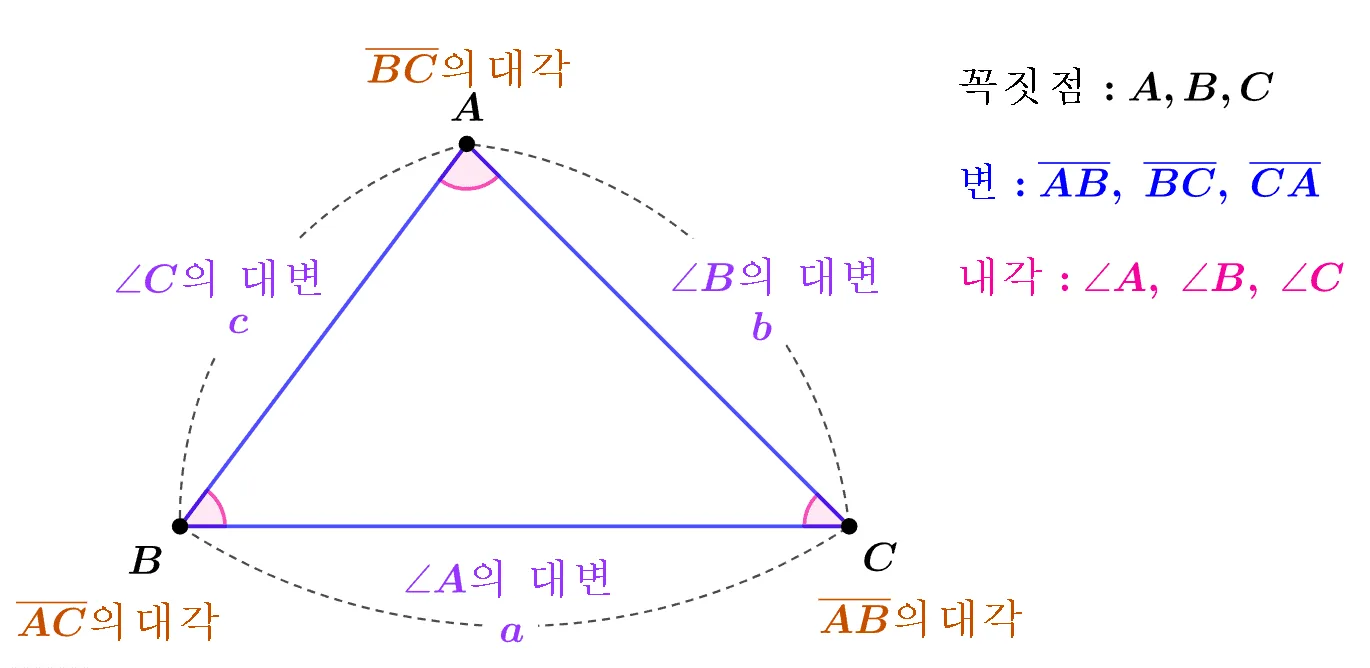
삼각형 $ABC$ : 일직선 상에 있지 않은 세 점 $A,\;B,\;C$를 선분으로 연결한 평면도형.
- 기호 : $\triangle{ABC}$
- 삼각형의 넓이를 의미하기도 한다.
- 명칭
- 꼭짓점 : 점 $A,\;B,\;C$
- 변 : $\overline{AB},\;\overline{BC},\;\overline{CA}$
- 내각 : $\angle{A},\;\angle{B},\;\angle{C}$
- 용어 : 대변과 대각의 ‘대’는 한자로 ‘對:마주할 대’이고 용어는 다음과 같이 사용한다.
- $\angle{A}$의 대변 : $\overline{BC}$
- 일반적으로 대변의 길이는 꼭짓점의 소문자 사용
- $\overline{AB}$의 대각 : $\angle{C}$
- $\angle{A}$의 대변 : $\overline{BC}$
삼각형의 작도
삼각형은 변과 각이 주어지면 그릴 수 있다. 다음의 조건을 이용해 삼각형을 작도해보고 삼각형을 그리기 위한 최소조건 (삼각형의 결정조건)에 대해 정리해 보자.
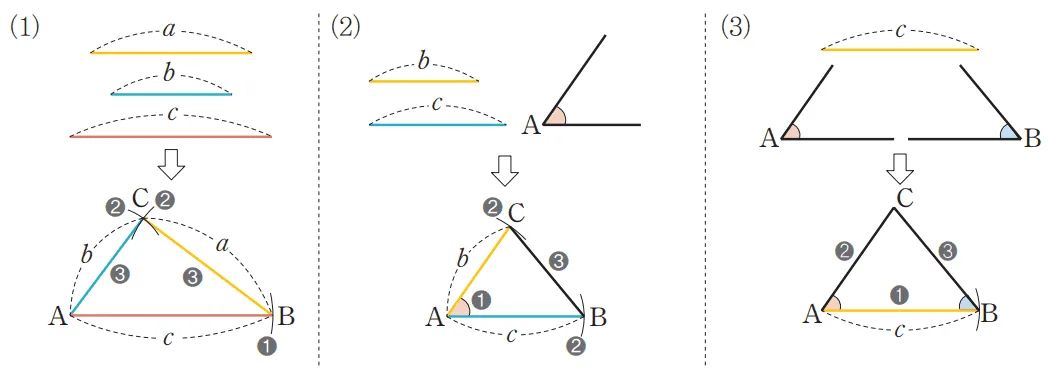
- 세 변의 길이가 주어질 때
- 길이가 $c$인 선분을 작도하여 $\overline{AB}$로 둔다.
- 꼭짓점 $A$에 $\angle{B}$의 대변 ($b$), 꼭짓점 $B$에 $\angle{A}$의 대변 ($a$)을 작도 하여 만나는 교점을 $C$로 둔다.
- $\overline{AC},\;\overline{BC}$를 그린다.
- 두 변의 길이와 끼인각의 크기가 주어질 때
- $\angle{A}$를 작도.
- 두 반직선 위에 길이가 $b,\;c$인 선분을 작도하고, 대각을 고려해 꼭짓점에 $B,\;C$기호를 붙인다.
- $\overline{BC}$를 그린다.
- 한 변과 양 끝각이 주어질 때
- 길이가 $c$인 선분을 작도하여 $\overline{AB}$로 둔다.
- 점 $A,\;B$에서 각각 $\angle{A},\; \angle{B}$를 작도하고 반직선이 만나는 교점을 $C$로 둔다.
- $\overline{AC},\;\overline{BC}$를 그린다.
삼각형의 결정조건 추론
위의 삼각형의 작도 과정을 토대로 삼각형을 결정하는 최소 조건에 대하여 추측해 보면 다음과 같다.
- 세 변의 길이
- 두 변의 길이 + 한 각의 크기
- 한 변의 길이 + 두 각의 크기
- 세 각의 크기
각각의 경우에 대해 삼각형이 결정되지 않는 상황에 대해 살펴 보자.
삼각형이 결정되지 않는 경우
세 변의 길이가 주어진 경우
세 변의 길이가 다음과 같은 삼각형을 작도해 보자.
- $3cm,\;6cm,\;10cm$
- $5cm,\;4cm,\;9cm$

위의 예시를 토대로 세 변의 길이에 다음과 같은 조건이 추가로 필요함을 알 수 있다.
- (최대길이)$<$(나머지 길이 합)
두 변의 길이와 한 각의 크기가 주어진 경우
다음의 조건을 이용해 삼각형을 작도해 보자.
- $\overline{AB}=7cm,\;\overline{AC}=5cm,\;\angle{B}=30^\circ$

위의 조건을 작도하면 조건을 만족하는 삼각형이 두 개 존재함을 알 수 있다. 하나로 결정 되지 않은 이유는 주어진 조건이 두 변의 사이의 끼인각이 아니기 때문이다. 따라서 다음과 같이 수정해야 한다.
- 두 변의 길이와 끼인각의 크기
한 변의 길이와 두 각의 크기가 주어진 경우
한 변의 길이와 두 각이 크기가 주어진 다음의 조건에 대해 생각해 보자.
- $5cm,\;30^\circ,\; 60^\circ$
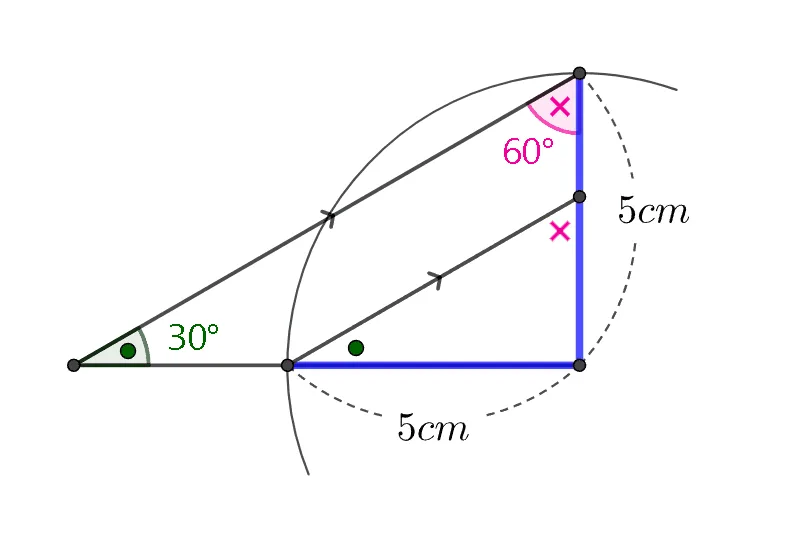
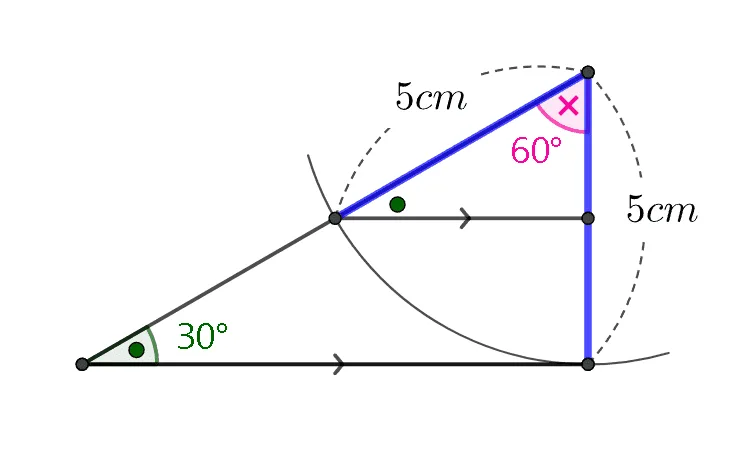
위의 예시를 통해 한 변의 길이와 두 각의 크기가 주어질 때 각의 위치가 결정되어야 함을 알 수 있다. 따라서 결정조건은 다음과 같다.
- 한 변의 길이와 양 끝각의 크기
- (양 끝각 의 합)$<180^\circ$
당연한 말이지만 삼각형의 내각의 합이 $180^\circ$이므로 주어진 양끝각의 합은 이보다 작아야 한다.
세 각의 크기가 주어진 경우
다음의 조건이 주어진 경우에 대해 생각해 보자.
- $30^\circ,\; 60^\circ,\;90^\circ$

위와 같은 이유로 세 각의 크기가 주어진 경우도 삼각형이 유일하게 결정 되지 않는다. 두 각이 주어지면 나머지 한 각은 자동을 결정되기 때문에 실제로 이 조건은 두 각만 주어진 경우와 같다.
앞서 정리한 사실에 따르면 이 조건은 각 사이의 한 변의 길이가 추가로 주어져야 삼각형이 하나로 결정된다.
삼각형의 결정조건
삼각형이 하나로 결정될 조건은 다음과 같다.
- 세 변의 길이가 주어진 경우
- (최대 길이)$<$(나머지 합)
- 두 변의 길이와 끼인각의 크기
- 한 변의 길이와 양 끝각의 크기
- (양 끝각의 합)$<180^\circ$
맺음말
작도는 도형을 그리는 방법을 넘어서 기하학을 탐구하는 중요한 도구입니다. 삼각형이 하나로 결정되기 위한 조건을 확실히 이해하는 시간이 되었기를 바랍니다.
