일차함수 $y = ax + b$는 중학교 수학의 핵심 중 하나입니다. 하지만 단순한 공식 외우기로는 그래프를 정확하게 그리기 어렵고, 기울기와 절편이 어떤 의미인지 헷갈리는 경우가 많습니다. 이 글에서는 복습이 필요한 학생들을 위해 기울기, 절편의 의미로부터 관계식 구하기까지 단계별로 정리했습니다. 특히 그래프 그리는 요령과 관계식 구하는 방법을 실전 예시와 함께 설명하였습니다.
목차
$y=ax+b$ 그래프, 기울기, 절편(복습)
$y=ax+b$ 그래프
$y=ax+b,\;(a\neq0)$의 그래프는 $y=ax$의 그래프를 위쪽으로 평행이동한 그래프이고, 다음과 같이 학습하였습니다.
- $y=ax\xrightarrow[]{\bbox[#ffff00]{y}\text{축} \bbox[#dcff8c]{b} \text{만큼 평행이동}}y=ax+\bbox[#ffff00]{b}$ ($a\neq0$)
$y=ax+b$ 기울기와 절편
- 일반형: $y=\bbox[#ffff00]{a}x+\bbox[#dcff8c]{b},\; (a\neq0)$
- $\bbox[#ffff00]{\text{기울기}}$: $\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}=\bbox[#ffff00]{a}$
- 절편
- $\bbox[#dcff8c]{y \text{ 절편}}$: $\bbox[#dcff8c]{b}$ ($x=0$)
- $x$ 절편: $-\dfrac{b}{a}$ ($y=0$)
직선의 결정조건(복습)
일차함수는 직선이기 때문에 직선을 결정하기 위한 최소 조건이 주어지면 일차함수도 하나로 결정됩니다. 1학년에 배운 직선의 결정 조건에 대해 정리하고 이를 이용해 일차함수 그래프를 그리는 방법에 대해 정리해 봅시다.
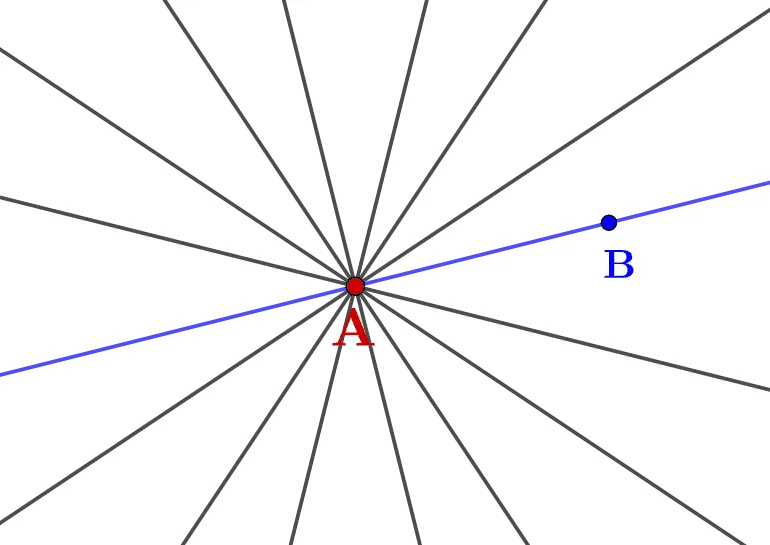
- 직선의 결정조건 (최소 조건)
- 두 점이 주어진 경우
- 한 점과 기울기가 주어진 경우
직선의 결정조건에 대한 글은 아래의 링크를 참고해 주세요.
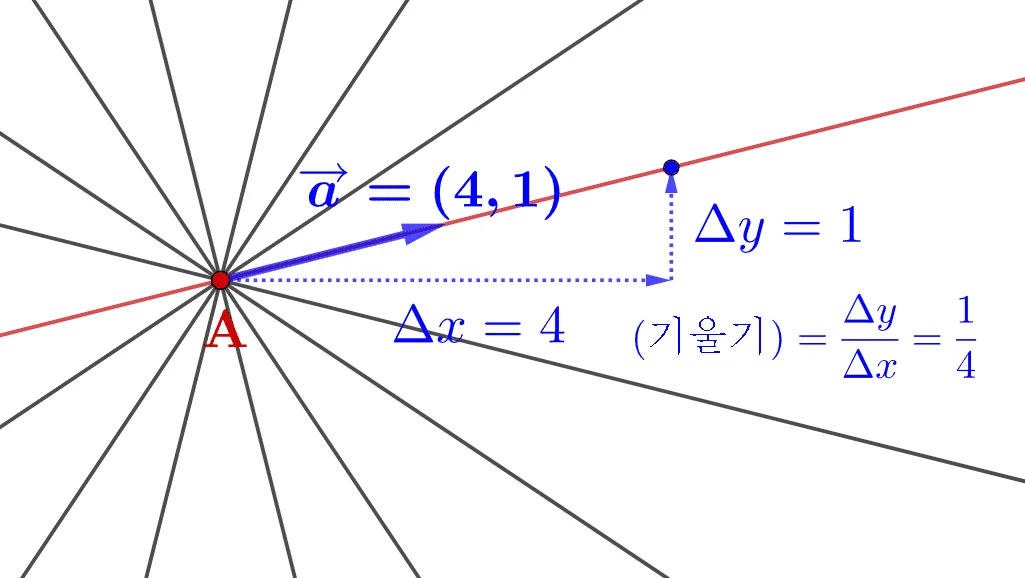
그래프를 이용한 기울기 계산
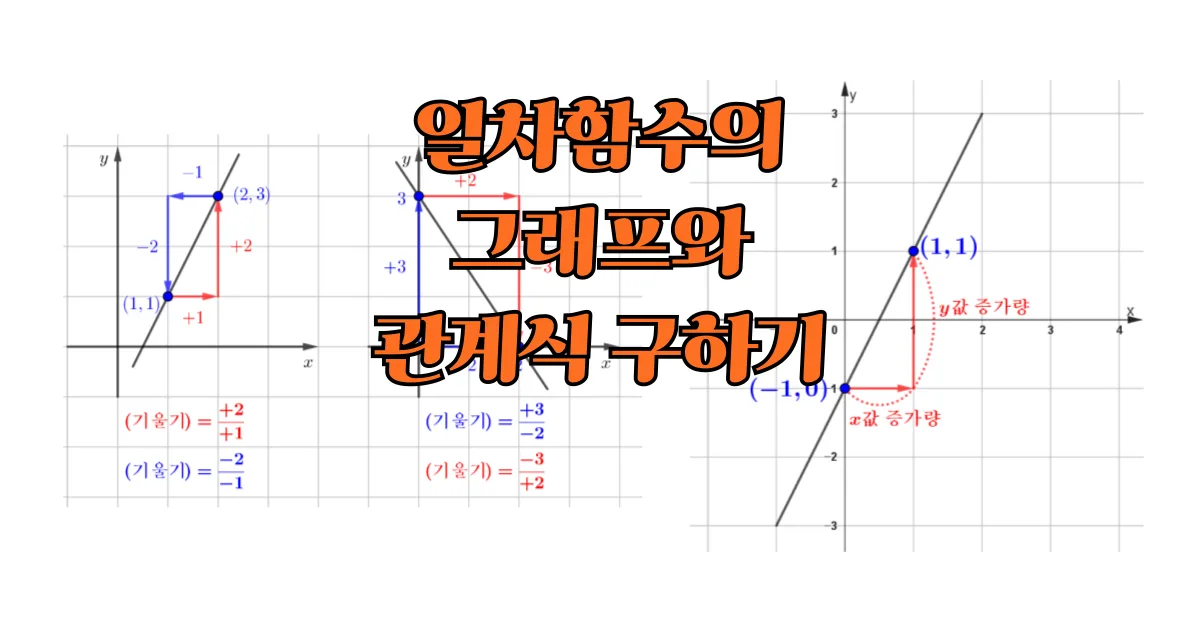
일차함수의 기울기는 $\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}$으로 계산할 수 있습니다. 좌표로 생각하고 계산하지 않고, 그래프에서 기울기를 계산하는 방법에 대해 다음의 예시를 통해 정리해 봅시다.
- $x$값의 증가량
- $x$축의 오른쪽 방향(+), 왼쪽 방향(-)
- $y$값의 증가량
- $x$축의 위쪽 방향(+), 아래쪽 방향(-)
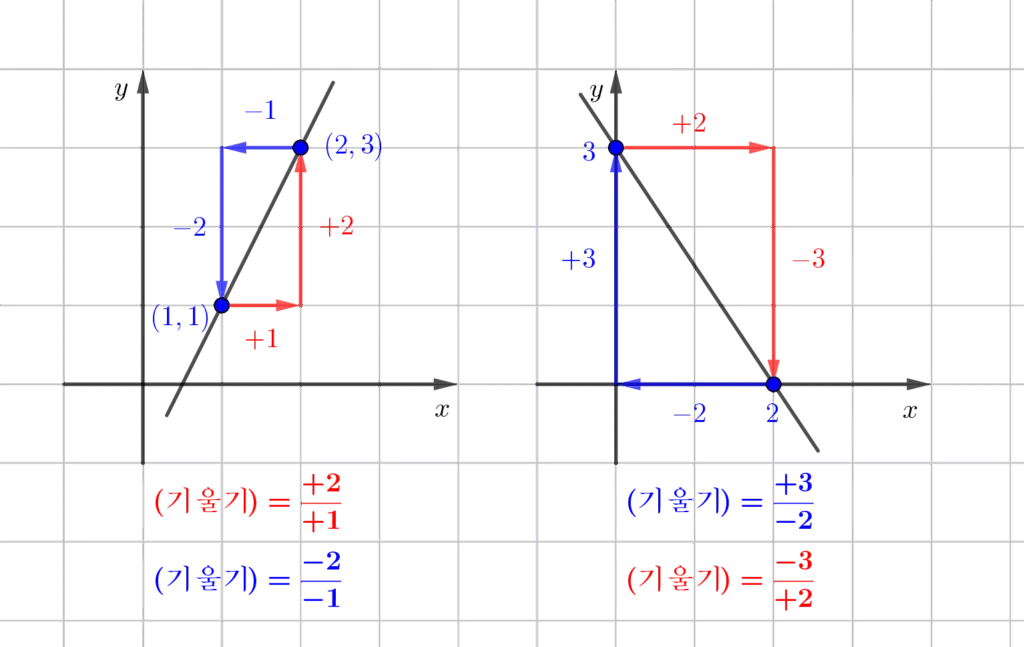
그래프의 증가 감소를 이용하는 방법
- 첫 번째 그래프
- $x$와 $y$의 변화량 비율은 $1:2$ $\rightarrow$ $\pm\dfrac{2}{1}$
- 오른쪽 위로 향하는 직선: $+\dfrac{2}{1}$
- 두 번째 그래프
- $x$와 $y$의 변화량 비율은 $2:3$ $\rightarrow$ $\pm\dfrac{3}{2}$
- 왼쪽 아래로 향하는 직선: $-\dfrac{3}{2}$
관계식으로 그래프 그리기
일차함수의 관계식이 주어졌을 때 그래프를 그리는 방법은 크게 다음과 같고 그래프가 지나는 사분면을 정확하게 파악하려면 점은 $\bbox[#ffff00]{\text{절편}}$을 이용해 선택하는 것이 좋습니다.
- 두 점($\bbox[#ffff00]{\text{절편}}$)을 이용
- 한 점($\bbox[#ffff00]{\text{절편}}$)과 기울기를 이용
두 점을 이용(절편)
두 점을 이용해 $y=\dfrac{1}{2}x-1$의 그래프를 그리는 방법에 대해 살펴봅시다. 관계식을 만족하는 점은 $\cdots$ $(-2,-2),$$(-1,-\dfrac{3}{2}),$$(0,-1),$$(1,-\dfrac{1}{2}),$$(2,0)$ $\cdots$이고 무수히 많은 점이 있습니다. 그래프를 그리기 비교적 정확히 그리기 위해 어떤 점을 선택하는 것이 좋을까요?
그래프의 개형을 파악하기 위해서는 좌표평면상에 두 점의 위치가 비교적 정확해야 합니다. 따라서 정확성을 높이기 위해 좌표축과 만나는 점, 즉 $\bbox[#ffff00]{\text{절편}}$을 이용하는 것이 좋습니다.
주어진 일차함수 $y=\dfrac{1}{2}x\bbox[#ffff00]{-1}$에서 절편을 찾는 방법은 다음과 같습니다.
- $y$ 절편: $x=0$ 일 때 $y=\bbox[#ffff00]{-1}$
- $x$ 절편: $y=0$ 일 때 $x=\bbox[#dcff8c]{2}$
절편을 이용해 $(0,\bbox[#ffff00]{-1}),\;(\bbox[#dcff8c]{2},0)$을 지나는 직선을 그리면 보다 정확한 그래프를 그릴 수 있습니다.
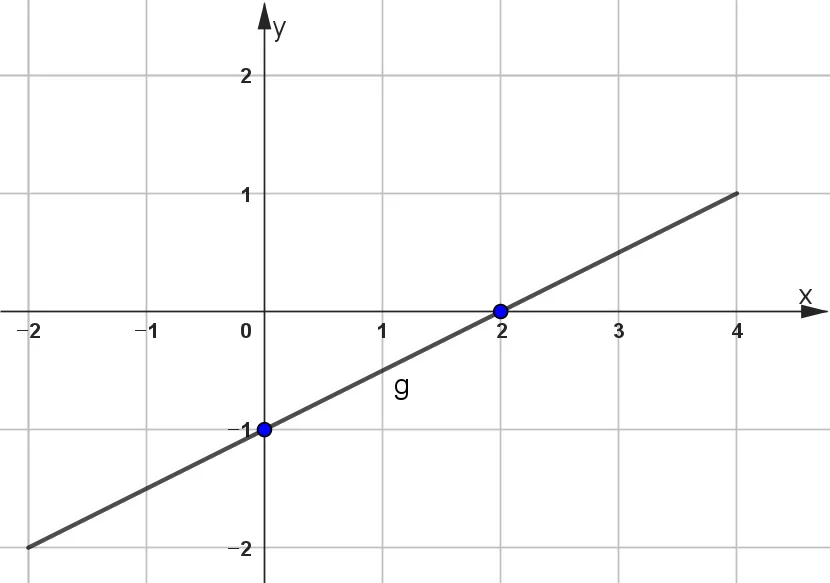
한 점과 기울기를 이용
한 점과 기울기를 이용한 방법에서도 정확도를 높이기 위해 절편을 이용해 한 점을 선택하는 것이 좋습니다. $y=\bbox[#dcff8c]{2}x\bbox[#ffff00]{-1}$에서 한 점과 기울기는 다음과 같이 선택할 수 있습니다.
- 한 점: $y$절편 이용 $\rightarrow$ $(0,\bbox[#ffff00]{-1})$
- 기울기: $\bbox[#dcff8c]{2}$
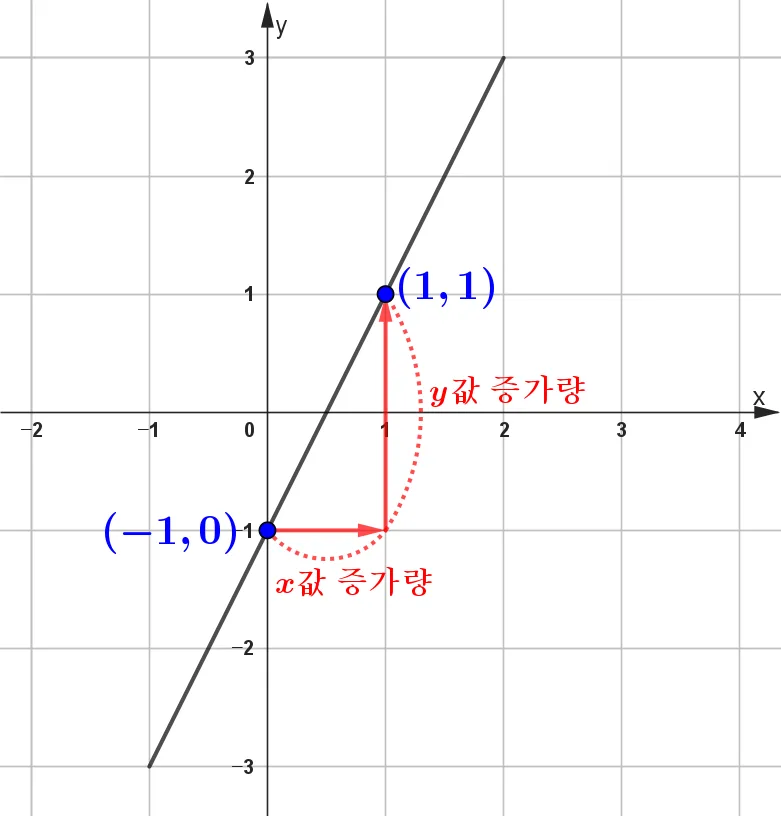
기울기는 $x$의 증가량에 대한 $y$의 증가량의 비율이므로 다음과 같이 해석 할 수 있습니다.
- $\dfrac{\color{red}y\text{값의 증가량}}{\color{blue}x\text{값의 증가량}}=\bbox[#dcff8c]{\dfrac{\color{red}2}{\color{blue}1}}$
따라서 $y=\bbox[#dcff8c]{2}x\bbox[#ffff00]{-1}$은 $(0,\bbox[#ffff00]{-1})$을 지나고, $x$가 $\color{blue}1$증가할 때 $y$가 $\color{red}2$증가한 점$(1,1)$을 지나는 직선을 그리면 됩니다.
일차함수 관계식 구하기
조건에 따라 일차함수의 관계식을 구하는 방법에 대해 살펴봅시다. 이 과정도 직선의 결정 조건에 따라 두 가지 유형으로 나누어 정리할 수 있습니다.
- 기울기와 한 점이 주어진 경우
- 기울기와 $y$절편이 주어진 경우
- 기울기와 한 점이 주어진 경우
- 두 점이 주어진 경우
- 두 점이 주어진 경우
- 두 절편이 주어진 경우
기울기와 한 점이 주어진 경우
한 점이 $y$절편으로 주어진 경우와 $y$절편이 아닌 한 점이 주어진 경우로 나누어 살펴 봅시다.
- 한 점이 $y$절편으로 주어진 경우
- $y$절편이 아닌 한 점이 주어진 경우
1. 기울기와 $y$절편
기울기가 $a$이고 $y$절편이 $b$인 일차함수 관계식은 $y=ax+b$이므로 기울기가 $2$이고 $y$절편이 $-4$인 일차함수의 관계식은 다음과 같습니다.
- $y=ax+b$ $\xrightarrow[y\text{절편}:\;-4\quad]{\text{기울기}:\;2\quad}$ $y=2x-4$
2. 기울기와 $y$절편이 아닌 한 점
한 점 $(-2,9)$를 지나고 기울기가 $\bbox[#ffff00]{-4}$ 인 일차함수 관계식을 구하는 과정에 대해 정리해 봅시다.
먼저 기울기가 $\bbox[#ffff00]{-4}$인 일차함수 관계식은 다음과 같습니다.
- $y=\bbox[#ffff00]{-4}x+b$
위의 관계식에 점 $(-2,9)$를 대입하여 정리하면 $9=\bbox[#ffff00]{-4}\times(-2)+b$이고 $\therefore\; b=1$ 이므로, 일차함수 관계식은 $y=\bbox[#ffff00]{-4}x+1$입니다.
두 점이 주어진 경우
두 점이 주어진 경우는 절편이 주어진 경우와 절편이 아닌 두 점이 주어진 경우로 나누어 정리할 수 있습니다.
- 두 절편이 주어진 경우
- 절편이 아닌 두 점이 주어진 경우
1. 두 절편이 주어진 경우
$x$절편이 $-3$, $y$절편이 $2$인, 일차함수 관계식을 구하는 과정에 대해 정리해 봅시다. 절편을 통해 일차함수 위의 두 점을 $(-3,0),(0,2)$를 이용해 다음과 같이 풀이할 수 있습니다.
방법1. 연립방정식 이용
일차함수 $y=ax+b$가 두 점을 $(-3,0),(0,2)$을 지나므로 연립방정식을 다음과 같이 세울 수 있습니다.
$\begin{cases} 0=-3a+b\\2=b\end{cases}$
$\therefore\; a=\dfrac{2}{3},\;b=2$ 이고 관계식은 $y=\dfrac{2}{3}x+2$입니다.
방법2. 기울기와 y절편 이용
두 점을 $\bbox[#ffff00]{(-3,0)},\bbox[#dcff8c]{(0,{\color{red}2})}$을 지나는 직선의 기울기와 $y$절편은 다음과 같습니다.
- 기울기: $\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}=\dfrac{\bbox[#dcff8c]{2}-\bbox[#ffff00]{0}}{\bbox[#dcff8c]{0}-(\bbox[#ffff00]{-3})}={\color{blue}\dfrac{2}{3}}$
- $y$절편: $\color{red}2$
따라서 일차함수 관계식은 $y={\color{blue}\dfrac{2}{3}}x+{\color{red}2}$입니다.
절편을 이용한 일차함수식 (공식)
아래의 공식은 암기해야 하는 식이 아닙니다. 주어진 조건을 이용해 바로 공식을 유도할 수 있도록 과정을 익히는 것이 중요합니다.
$x$절편이 $m$이고 $y$절편이 $\bbox[#ffff00]{n}$인 일차함수의 관계식을 구하는 식은 다음과 같이 유도할 수 있습니다.
- $(m,0),\;(0,n)$을 지나는 직선의 기울기
- $(\text{기울기})=\dfrac{n-0}{0-m}=-\dfrac{n}{m}$
따라서 일차함수식은 $y=-\dfrac{n}{m}x+\bbox[#ffff00]{n}$입니다.
2. 절편이 아닌 두 점이 주어진 경우
$(-2,-1),\;(1,5)$를 지나는 일차함수 관계식을 구하는 방법에 대해 살펴봅시다.
방법1. 연립방정식 이용
일차함수의 관계식을 $y=ax+b$이라 두고 $(-2,-1),\;(1,5)$을 대입
$\begin{cases}-2a+b=-1\cdots(ㄱ)\\a+b=5\cdots(ㄴ)\end{cases}$
$\begin{align}\quad&-2a+b=-1\\
-)&\quad \;\; a+b=5\\
\hline
\quad& -3a=-6\end{align}$
$\therefore \; a=2,\; b=3$ 이고 일차함수 관계식은 $y=2x+3$입니다.
방법2. 기울기 이용
$\bbox[#ffff00]{(-2,-1)},\;\bbox[#dcff8c]{(1,5)}$을 지나는 일차함수 $y=\bbox[#94feff]{a}x+b$의 기울기($\bbox[#94feff]{a}$)는 다음과 같이 구할 수 있습니다.
$\bbox[#94feff]{a}=\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}=\dfrac{\bbox[#dcff8c]{5}-(\bbox[#ffff00]{-1})}{\bbox[#dcff8c]{1}-(\bbox[#ffff00]{-2})}=\bbox[#94feff]{2}$
$y=\bbox[#94feff]{2}x+b$에 $(1,5)$를 대입하면 $b=3$이고 따라서 관계식은 $y=2x+3$입니다.