이번 시간에는 이차함수의 축과 꼭짓점을 구하는 방법에 대해 살펴보기로 하자. 먼저 평행이동을 이용한 방법을 생각하고 다음으로 완전제곱식의 대칭성을 이용한 이차함수 대칭축을 찾는 방법에 대해 알아보기로 하자.
목차
학습목표
- $y=a(x-p)^2+q$의 축과 꼭짓점을 구하는 과정을 평행이동을 이용해 설명 할 수 있다.
- $y=a(x-p)^2+q$의 축과 꼭짓점을 완전제곱식의 대칭성을 이용해 구할 수 있다.
이번시간 학습에 들어가기 전 $y=ax^2 \; (a\neq0)$ 으로 주어진 이차함수의 그래프 성질이 생각나지 않는다면 아래의 복습 링크로 가서 학습을 정리하고 오길 바란다.
이차함수의 축과 꼭짓점
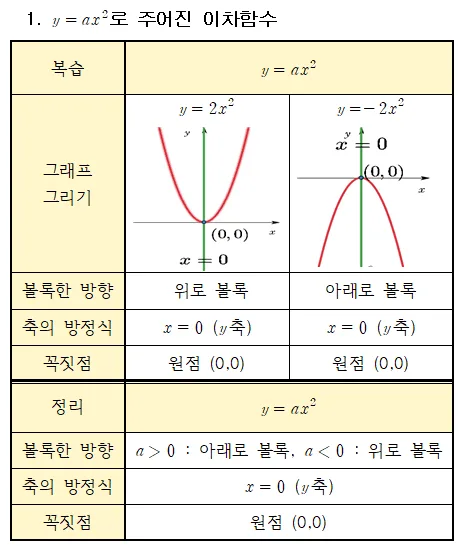
$y=ax^2$의 그래프 성질
전에 다룬 내용에서 축과 꼭짓점 그래프의 개형에 대한 내용을 정리하면 다음과 같다.
$y=ax^2$ 축과 꼭짓점
- 축과 축의 방정식 : 축은 $y$축이고 축의 방정식은 $x=0$이다.
- 꼭짓점 : $(0,0)$
$y=ax^2$ 그래프의 개형
$y=a(x-p)^2+q$ 의 축과 꼭짓점
전 시간에 $y=a(x-p)^2+q$ 은 $y=ax^2$을 $x$축으로 $p$, $y$축으로 $q$만큼 평행이동한 그래프라는 사실을 학습하였다. 확실하게 설명할 수 없다면 다음 링크를 통해 복습하고 오길 바란다.
문제를 통해 $y=a(x-p)^2+q$의 그래프를 $y=ax^2$의 평행이동을 사용해 설명하는 방법을 학습하고, 축의 방정식과 꼭짓점의 좌표를 구하는 방법에 대해 알아보자.
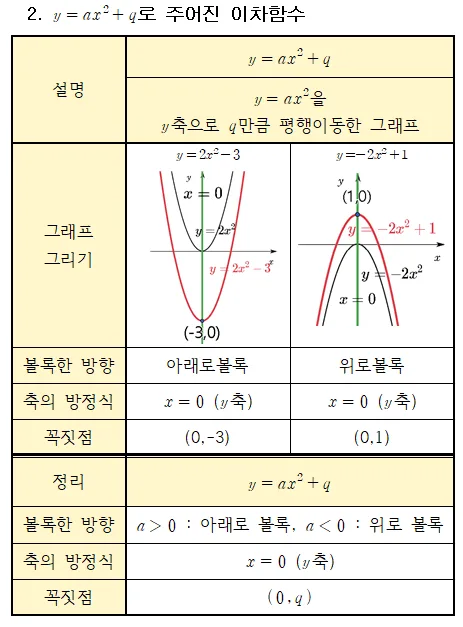
$y=ax^2+q$의 축 꼭짓점
예시를 통해 $y$축 평행이동과 축과 꼭짓점의 이동에 대해 학습해 보기로 하자.
예시 $y=2x^2-3$의 그래프
이 그래프는 $y=2x^2$을 $y$축으로 $-3$만큼 평행이동한 그래프 이다. 따라서 축의 방정식과 꼭짓점은 다음과 같이 이동한다.
- 축의 방정식 : $x=0$, $y$축
- 꼭짓점의 좌표 : $(0,-3)$
예시 $y=-2x^2+1$의 그래프
이 그래프는 $y=2x^2$을 $y$축으로 $+1$만큼 평행이동한 그래프 이다. 따라서 축의 방정식과 꼭짓점은 다음과 같이 이동한다.
- 축의 방정식 : $x=0$, $y$축
- 꼭짓점의 좌표 : $(0,+1)$
[정리] $y=ax^2+q$의 평행이동과 축과 꼭짓점의 이동
- $y=ax^2+q$ : $y=ax^2$을 $y$축으로 $q$만큼 평행이동한 그래프
- 축의 방정식 : $x=0$, $y$축
- 꼭짓점의 좌표 : $(0,q)$
학습지 정리
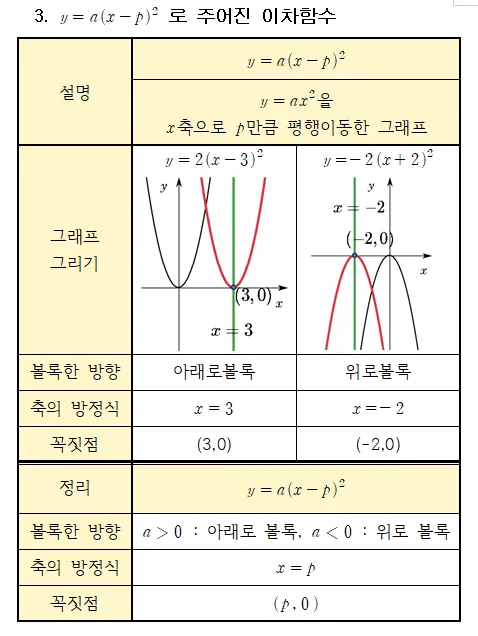
$y=a(x-p)^2$의 축 꼭짓점
위와 동일한 방법으로 예시를 통해 $x$축 평행이동과 축과 꼭짓점의 이동에 대해 학습해 보기로 하자.
예시 $y=2(x-3)^2$의 그래프
이 그래프는 $y=2x^2$을 $x$축으로 $3$만큼 평행이동한 그래프 이다. 따라서 축의 방정식과 꼭짓점은 다음과 같이 이동한다.
- 축의 방정식 : $x=3$
- 꼭짓점의 좌표 : $(3,0)$
예시 $y=-2(x+2)^2$의 그래프
이 그래프는 $y=-2x^2$을 $x$축으로 $-2$만큼 평행이동한 그래프 이다. 따라서 축의 방정식과 꼭짓점은 다음과 같이 이동한다.
- 축의 방정식 : $x=-2$
- 꼭짓점의 좌표 : $(-2,0)$
[정리] $y=a(x-p)^2$의 평행이동과 축과 꼭짓점의 이동
- $y=a(x-p)^2$ : $y=ax^2$을 $x$축으로 $p$만큼 평행이동한 그래프
- 축의 방정식 : $x=p$
- 꼭짓점의 좌표 : $(p,0)$
학습지 정리
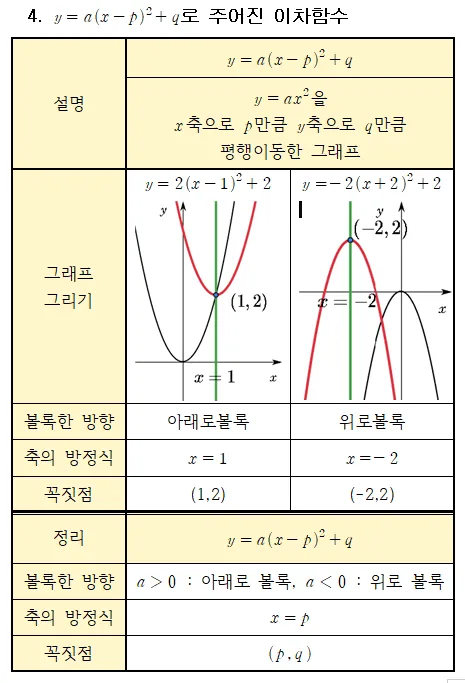
$y=a(x-p)^2+q$의 축 꼭짓점
위와 동일한 방법으로 예시를 통해 $x$축 평행이동과 축과 꼭짓점의 이동에 대해 학습해 보기로 하자.
예시 $y=2(x-1)^2+2$의 그래프
이 그래프는 $y=2x^2$을 $x$축으로 $1$만큼, $y$축으로 $2$만큼 평행이동한 그래프 이다. 따라서 축의 방정식과 꼭짓점은 다음과 같이 이동한다.
- 축의 방정식 : $x=1$
- 꼭짓점의 좌표 : $(1,2)$
예시 $y=-2(x+2)^2+2$의 그래프
이 그래프는 $y=-2x^2$을 $x$축으로 $-2$만큼, $y$축으로 $2$만큼 평행이동한 그래프 이다. 따라서 축의 방정식과 꼭짓점은 다음과 같이 이동한다.
- 축의 방정식 : $x=-2$
- 꼭짓점의 좌표 : $(-2,2)$
[정리] $y=a(x-p)^2+q$의 평행이동과 축과 꼭짓점의 이동
- $y=a(x-p)^2$ : $y=ax^2$을 $x$축으로 $p$만큼, $y$축으로 $q$만큼 평행이동한 그래프
- 축의 방정식 : $x=p$
- 꼭짓점의 좌표 : $(p,q)$
학습지 정리
정리
$y=a(x-p)^2+q$의 축과 꼭짓점
- $y=ax^2$을 $x$축으로 $p$만큼, $y$축으로 $q$만큼 평행이동
- 축의 방정식 : $x=p$
- 꼭짓점의 좌표 : $(p,q)$
지금까지 이차함수 $y=a(x-p)^2+q$의 축과 꼭짓점을 평행이동을 이용해 구하는 방법에 대해 알아 보았다. 식의 성질을 이용해 축과 꼭짓점을 구하는 방법에 대해서도 정리하고 넘어가 보자.
축과 꼭짓점을 구하는 다른 방법
이차함수 $y=a(x-p)^2+q$는 본질적으로 $y=ax^2$과 같은 대칭성을 갖는다는 사실을 이용하면 축을 쉽게 생각할 수 있다. 아래에 제시된 예시의 관계식을 보면서 정리해 보자.
예시 $y=x^2$의 축과 꼭짓점
- $x=1\;,\;x=-1$에서 함숫값이 같다. 이차함수의 대칭성에 의해 축의 방정식은 $x=0$이다.
- 꼭짓점 좌표 : $(x=0 \;일때 \;y=0)$ 이므로 $(0,0)$이다.
예시 $y=(x-3)^2+1$의 축과 꼭짓점
- $(x-3)=1\;,\;(x-3)=-1$에서 함숫값이 같다. 이차함수의 대칭성에 의해 축의 방정식은 $(x-3)=0$ 즉 $x=3$이다.
- 꼭짓점 좌표 : $(x=3\;일때\;y=1)$ 이므로 $(3,1)$이다.
위의 두 예시를 통해 알 수 있는 사실은 완전제곱식으로 정리했을 때 $(완전제곱식)=0$이 되는 $x$값에서 함수가 대칭이 됨을 알 수 있다. 따라서 일반화 하여 정리하면 아래와 같이 축과 꼭짓점을 구할 수 있다.
$y=a(x-p)^2+q$의 축과 꼭짓점
- 축의 방정식 : $(완전제곱)=0$을 만족하는 $x$값 즉 $x=p$
- 꼭짓점의 좌표: $(x=p\;일때\;y=q)$ 이므로 $(p,q)$
마무리 조언
학생들은 평행이동식을 이용해 축과 꼭짓점을 구하는 과정에서 부호 실수를 많이 한다. 이를 개선하기 위해서 완전제곱식의 대칭성을 이용하는 두번째 방법을 익혀서 사용하길 바란다. 이 방법은 식의 구조를 이용하는 방법으로 평행이동에서 발생하는 부호 혼동을 크게 줄일 수 있다.
