이등변삼각형은 겉으로 보면 단순해 보이지만, 수학적인 사고력을 키우는 데 꼭 필요한 개념입니다. 단순히 두 변의 길이가 같다는 특징만 아는 것이 아니라, 그 안에 숨어 있는 정의·성질·조건 사이의 논리적 관계를 이해하는 과정이 기하학적 사고를 확장시키는 핵심 훈련이 됩니다.
특히 이등변삼각형은 중학교 수학에서 ‘증명’의 시작점 역할을 합니다. 밑각의 성질, 각의 이등분선과 수직이등분선의 관계, 중선의 의미 등을 탐구하다 보면, “왜 이런 성질이 성립할까?”, “조건과 정의는 어떻게 연결될까?”와 같은 근본적인 질문에 스스로 답을 찾을 수 있는 힘이 길러집니다.
목차
이등변삼각형의 성질과 조건
중학교 2학년에서는 중학교 1학년 때 배운 이등변삼각형의 성질과 조건에 대한 증명을 자세히 다루게 됩니다. 이등변삼각형의 성질과 조건을 아래의 정의를 이용하여 증명하는 과정에 대해 학습해 봅시다.
- 이등변삼각형의 정의: 두 변의 길이가 같은 삼각형
이등변삼각형의 성질과 조건은 다음과 같이 크게 세가지로 구분할 수 있습니다.
- 밑각의 크기에 대한
- 성질: 이등변삼각형 $\Rightarrow$ 두 밑각의 크기가 같다.
- 조건: 두 각의 크기가 같으면 $\Rightarrow$ 이등변삼각형
- 꼭지각의 이등분선에 대한
- 성질: 이등변삼각형 $\Rightarrow$ 꼭지각의 이등분선이 밑변을 수직이등분 한다.
- 조건: 각의 이등분선이 대변을 수직이등분 하면 $\Rightarrow$ 이등변삼각형
- 밑변의 수직이등분선에 대한
- 성질: 이등변삼각형 $\Rightarrow$ 밑변의 수직이등분선이 꼭지각을 지난다.
- 조건: 한 변의 수직이등분선이 대각을 지나면 $\Rightarrow$ 이등변삼각형
이등변삼각형의 성질 증명
먼저 이등변삼각형의 다음 성질에 대해 증명해 보도록 하겠습니다.
- 이등변삼각형 $\Rightarrow$ 두 밑각의 크기가 같다.
- 이등변삼각형 $\Rightarrow$ 꼭지각의 이등분선이 밑변을 수직이등분 한다.
- 이등변삼각형 $\Rightarrow$ 밑변의 수직이등분선이 꼭지각을 지난다.
밑각의 크기에 대한 성질
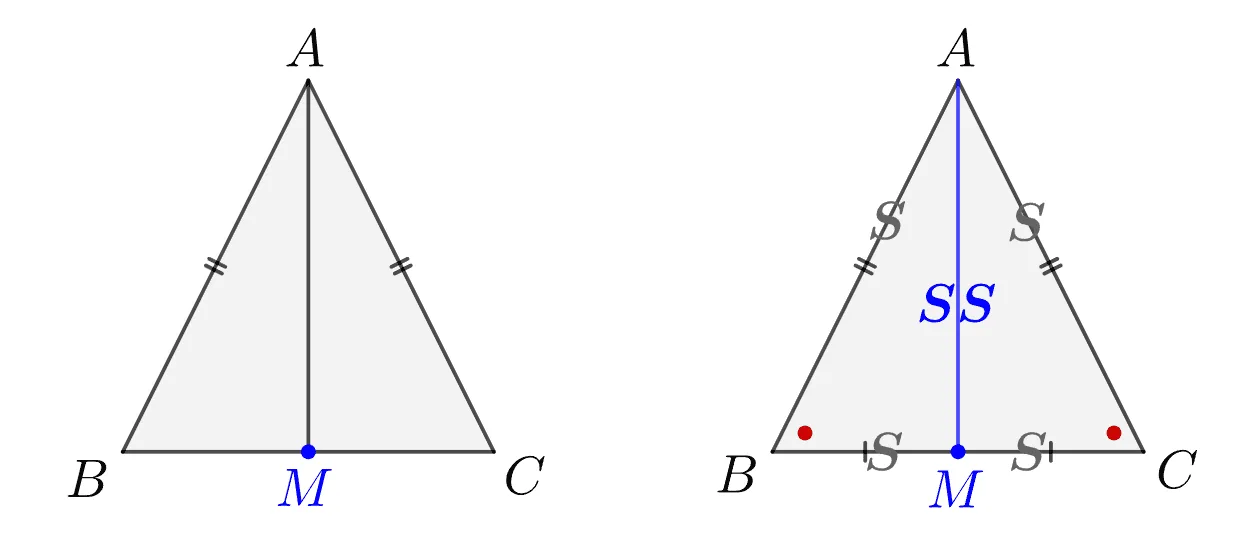
이등변삼각형은 두 변의 길이가 같은 삼각형을 의미하고 아래와 같은 성질을 갖습니다. 이를 증명하는 과정은 다음과 같습니다.
- 성질: 이등변삼각형 $\Rightarrow$ 두 각의 크기가 같다.
[증명]
- 중학교 1학년: 중선(보조선)을 주어진 상태로 성질을 증명
- 중학교 2학년: 보조선이 주어지지 않은 상태에서 증명
$\triangle{ABM}\equiv\triangle{ACM}$ (SSS 합동)
- $\overline{AB}=\overline{AC}$
- $\overline{BM}=\overline{CM}$
- $\overline{AM}\text{ : 공통}$
$\therefore\; \angle{ABM}=\angle{ACM}$
증명의 핵심은 $\overline{BC}$의 중점 $M$에 대해 보조선 $\overline{AM}$을 그리는 것입니다. 중학교 2학년에서는 어떤 보조선 그려야하는지에 대해 생각해 보아야 합니다. 위의 증명은 중선을 선택했지만 각의 이등분선을 선택할 수도 있습니다.
- 중선: 세 변의 길이가 같은 SSS 합동조건을 이용하기 위한 보조선
- 각의 이등분선: 두 변의 길이와 끼인각이 같은 SAS 합동조건을 이용하기 위한 보조선
이등변삼각형의 중선 성질
위의 기본성질을 증명하는 과정에서 $\triangle{ABM}\equiv\triangle{ACM}$ (SSS 합동)임을 이용하면 이등변삼각형에서 다음 선분은 일치함을 알 수 있습니다.
- 꼭지각에서 대변에 그은 중선
- 꼭지각의 이등분선
- 밑변의 수직이등분선
- 꼭지각에서 대변에 내린 수선
꼭지각의 이등분선의 성질
다음의 두 번째 성질에 대해 정리해 봅시다.
- 성질: 이등변삼각형 $\Rightarrow$ 꼭지각의 이등분선이 밑변을 수직이등분 한다.
[증명1]
이 성질은 앞서 정리한 이등변삼각형의 중선 성질을 이용하면 너무 당연한 사실입니다.
- 꼭지각의 이등분선과 밑변의 수직이등분선이 일치한다.
여기서는 중선 성질을 이용하지 않고 합동을 이용해 직접 증명하면서 증명과정을 수식으로 표현하는 연습을 해 봅시다.
[증명2]
이등변삼각형의 꼭지각의 이등분선과 밑변의 교점 $D$에 대하여 다음이 성립합니다.
$\triangle{ABD}\equiv\triangle{ACD}$ (SAS 합동)
- $\overline{AB}=\overline{AC}$
- $\angle{BAD}=\angle{CAD}$
- $\overline{AD}$ 공통
따라서 다음이 성립합니다.
- $\overline{BD}=\overline{CD}$ : $D$는 중점
- $\angle{ADB}=\angle{ADC}=90^\circ$
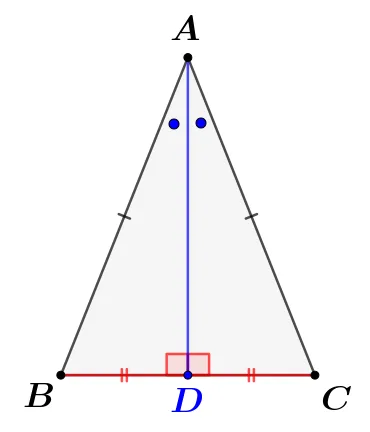
위의 사실을 정리하면 이등변삼각형에서 꼭지각의 이등분선이 밑변을 수직이등분 함을 알 수 있습니다.
밑변의 수직이등분선 성질
밑변의 수직이등분선에 대한 성질과 관련된 조건은 다음과 같습니다.
- 성질: 이등변삼각형 $\Rightarrow$ 밑변의 수직이등분선이 꼭지각을 지난다.
위의 성질은 이등변삼각형의 중선에 대한 성질을 이용해 간단히 증명하고 넘어가도록 하겠습니다.
[증명]
이등변삼각형에서 꼭지각의 이등분선은 다음과 같은 성질을 가지고 있습니다.
- 이등변삼각형에서 꼭지각의 이등분선은 밑변을 수직 이등분한다.
따라서 밑변의 수직이등분선이 꼭지각의 이등분선과 일치하고 다음과 같이 표현할 수 있습니다.
- 밑변의 수직이등분선이 꼭지각을 지난다.
이등변삼각형의 조건 증명
위의 성질을 만족하는 삼각형이 이등변삼각형이 되는를 살펴보아야 합니다.
- 두 각의 크기가 같으면 $\Rightarrow$ 이등변삼각형
- 각의 이등분선이 대변을 수직이등분 하면 $\Rightarrow$ 이등변삼각형
- 변의 수직이등분선이 대각을 지나면 $\Rightarrow$ 이등변삼각형
밑각 조건 증명
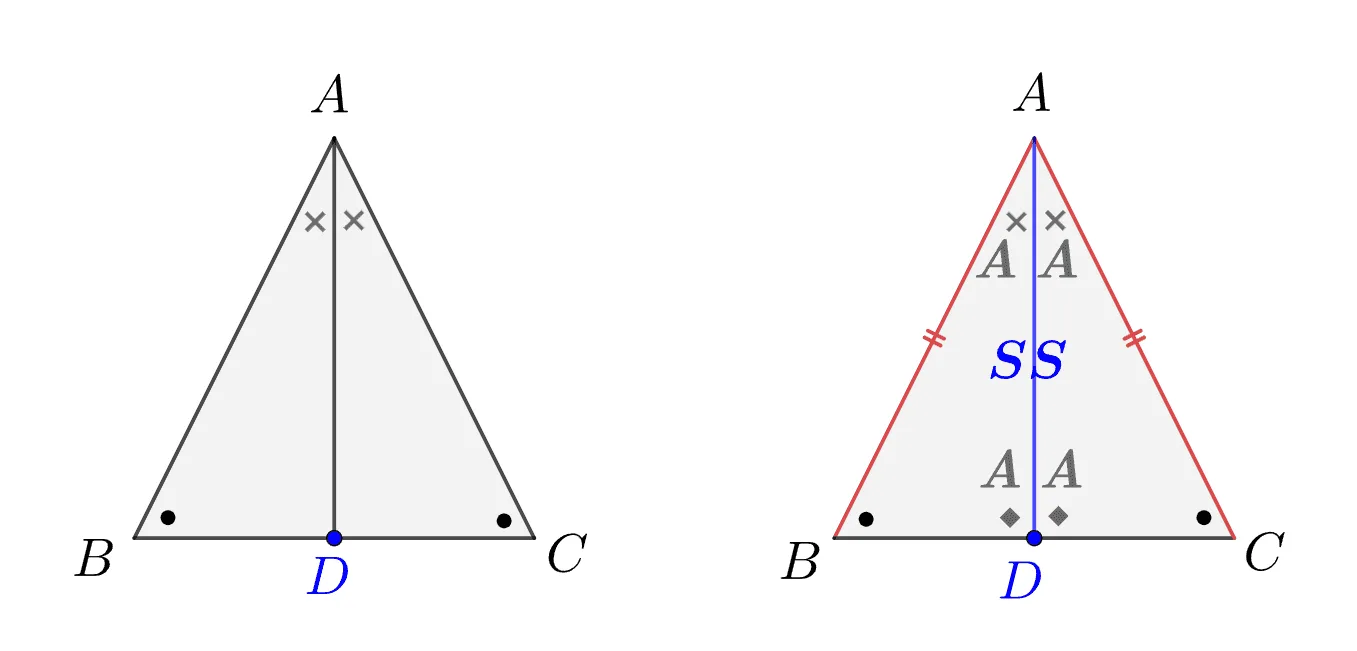
밑각의 성질을 만족하는 것이 이등변삼각형이 되는 조건이 될 수 있는지에 대해 증명해 봅시다.
- 조건: 두 각의 크기가 같으면 $\Rightarrow$ 이등변삼각형
[증명]
- 중학교 1학년: 각의 이등분선(보조선)이 주어진 상태로 증명
- 중학교 2학년: 보조선이 주어지지 않은 상태에서 증명
$\triangle{ABD}\equiv\triangle{ACD}$ (ASA 합동)
- $\angle{BAD}=\angle{CAD}$
- $\angle{ADB}=\angle{ADC}$
- $\overline{AD}\text{ : 공통}$
$\therefore \; \overline{AB}=\overline{AC}$
증명의 핵심은 $\angle{A}$의 이등분선과 $\overline{BC}$의 교점 $D$에 대하여 보조선 $\overline{AD}$를 그리는 것입니다. 이 경우도 각의이등분선을 그리는 이유를 살펴보면 다음과 같습니다.
- 각의 이등분선: 한 변의 길이와 양 끝각이 같은 ASA 합동조건을 이용하기 위한 보조선
각의 이등분선 조건
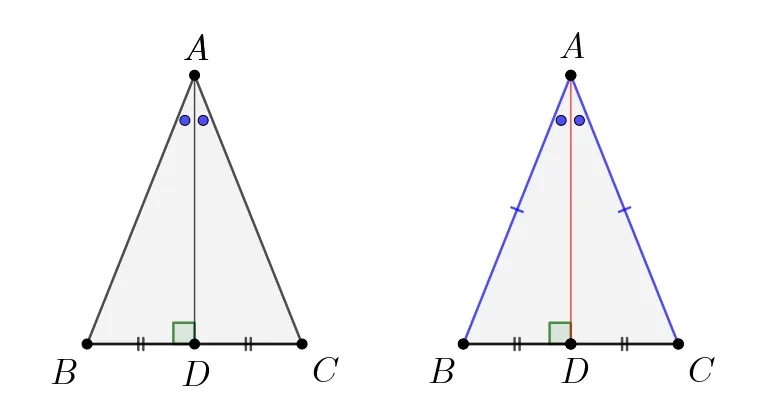
각의 이등분선이 아래와 같은 조건을 만족하면 이등변삼각형이 됩니다.
- 조건: 각의 이등분선이 대변을 수직이등분 하면 $\Rightarrow$ 이등변삼각형
[증명]
각 A의 이등분선이 $\overline{BC}$와 $D$에서 만나고, 대변을 수직이등분하면 아래와 같은 이유로 $\triangle{ABD}\equiv\triangle{ACD}$(SAS 합동)가 성립합니다.
- $\overline{BD}=\overline{CD}$
- $\angle{ADB}=\angle{ADC}=90^\circ$
- $\overline{AD}$: 공통
따라서 $\overline{AB}{\color{blue}=}\overline{AC}$이고 이등변삼각형이 됩니다.
변의 수직이등분선 조건
한 변의 수직이등분선이 아래의 조건을 만족하면 이등변 삼각형입니다.
- 조건: 한 변의 수직이등분선이 대각을 지나면 $\Rightarrow$ 이등변삼각형
[증명]
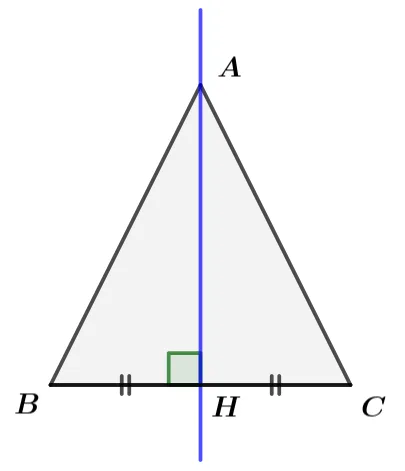
$\triangle{ABC}$에서 $\overline{BC}$의 수직이등분선이 꼭지점$A$를 지나면 $\triangle{ABH}\equiv\triangle{ACH}$ (SAS합동) 입니다.
- $\overline{BH}=\overline{CH}$
- $\angle{AHB}=\angle{AHC}=90^\circ$
- $\overline{AH}$: 공통
따라서 $\overline{AB}=\overline{AC}$이고 이등변삼각형입니다.
정리
위의 증명을 통해 이등변삼각형의 성질과 조건은 다음과 같습니다. (필요충분조건)
- 이등변삼각형의 성질과 조건
- 두 변의 길이가 같다. (정의)
- 두 각의 크기가 같다.
- 꼭지각의 이등분선: 밑변을 수직이등분
- 밑변의 수직이등분선: 꼭지각을 지남
위의 사실을 증명하는 과정에서 다음과 같은 사실을 알 수 있습니다.
- 이등변삼각형에서 다음 선분은 일치한다.
- 꼭지각에서 대변에 그은 중선
- 꼭지각의 이등분선
- 꼭지각의 대변의 수직이등분선
- 꼭지각에서 대변에 내린 수선
수학의 정의
수학에서 어떤 개념A를 설명할 때 개념A의 성질이면서 조건도 되는 것을 정의로 약속합니다.
- 개념A를 B로 정의
- $\text{개념} A \xrightarrow[]{\text{성질}} B$
- $B \xrightarrow[]{\text{조건}} \text{개념} A $
일반적으로 이등변삼각형의 정의를 두 변의 길이가 같은 삼각형으로 약속하여 사용합니다. 하지만, 알아두어야할 것은 다음과 같은 것들도 이등변삼각형의 성질이자 조건이 되므로 정의로 도입할 수 있다는 사실입니다.
- 두 각의 크기가 같다.
- 꼭지각의 이등분선: 밑변을 수직이등분
- 밑변의 수직이등분선: 꼭지각을 지남
