연립방정식의 해의 개수 일차함수로 정리

연립일차방정식을 풀 때, 연립방정식의 해의 개수를 판정할 때, 단순히 계산만으로 접근하는 것보다 직선의 방정식(일차함수)로 이해하면 훨씬 직관적이고 명확합니다.

이 글에서는 연립일차방정식 해를 두 직선의 교점 문제로 바꾸어 해석하고, 기울기와 y절편을 활용해 해의 개수를 그래프로 판정하는 방법을 자세히 살펴봅니다. 또한, 축에 평행한 직선이 포함된 경우의 예외 상황까지 함께 다루어 헷갈릴 수 있는 개념을 명확히 정리했습니다.

개념을 시각적으로 익히고 싶거나, 연립방정식을 그래프와 연결 지어 풀고 싶은 분이라면 이 글이 큰 도움이 될 것입니다. 지금부터 차근차근 함께 살펴보세요!

일차함수와 직선의 방정식(복습)

일차함수 위치관계 판정

두 일차함수 $y=ax+b,\;y’=a’x+b’$의 위치관계를 관계식을 이용해 판정하는 방법은 다음과 같습니다.

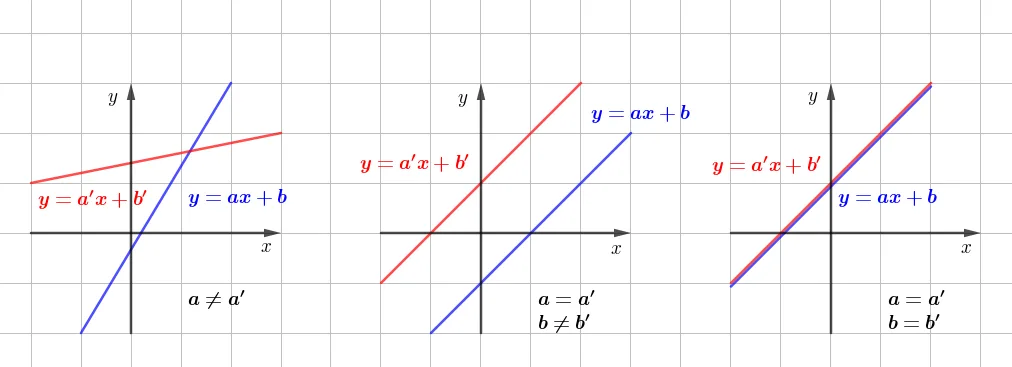
한 점에서 만날 조건: $a \neq a’$ (기울기)
평행한 조건: $a=a’$(기울기), $b\neq b’$ ($y$ 절편)
일치할 조건: $a=a’$(기울기), $b=b’$ ($y$ 절편)

직선의 방정식

$ax+by+c=0$꼴의 일차방정식은 다음과 같이 분류하고 $a,\;b$가 동시에 $0$인 경우는 일차식이 아니므로 이를 제외하면 좌표평면의 모든 직선을 표현할 수 있음을 학습하였습니다.

	$a=0$	$a\neq0$
$b=0$	$0x+0b+c=0$ 일차방정식 아님 ($\bbox[#ffc5fd]{\text{제외}}$)	$ax+0y+c=0$ $x=(\text{상수})$ $y$축과 평행한 직선
$b\neq0$	$0x+by+c=0$ $y=(\text{상수})$ $x$축과 평행한 직선	$ax+by+c=0$ 미지수가 2개인 일차방정식 $y=-\dfrac{a}{b}x-\dfrac{c}{b}$ 일차함수

일차방정식과 직선의 방정식

일차방정식 $ax+by+c=0$은 차수가 1이기 때문에 $a,\;b$가 동시에 $0$이 될 수 없습니다. 따라서 일차방정식 $ax+by+c=0$은 직선의방정식과 같고, 다음과 같이 해석할 수 있음을 학습하였습니다.

직선의 방정식: $\bbox[#ffff00]{\text{일차}}$방정식 $ax+by+c=0$
관계식: $ax+by+c=0$ ($a\neq0$ $\bbox[#ffff00]{\text{또는}}$ $b\neq0$)

연립방정식의 해와 일차함수

다음과 같은 미지수가 2개인 연립일차방정식에 대하여
$\begin{cases} ax+by+c=0\cdotsㄱ\\a’x+b’y+c’=0\cdotsㄴ\end{cases}$
(단, $a\neq0,\;b\neq0,\;a’\neq0,\;b’\neq0$)

$ㄱ,\;ㄴ$은 일차함수로도 생각할 수 있고, 따라서 함수의 그래프를 이용해 연립방정식의 해를 구할 수 있습니다.

연립방정식의 해

연립일차방정식 $\begin{cases} ax+by+c=0\\a’x+b’y+c’=0\end{cases}$의 해는 두 가지 방법으로 생각할 수 있습니다.

가감법, 대입법을 이용한 연립방정식의 해
두 일차함의 교점 좌표 $(\triangle,\;\square)$

예제

연립방정식 $\begin{cases}2x+y=4\cdotsㄱ\\x-y=-1\cdotsㄴ \end{cases}$을 다음 두 가지 방법으로 풀어봅시다.

가감법
일차함수의 그래프

가감법을 이용한 풀이

$\begin{align} &2x+y=4\\
+)&\;x-y=-1\\
\hline
&\quad \;\;3x=3\end{align}$

따라서 연립방정식의 해는 $x=1, \; y=2$입니다.

일차함수의 그래프를 이용한 풀이

$2x+y=4$와 $x-y=-1$의 그래프를 그리는 과정은 다음과 같습니다.

$2x+y=4 \rightarrow {\color{red}y=-2x+4}$
- $x=0$일 때 $y$절편: $4$
- $y=0$일 때 $x$절편: $2$
- $(0,4),\;(2,0)$을 지나는 직선
$x-y=-1\rightarrow {\color{blue}y=x+1}$
- $x=0$일 때 $y$절편: $1$
- $y=0$일 때 $x$절편: $-1$
- $(0,1),\;(-1,0)$을 지나는 직선

위의 사실을 이용해 그래프를 그리면 다음과 같습니다.

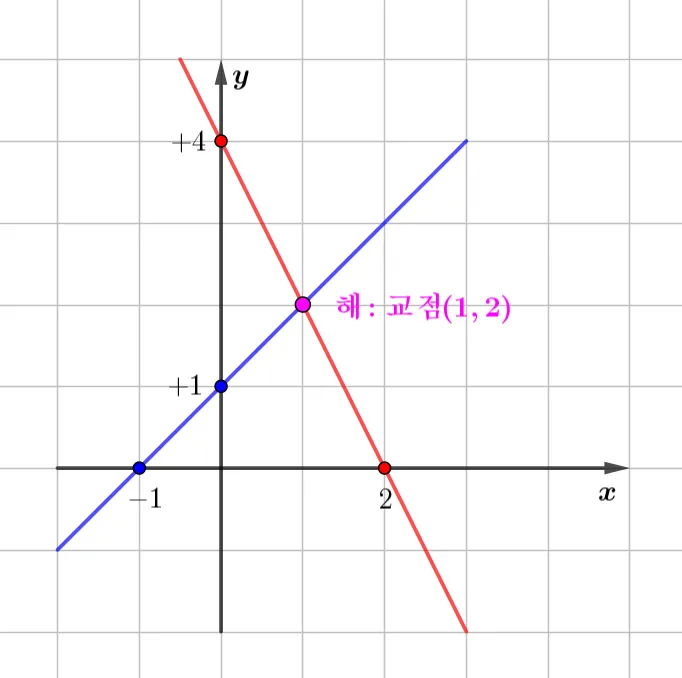
연립방정식의 해는 그래프의 교점을 의미하고 따라서 해는 $(1,2)$입니다.

연립일차방정식의 해의 개수

연립일차방정식$\begin{cases} ax+by+c=0\cdots ㄱ \\a’x+b’y+c’=0\cdotsㄴ \end{cases}$의 각 방정식 ($ㄱ,\;ㄴ$)은 다음과 같이 두 가지로 해석할 수 있습니다.

미지수가 2개인 일차방정식 = 일차함수
미지수가 1개인 방정식 = 축과 평행한 직선

이제 각 경우에 대해 연립일차방정식의 해의 개수를 판정하는 방법에 대해 살펴봅시다.

미지수가 2개인 연립일차방정식
(두 일차함수)

미지수가 2개인 연립일차방정식
$\begin{cases} ax+by+c=0\cdots ㄱ \\a’x+b’y+c’=0\cdotsㄴ \end{cases}$
(단, $a\neq0,\;b\neq0,\;a’\neq0,\;b’\neq0$)의 해의 개수는 다음과 같은 두 가지 방법으로 가능합니다.

일차함수의 기울기, $y$절편 판정
연립방정식을 이용한 판정

일차함수를 이용한 해의 개수 판정

일차함수를 이용한 해의 개수를 판정하는 방법은 다음과 같습니다.
$\begin{cases} y=\bbox[#ffff00]{-\dfrac{a}{b}}x\bbox[#dcff8c]{-\dfrac{c}{b}}\\y=\bbox[#ffff00]{-\dfrac{a’}{b’}}x\bbox[#dcff8c]{-\dfrac{c’}{b’}}\end{cases}$

해가 하나일 조건
- 한 점에서 만난다: $\bbox[#ffff00]{\text{기울기}}$가 다르다.
- $\dfrac{a}{b} \bbox[#ffff00]{\neq}\dfrac{a’}{b’}$(기울기)
해가 없을 조건
- 평행하다: $\bbox[#ffff00]{\text{기울기}}$가 같고, $\bbox[#dcff8c]{y\text{절편}}$이 다르다.
- $\dfrac{a}{b} \bbox[#ffff00]{=} \dfrac{a’}{b’}$(기울기) $\dfrac{c}{b}\bbox[#dcff8c]{\neq} \dfrac{c’}{b’}$ ($y$절편)
해가 무수히 많을 조건
- 일치한다: $\bbox[#ffff00]{\text{기울기}}$가 같고, $\bbox[#dcff8c]{y\text{절편}}$이 같다.
- $\dfrac{a}{b} \bbox[#ffff00]{=} \dfrac{a’}{b’}$(기울기) $\dfrac{c}{b}\bbox[#dcff8c]{=} \dfrac{c’}{b’}$($y$절편)

판정법 변형

비율 변형식을 이용하면 다음과 같이 계수비를 변형할 수 있습니다.

기울기 조건: $\dfrac{a}{b}\bbox[#ffff00]{=}\dfrac{a’}{b’}$ $\Leftrightarrow$ $\dfrac{a}{a’}\bbox[#ffff00]{=}{\color{red}\dfrac{b}{b’}}$
$y$절편 조건: $\dfrac{c}{b}\bbox[#dcff8c]{=}\dfrac{c’}{b’}$ $\Leftrightarrow$ ${\color{red}\dfrac{b}{b’}}\bbox[#dcff8c]{=}\dfrac{c}{c’}$

연립방정식을 이용한 해의 개수 판정

판정법을 적용하면 다음과 같이 식을 변형할 수 있습니다.

해가 하나일 조건: $\dfrac{a}{a’} \bbox[#ffff00]{\neq}{\color{red}\dfrac{b}{b’}}$
해가 없을 조건: $\dfrac{a}{a’} \bbox[#ffff00]{=} {\color{red}\dfrac{b}{b’}}\bbox[#dcff8c]{\neq} \dfrac{c}{c’}$
해가 무수히 많을 조건: $\dfrac{a}{a’} \bbox[#ffff00]{=} {\color{red}\dfrac{b}{b’}} \bbox[#dcff8c]{=} \dfrac{c}{c’}$

미지수가 2개인 연립일차방정식의 해의 개수를 판정하는 방법과 같음을 알 수 있습니다. 연립방정식의 해의 개수를 판정하는 방법에 대해서는 다음 링크를 통해 확인하실 수 있습니다.

연립방정식의 해의 개수 판정

그 밖의 경우
(축과 평행한 직선이 포함)

축과 평행한 직선이 포함된 연립방정식은 다음과 같이 그래프를 이용해 해의 개수를 판단할 수 있습니다.

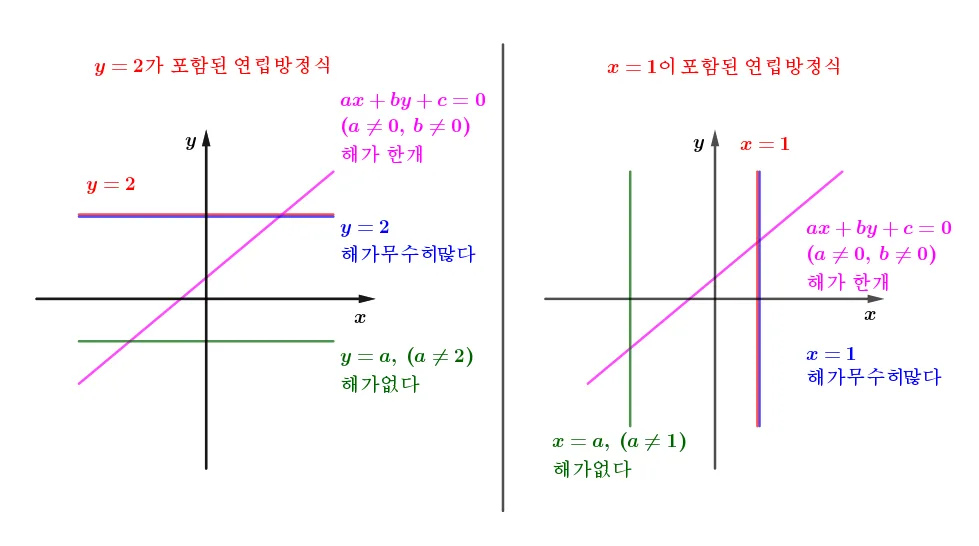
$x$축과 평행한 직선이 포함된 연립일차방정식$\begin{cases} ax+by+c=0\\y=\bbox[#dcff8c]{2}\end{cases}$에서 $ax+by+c=0$의 해의 개수를 $a,\;b$의 조건에 따라 정리하면 다음과 같습니다.

$a\neq0,\;b\neq0$이면 $\color{magenta}\text{일차함수}$꼴이고 해가 한개
$a=0$이면 $y=(\bbox[#ffff00]{\text{상수}})$꼴이고
- $(\bbox[#ffff00]{\text{상수}})\neq\bbox[#dcff8c]{2}$이면 해가 없다.
- $(\bbox[#ffff00]{\text{상수}})=\bbox[#dcff8c]{2}$이면 해가 무수히 많다.
$b=0$이면 $x=(\text{상수})$꼴: 해가 한개

$y$축과 평행한 직선이 포함된 연립일차방정식$\begin{cases} ax+by+c=0\\x=\bbox[#dcff8c]{1}\end{cases}$에서 $ax+by+c=0$의 해의 개수를 $a,\;b$의 조건에 따라 정리하면 다음과 같습니다.

$a\neq0,\;b\neq0$이면 $\color{magenta}\text{일차함수}$꼴이고 해가 한개
$b=0$이면 $x=(\bbox[#ffff00]{\text{상수}})$꼴이고
- $(\bbox[#ffff00]{\text{상수}})\neq\bbox[#dcff8c]{1}$이면 해가 없다.
- $(\bbox[#ffff00]{\text{상수}})=\bbox[#dcff8c]{1}$이면 해가 무수히 많다.
$a=0$이면 $y=(\text{상수})$꼴: 해가 한개

목차