수심의 성질 수족삼각형의 내심과 방심 (원주각 활용)

수심에 대한 내용이 교육과정에 직접 나오지는 않지만, 많은 응용 문제에서 간접적으로 다루고 있습니다. 이번 시간에는 원주각의 성질과 관련된 수심의 성질을 수족삼각형과 수심의 관계를 중심으로 직접 증명하려고 합니다.

중학교 기하에서 출발하지만, 그 과정은 고등학교 모의고사 문제에도 활용될 만큼 의미 있는 결과입니다. 글을 따라가다 보면, 단순히 한 가지 사실을 배우는 것을 넘어 ‘수학적 사고의 확장’을 경험할 수 있을 것입니다.

삼각형의 수심

먼저 삼각형의 수심이 무엇 인지 살펴봅시다.

• 정의 : $\triangle{ABC}$의 각 꼭짓점 에서 대변또는 대변의 연장선에 내린 수선의 교점 (위키백과)

수심의 존재성

수심이 실제로 존재하는지는 다음과 같은 사실을 보이는 것과 같습니다.

• 서로 다른 두 꼭짓점에서 대변(연장선)에 내린 수선의 교점 $H$에 대하여,
  나머지 꼭짓점에서 대변(연장선)에 내린 수선도 $H$를 지난다.

증명

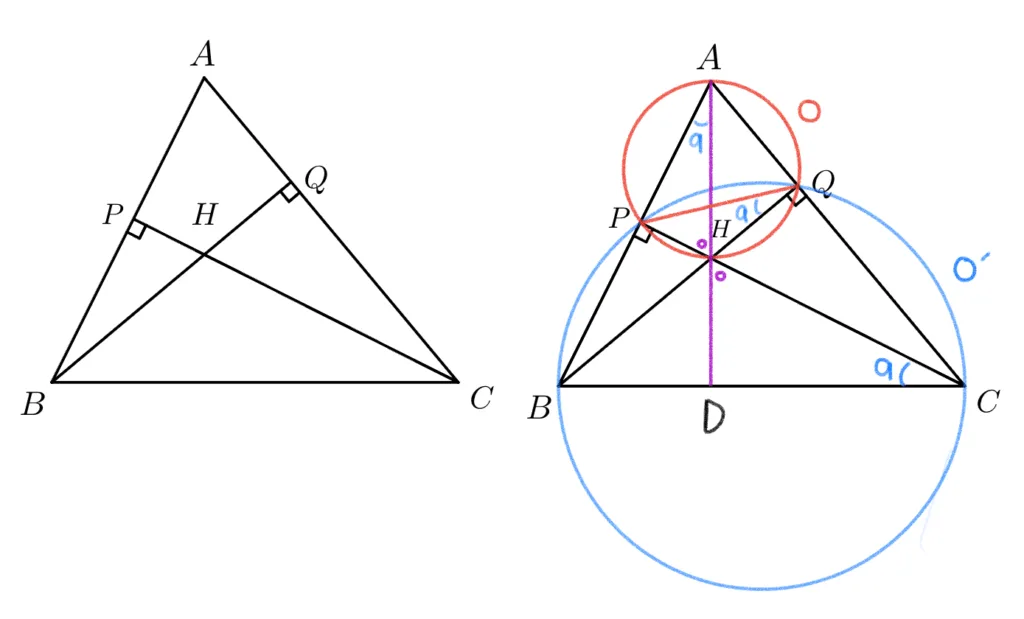
$\square{APHQ},\square{PBCQ}$는 원에 내접하므로 그림과 같이 원을 그리고 원주각의 성질을 적용할 수 있습니다. 이를 이용해 $\triangle{APH}\sm\triangle{CDH}$임을 다음과 같이 보일 수 있습니다.

1. $\angle{PAH}\bbox[#ffff00]{=}\angle{PQH}=\angle{PQB}\bbox[#dcff8d]{=}\angle{PCB}$
   • $\bbox[#ffff00]{\overparen{PH}}$의 원주각
   • $\bbox[#dcff8d]{\overparen{PB}}$의 원주각
2. 맞꼭지각: $\angle{AHP}=\angle{CHD}$

따라서 $\angle{APH}=\angle{CDH}=90^\circ$이고 $\overline{AD}\perp \overline{BC}$가 성립합니다.

수심의 성질과 수족삼각형

$\triangle{ABC}$의 꼭짓점 $A,B,C$에서 대변(연장선)에 내린 수선의 발 $P,\ Q,\ R$을 꼭짓 점으로 하는 $\triangle{PQR}$을 수족삼각형 이라고 하고 다음과 같은 성질이 있습니다.

증명: 예각삼각형의 수심은 수족삼각형의 내심이다.

$\square{APQH},\square{PBCQ}$와 $\square{ABDQ},\square{QHDC}$가 원에 내접하는 사각형임을 이용하면 $\overline{QH}$가 $\angle{PQR}$을 이등분함을 아래와 같이 보일 수 있습니다.

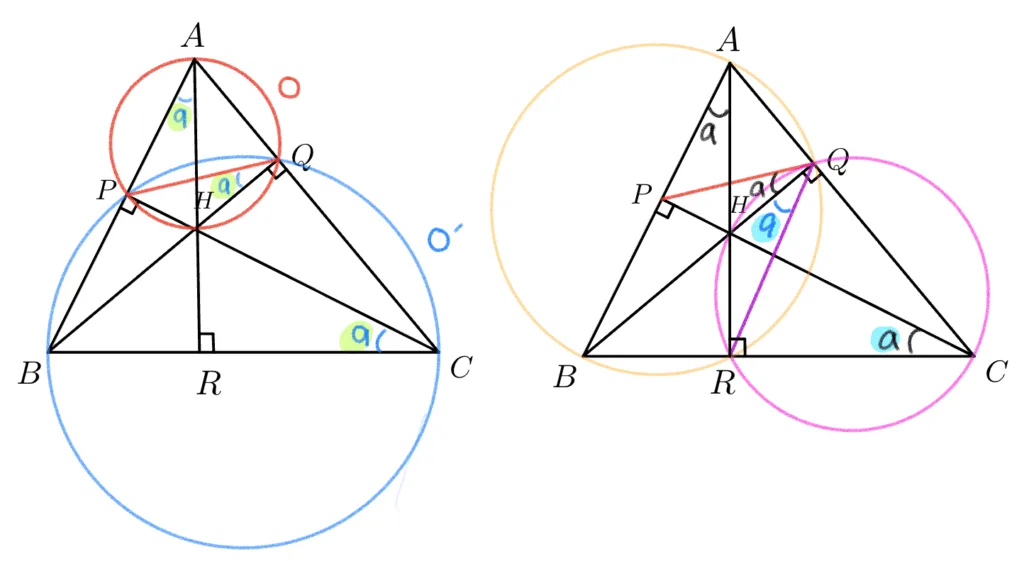
이를 종합하면 $\overline{QH}$는 $\angle{PQD}$의 각의 이등분선이 됩니다. 비슷한 방법으로 $\overline{PH},\ \overline{RH}$는 $\triangle{PQR}$에서 각의 이등분선이 되고, $H$는 내심이 됨을 알 수 있습니다.

증명: 둔각삼각형의 수심은 수족삼각형의 방심이다.

$\square{APCR}, \square{QPBH}, \square{ABRQ}, \square{QCRH}$는 원에 내접하는 사각형입니다.

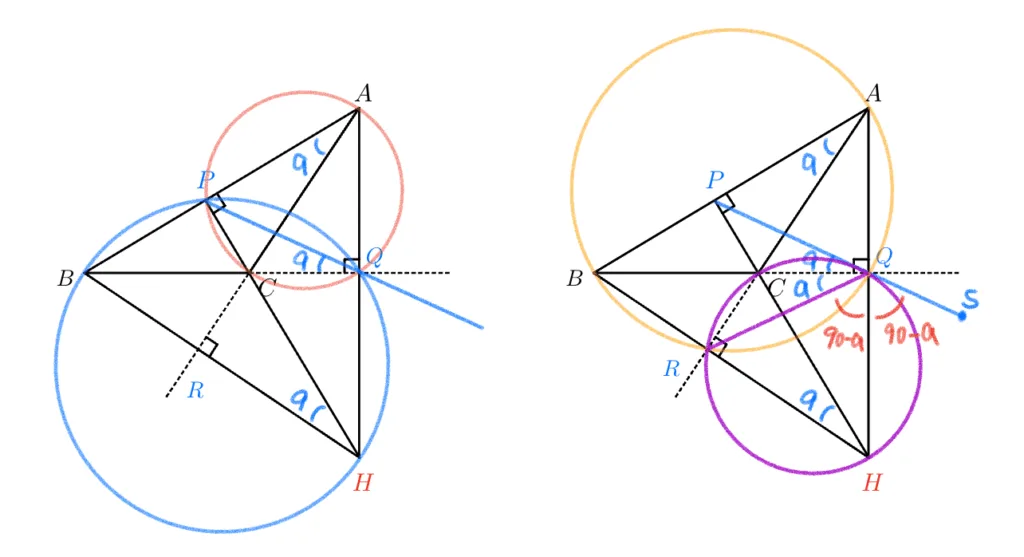
다음과 같은 이유로 $\overline{QH}$는 $\angle{RQS}$의 이등분선입니다.

• $\angle{CQH}=90^{\circ}$ 이므로 $\angle{RQH}=90^{\circ}-a$이다.
• $\angle{RQS}=180-2a$ 이므로 $\angle{HQS}=\angle{RQH}=90^{\circ}-a$이다.

이를 종합하면 $H$는 $\triangle{ABC}$의 한 내각의 이등분선과 두 외각의 이등분선의 교점입니다. 따라서 $H$는 $\triangle{ABC}$의 방심이 됩니다.

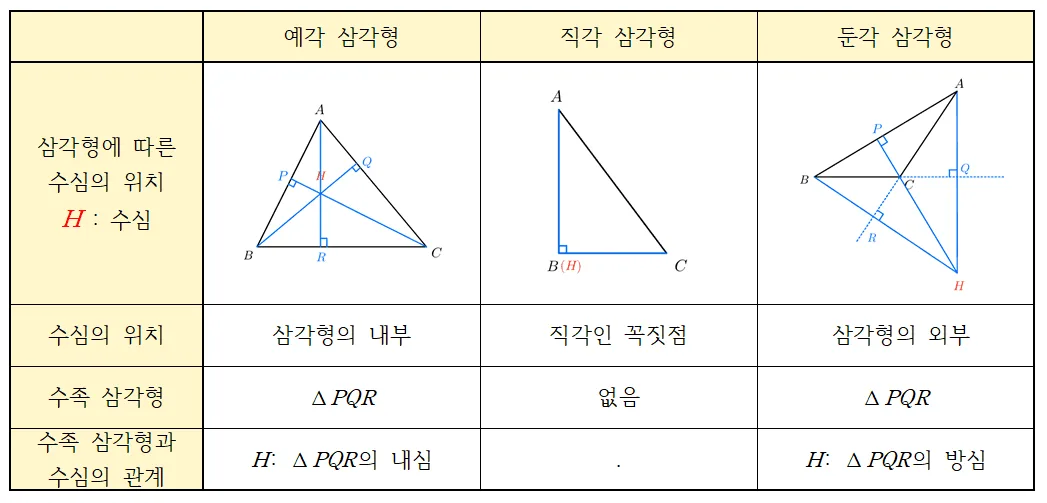
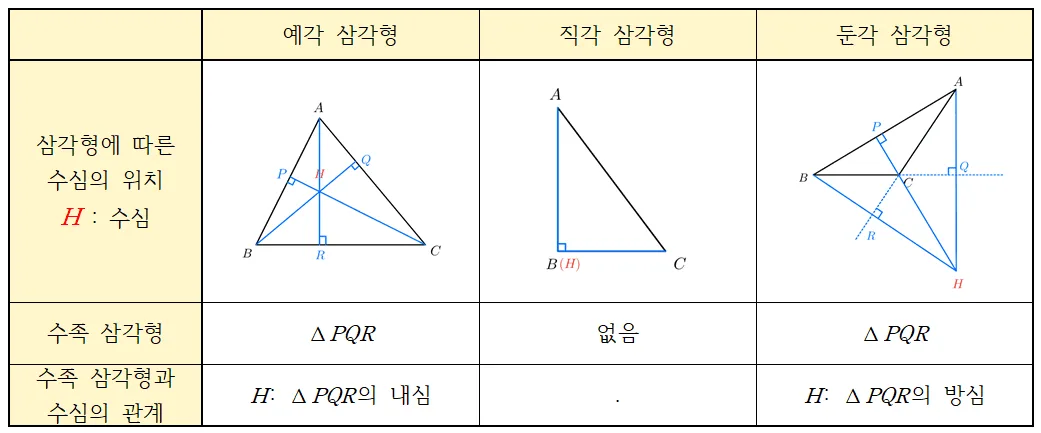
수심의 위치와 성질 정리

위의 내용을 다시 한번 정리하면 다음과 같습니다.