삼각형 무게중심 성질은 중학교 도형 단원에서 가장 중요한 개념 중 하나입니다. 무게중심은 세 중선이 한 점에서 만난다는 사실과 그 점이 각 꼭짓점으로부터 $2:1$의 비로 중선을 나눈다는 성질이 있습니다. 이번 글에서는 삼각형의 중선의 정의와 성질을 정리하고, 무게중심의 존재성과 성질을 증명하는 과정을 단계별로 살펴보겠습니다.
삼각형의 중선
먼저 삼각형의 중선과 그 성질에 대해 정리해 봅시다.
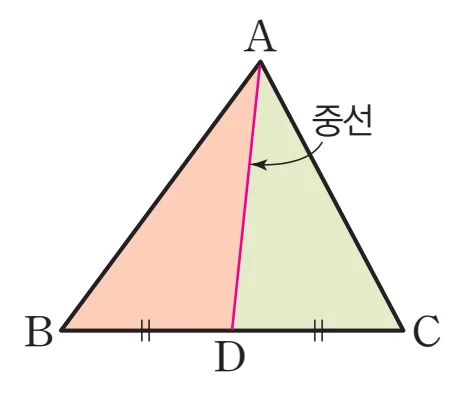
- 삼각형의 중선: 삼각형의 한 꼭짓점과 그 대변의 중점을 이은 선분
- 한 삼각형에는 세 개의 중선이 있음.
- 삼각형의 중선의 성질
- 삼각형의 중선은 그 삼각형의 넓이를 이등분한다.
$\triangle ABC$에서 $\overline{AD}$가 중선이면 $\triangle ABD = \triangle ADC = \dfrac{1}{2}\triangle ABC$
- 삼각형의 중선은 그 삼각형의 넓이를 이등분한다.
중선에 대해 정리할 기회가 없기 때문에 3학년 1학기 곱셈공식과 피타고라스 정리를이용해 파푸스 중선정리를 정리하고 넘어가도록 하겠습니다.
파푸스 중선정리 (중3)
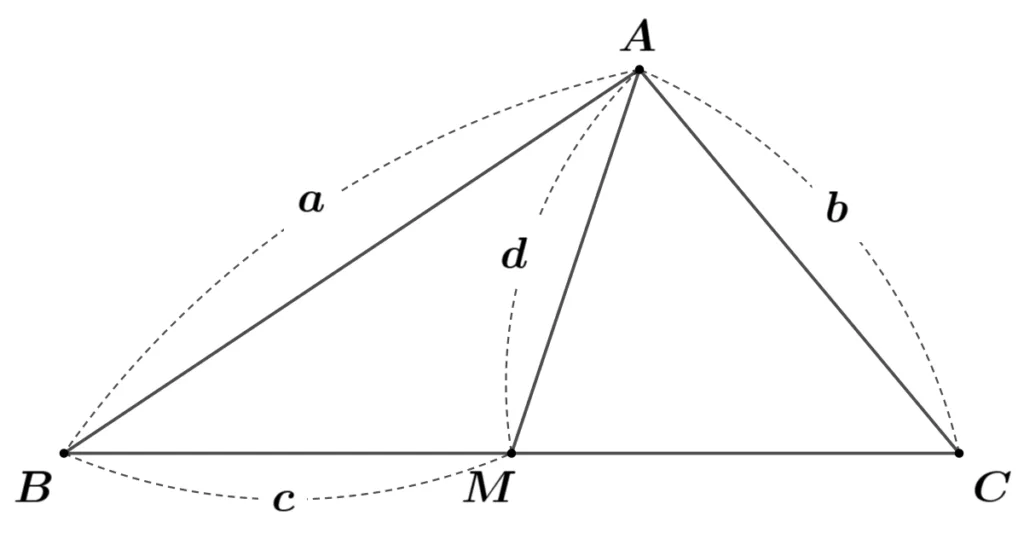
$\triangle ABC$의 한 점 $A$에서 대변에 그은 중선 $\overline{AM}$에 대하여
$\overline{AB}=a$, $\overline{AC}=b$, $\overline{BM}=c$, $\overline{AM}=d$ 일 때 다음이 성립합니다.
- $a^2+b^2=2(c^2+d^2)$
증명
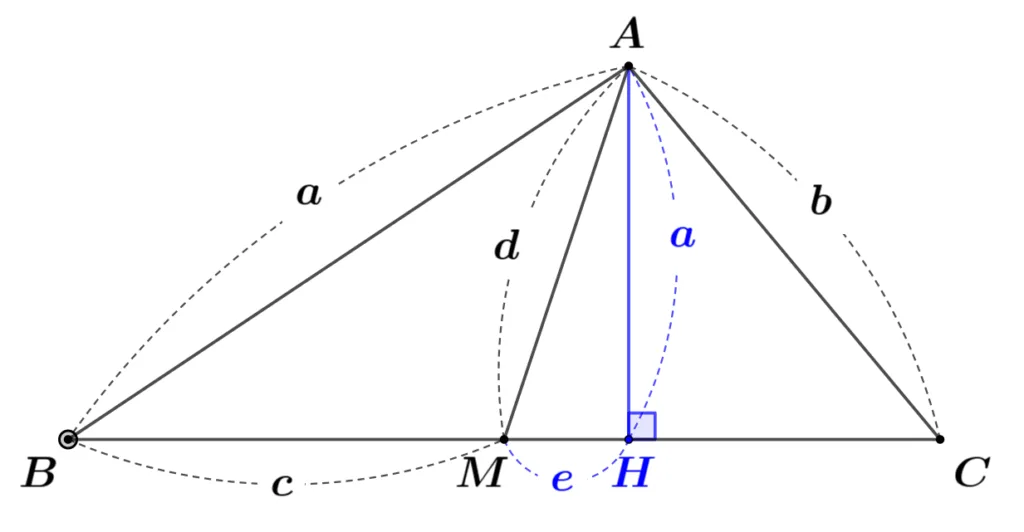
$\triangle ABC$의 한 점 $A$에서 대변에 내린 수선의 발이 $H$일 때 $\overline{AH}=h$, $\overline{MH}=e$라고 하면,
피타고라스 정리에 의해 다음이 성립합니다.
\begin{flalign} {\color{blue}a^2}+{\color{red}b^2}&={\color{blue}(c+e)^2+h^2}+{\color{red}(c-e)^2+h^2}\\
&=2(c^2+\bbox[#ffff00]{e^2+h^2})\\
&=2(c^2+\bbox[#ffff00]{d^2}) &&\end{flalign}
삼각형 무게중심
- 삼각형의 무게중심: 삼각형의 세 중선의 교점
- 삼각형의 무게중심의 성질
- 삼각형의 세 중선은 한 점(무게중심)에서 만난다.
- 삼각형의 무게중심은 세 중선의 길이를 각 꼭짓점으로부터 $2:1$로 나눈다.
$\triangle ABC$에서 점 $G$가 무게중심이면
$\overline{AG}:\overline{GD} = \overline{BG}:\overline{GE} = \overline{CG}:\overline{GF} = 2:1$
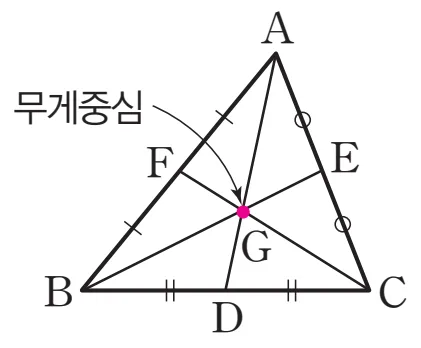
무제중심에 대해 생각하려면 세 중선의 교점이 한 점에서 만나는지 확인부터 해야 합니다. 따라서 세 중선이 한 점에서 만나는 점이 존재함을 보이는 아래와 같은 과정이 필요합니다.
증명 (존재성)
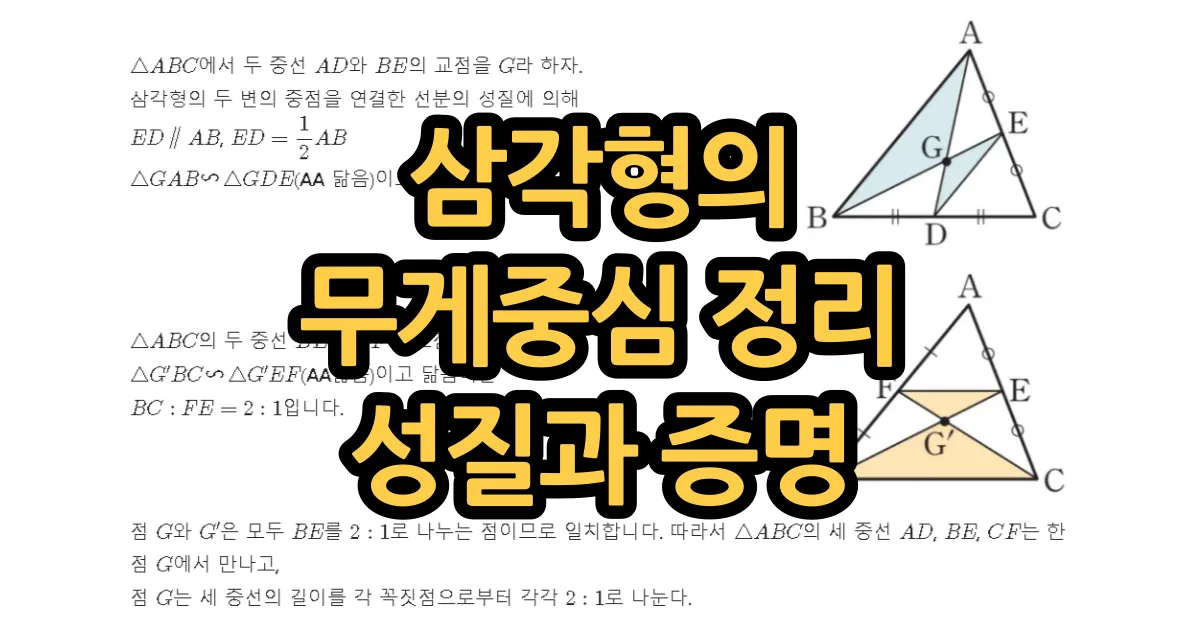
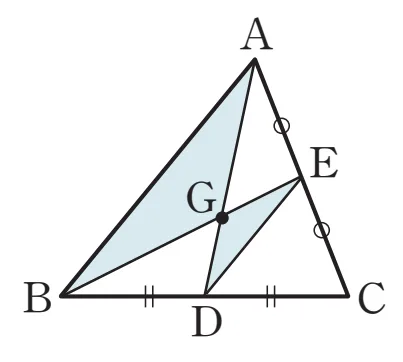
$\triangle ABC$에서 두 중선 $\overline{AD}$와 $\overline{BE}$의 교점을 $G$라 하자.
중점연결정리에 의해
$\overline{ED} \pa \overline{AB}$, $\overline{ED} = \dfrac{1}{2}\overline{AB}$
$\triangle GAB \sm \triangle GDE$(AA 닮음)이고 닮음비는 $\overline{AB} : \overline{ED} = 2:1$입니다.
$\triangle ABC$의 두 중선 $\overline{BE}$와 $\overline{CF}$의 교점을 $G’$라 하면, $\triangle G’BC \sm \triangle G’EF$(AA닮음)이고 닮음비는
$\overline{BC} : \overline{FE} = 2:1$입니다.
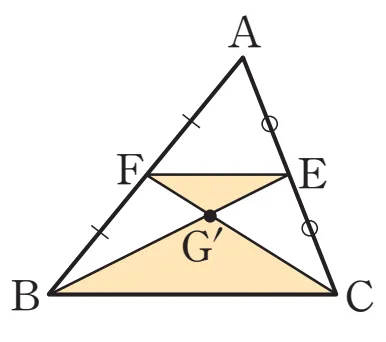
점 $G$와 $G’$은 모두 $\overline{BE}$를 $2:1$로 나누는 점이므로 일치합니다. 따라서 $\triangle ABC$의 세 중선 $\overline{AD}$, $\overline{BE}$, $\overline{CF}$는 한 점 $G$에서 만나고,
점 $G$는 세 중선의 길이를 각 꼭짓점으로부터 각각 $2:1$로 나눈다.
참고
- 이등변삼각형의 무게중심은 꼭지각의 이등분선(밑변의 수직이등분선) 위에 있다.
- 꼭지각에서 중선은 각의 이등분선, 밑변의 수직이등분선이다.
- 정삼각형의 외심, 내심, 무게중심은 모두 일치한다.
- 정삼각형은 이등변삼각형이므로 세 각의 이등분선 (내심)은 대변의 수직이등분선(외심)이고 중선(무게중심)이다.
출처: 개념원리