삼각형 안에는 꼭짓점, 무게중심, 외심, 내심처럼 수많은 특별한 점들이 숨어 있습니다. 그중에서도 방심은 흔히 지나치기 쉬우나, 중학교 기하의 여러 단원과 깊게 연결되는 중요한 개념입니다.
삼각형의 방심은 단순히 정의만 외우는 것이 아니라, 각의 이등분선의 성질, 접선의 길이 공식, 합동 조건, 직각삼각형의 성질 등 앞으로 배우게 될 기하 단원들과 자연스럽게 이어집니다. 방심의 존재와 성질을 이해하면, 이후 닮음 증명, 삼각형 둘레 공식, 삼각비 활용까지 학습할 때 논리적 연결고리를 더 쉽게 찾을 수 있습니다.
이 글에서는 방심과 방접원의 정의에서 출발해, 그 존재성의 증명, 접선의 길이 응용, 그리고 직각삼각형에서의 방심 활용까지 차근차근 살펴보겠습니다. 방심에 대한 내용을 정리하면서, 중학교 기하에 대한 통찰을 얻길 바랍니다.
방접원과 방심
삼각형의 방접원과 방심은 다음과 같이 정의합니다.
- 방접원: 주어진 삼각형의 한 변에 접하고 남은 두 변의 연장선에 접하는 원
- 방심: 방접원의 중심
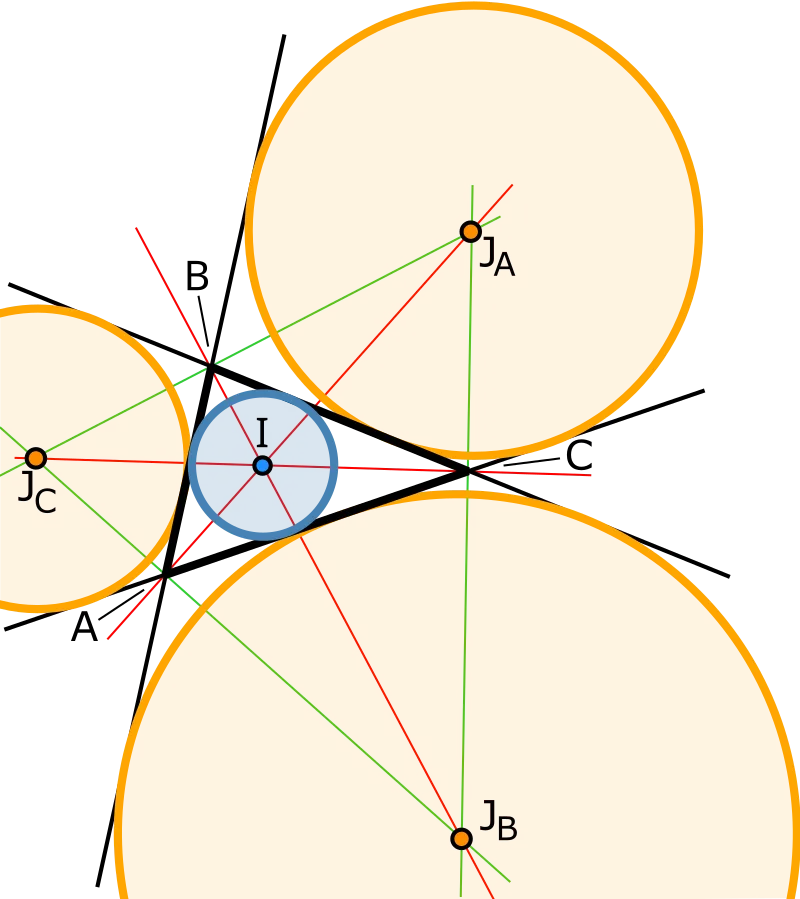
그림과 같이, 삼각형에는 세 변을 따라 3개의 방접원과 3개의 방심이 있습니다.
방심의 성질
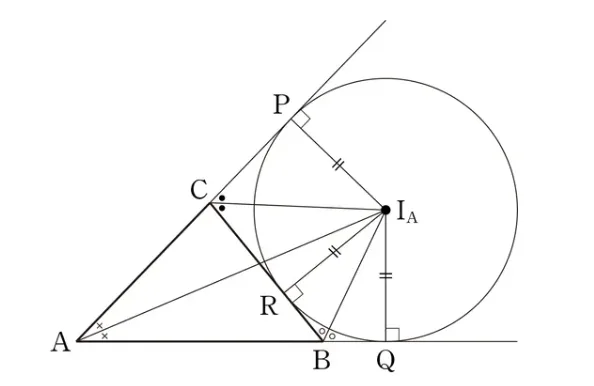
삼각형의 한 변에 접하고 남은 두 변의 연장선에 접하는 방접원의 중심 $O$에 대하여 다음이 성립합니다.
- $\overline{IP}=\overline{IQ}=\overline{IR}$
따라서 $I$는 각의 이등분선 위에 있고, 다음이 성립합니다. (각의 이등분선 위의 점의 성질과 조건)
- $\overline{CI}$: $\angle{PCR}$의 이등분선
- $\overline{BI}$: $\angle{RBQ}$의 이등분선
- $\overline{AI}$: $\angle{CAB}$의 이등분선
방심의 존재성
삼각형의 한 변에 접하고 남은 두 변의 연장선에 접하는 원이 존재하는지 확인하는 과정은 다음의 성질을 만족하는 점이 존재함을 보이는 것과 같습니다.
- 한 내각의 이등분선은 서로 다른 두 외각의 이등분선의 교점을 지나고 이 점이 방심이 된다.
[증명]
주어진 $\triangle{ABC}$에서 $\angle{C},\ \angle{B}$의 외각의 이등분선이 만나는 점 $I$에 대하여 다음이 성립합니다.
- $I$ 각의 이등분선 위의 점: $\overline{IP}=\overline{IR}=\overline{IQ}$
반지름이 $\overline{IP}=\overline{IR}=\overline{IQ}=R$인 원을 그리면 방접원이 됨을 알 수 있습니다. 추가적으로 다음과 같은 사실도 알 수 있습니다.
- 한 내각의 이등분선이 다른 두 외각의 이등분선의 교점$I$를 지난다.
$\triangle{IAP} \equiv \triangle{IAQ}$ (RHS합동)
방심의 응용
접선의 길이 응용
$\triangle{ABC}$의 두 외각의 이등분선의 교점 $O$에 대하여 다음이 성립합니다.
- ($\triangle{ABC}$의 둘레)$=2\overline{BE}=2\overline{BD}$
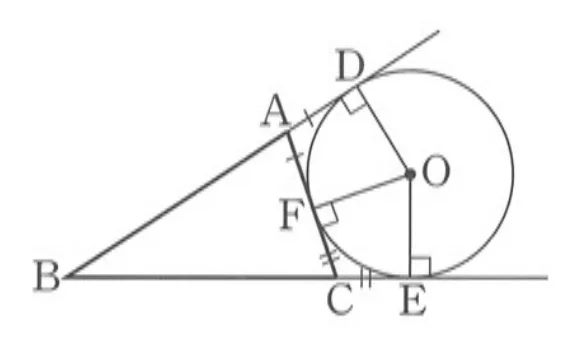
[증명]
$\triangle{ABC}$의 두 외각의 이등분선의 교점 $O$는 방접원의 중심이고 방접원과 접점을 $D,\ E,\ F$라고 할 때 다음을 만족합니다.
- 접선의 길이: $\overline{AF}=\overline{AD}$, $\overline{CF}=\overline{CE}$
\begin{flalign} (\triangle{ABC}&\text{의 둘레})\\
&= \overline{AB}+\overline{BC}+\bbox[#ffff00]{\overline{CA}}\\
&=\overline{AB}+\overline{BC}+\bbox[#ffff00]{\overline{AF}+\overline{CF}}\\
&=\overline{BD}+\overline{BE}\\
&=2\overline{BE}\ (\because \overline{BD}=\overline{BE})&&\end{flalign}
직각삼각형의 방심
직각삼각형 $\triangle{ABC}$의 두 외각의 이등분선의 교점 $O$에 대하여 방접원의 반지름 $r$은 다음을 만족합니다.
- $r=\overline{BD}-\overline{BC}$
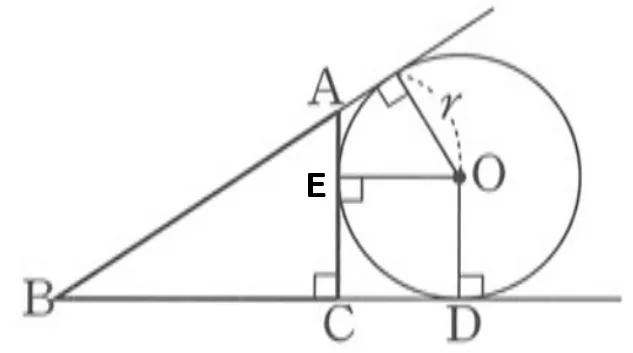
[증명]
방심 $O$에서 내린 수선의 발 $E,\ D$에 대하여 $\angle{ECD}=90^\circ$이므로 $\square{CDOE}$의 네 각의 크기가 $90^\circ$이고 직사각형임을 알 수 있습니다.
직사각형 $\square{CDOE}$의 이웃하는 변 $\overline{OE}=\overline{OD}$이므로 $\square{CDOE}$는 정사각형이 됩니다. 따라서 방접원의 반지름의 길이가 $r=\overline{CD}=\overline{BD}-\overline{BC}$임을 알 수 있습니다.
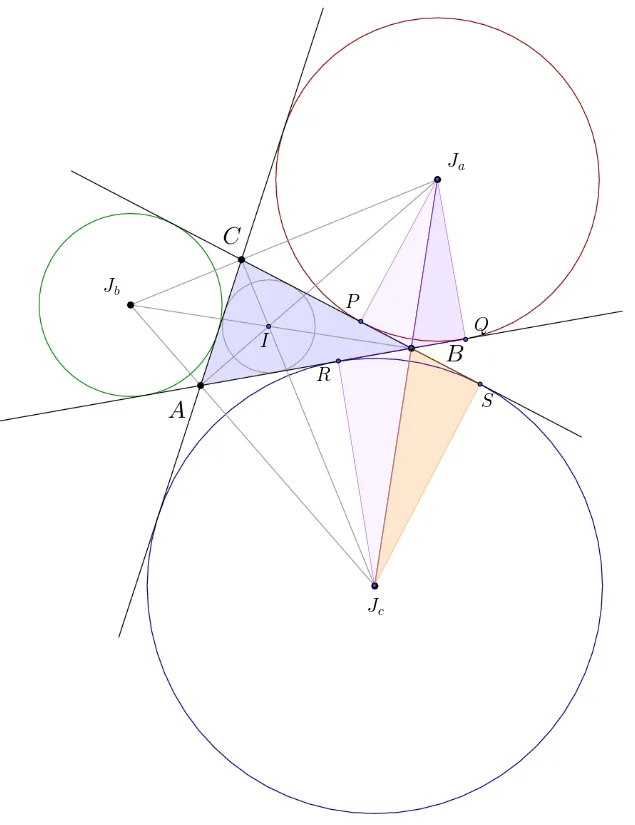
[이미지 출처: 위키피디아, 에이급수학]