함수의 정의 용어와 기호

수학에서 ‘함수’는 단순한 계산식이 아니라, 변수 사이의 관계를 이해하는 데 꼭 필요한 개념입니다. 중학교 1학년 때 배운 ‘정비례’를 바탕으로, 변수들이 어떤 방식으로 연결되어 있는지를 함수라는 개념으로 확장해봅시다. 이 글에서는 먼저 정비례 개념을 간단히 복습한 뒤, 함수의 정의와 기본 용어, 그리고 이를 수학적으로 어떻게 기호로 나타내는지를 단계적으로 정리하고, 함수가 왜 중요한지, 어떤 조건에서 함수라고 할 수 있는지 예시를 통해 쉽고 명확하게 설명하였습니다.

복습 : 정비례

함수에 대해 정리하기 전 중학교 1학년에서 배운 정비례에 대해 정리해 봅시다.

두 변수 사이의 비($x:y$)가 일정하면 $x$에 대한 $y$의 비율은 다음과 같고 이 때 $x,\;y$가 정비례 관계에 있다고 합니다.

• $x:y=\text{일정}\rightarrow$$\dfrac{y}{x}=a (\text{상수}), \; a\neq 0$
• $y=ax\;(a\neq0)$

함수 정의 용어 기호

함수는 $\bbox[#ffff00]{\text{입력값(독립변수)}}$을 하나를 받아 $\bbox[#dcff8c]{\text{출력값(종속 변수)}}$을 $\bbox[#94feff]{\text{오직 하나}}$만 반환하는 상황을 수학적으로 나타내는 방법입니다.

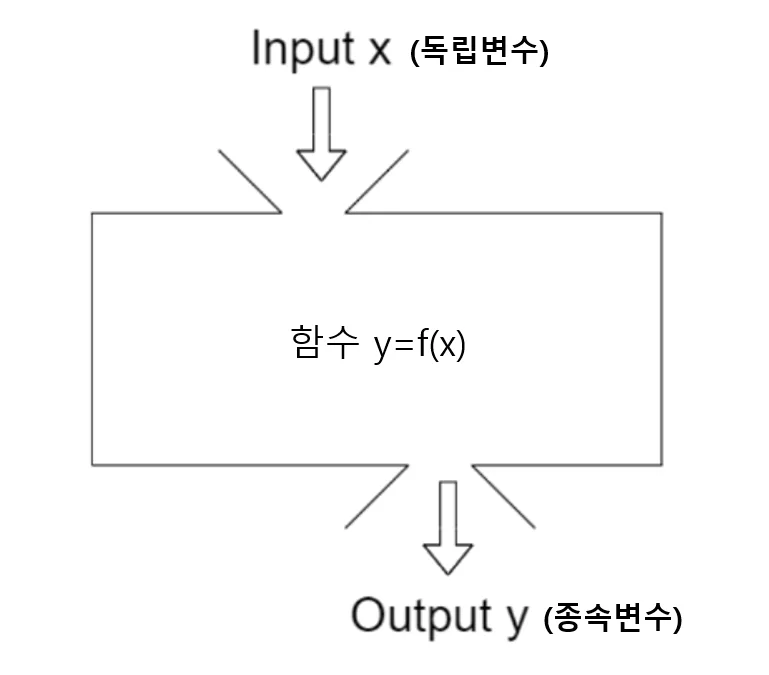
함수의 정의

두 변수 $x,\; y$에 대하여 함수의 정의와 용어에 대해 정리하면 다음과 같습니다.

• 정의: $x$값 하나$\rightarrow$ $y$값이 오직 하나씩 결정되면 $y$는 $x$의 함수 라고 합니다.

$x$값 하나에 $y$값이 2개 이상 정해지면 함수가 아닙니다.

함수는 영어로 function이고 첫 글자 $f$를 기호화 하여 사용합니다. 서로 다른 함수를 나타낼 때 $f,\;g,\;h$를 순서대로 사용하는 것이 관례입니다.

용어와 기호

1. 기호: ‘$y$는 $x$의 함수’를 $f$라고 할 때 기호는 다음과 같습니다.
   • $x\xrightarrow[]{\quad f \quad} y$ 
   • $y=\bbox[#ffff00]{f}(x)$
2. $f$와 다른 $\bbox[#dcff8c]{\text{함수}(g)}$: $y=\bbox[#dcff8c]{g}(x)$로 구분

$f(x)$는 함수 $f$에 대한 함숫값을 의미하고 다음과 같이 사용합니다.

1. $\bbox[#ffff00]{f}(\bbox[#94feff]{\square})$: 함수 $\bbox[#ffff00]{f}$의 $\bbox[#94feff]{\square}$에 대한 함숫값
2. $f(a)$의 의미
   • 함수 $\bbox[#ffff00]{f}$의 $x=a$에서 함숫값
   • 함수 $\bbox[#ffff00]{f}$의 $x=a$에서 $y$값
   • $\bbox[#ffff00]{f}(x)$에 $x=a$를 대입한 값
3. $f(x)$: 함수 $\bbox[#ffff00]{f}$에서 $x$에 대한 함숫값

용어 적용

$y=3x$에 대한 대응표는 다음과 같고 $x$값 하나에 $y$값이 하나만 결정되므로 함수라고 할 수 있습니다.

$x$	-2	-1	0	1	2
$y = 3x$	-6	-3	0	3	6

$y$= (자연수 $x$의 약수)에 대한 대응표는 다음과 같고 $x$값 하나에 여러개 $y$값을 가지는 경우가 있으므로 함수가 아닙니다.

$x$	1	2	3	4	5
$y=$($x$약수)	1	1,2	1,3	1,2,4	1,5

두 함수 $y=3x,\;y=2x-1$에 대하여 위의 용어를 적용해 봅시다.

1. $y=3x$를 함수 $f$로 두면 $y=2x-1$는 함수 $g$로 둘 수 있습니다.
2. $y=3x$를 $f$로 표현: $y=f(x)$이고 $f(x)=3x$
3. $y=2x-1$를 $g$로 표현: $y=g(x)$이고 $g(x)=2x-1$
4. $f(2)=3\times2$이고 $g(-3)=2\times(-3)-1=-7$입니다.

위의 예시에서 $y=3x,\;y=2x-1$로 표현된 식을 각각함수의 관계식이라고 합니다.

• $y=3x$: 함수 $f$의 관계식
• $y=2x-1$:함수 $g$의 관계식

함수의 그래프

$y=f(x)$에서 $x$ 값과 그 값에 따라 하나로 정해지는 함숫값 $y$의 순서쌍 $(x,y)$를 점으로 좌표평면에 나타낸 것을 함수의 그래프라고 합니다.

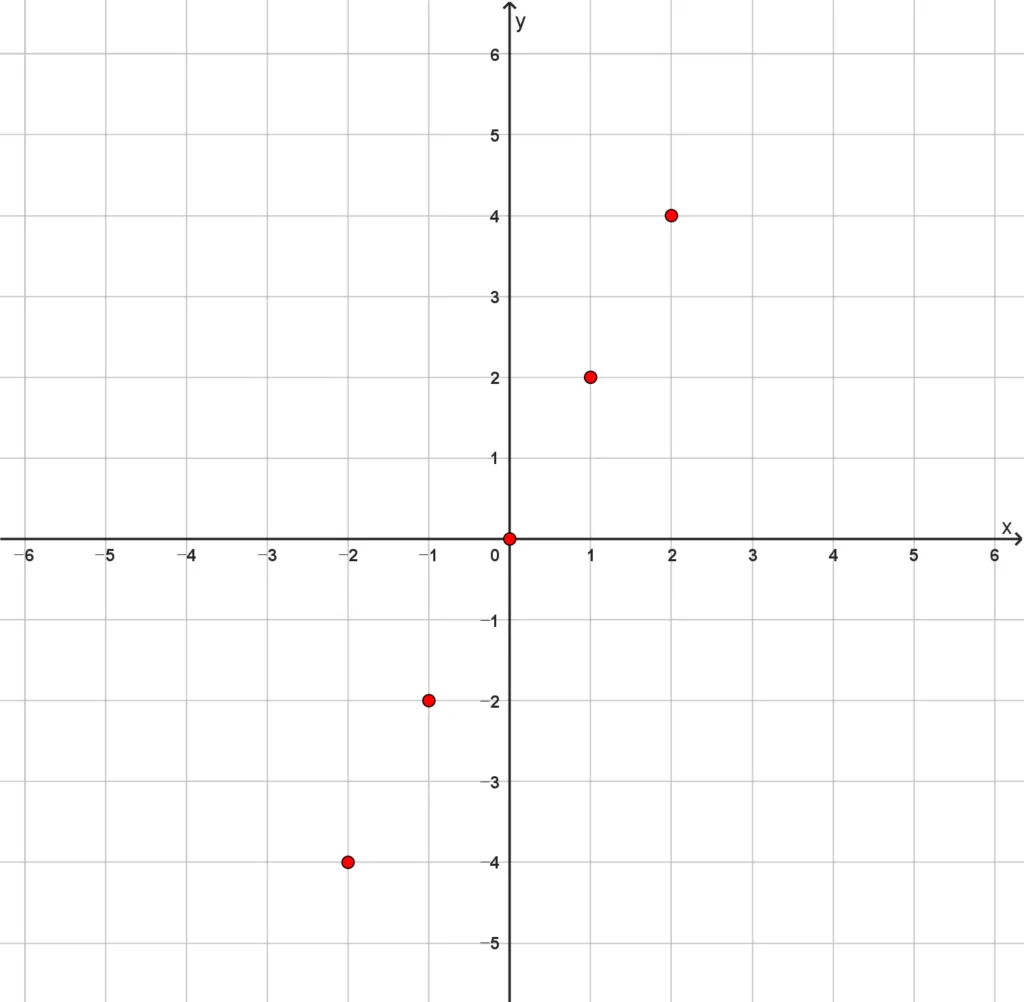
위에서 예로 들었던 $y=2x$의 대응표는 다음과 같습니다.

$x$	-2	-1	0	1	2
$y = 2x$	-4	-2	0	2	4

대응표를 순서쌍으로 나타내면 $\cdots(-2,-4),\;(-1,-2),\;(0,0),\;(1,2),\;(2,4)\cdots$이고 이를 좌표 평면에 나타내는 과정은 다음과 같습니다.

1. $\cdots(-2,-4),\;(-1,-2),\;(0,0),\;(1,2),\;(2,4)\cdots$을 좌표평면에 나타낸다.
2. $x$값이 유리수인 경우로 확장하여 좌표평면에 나타낸다.

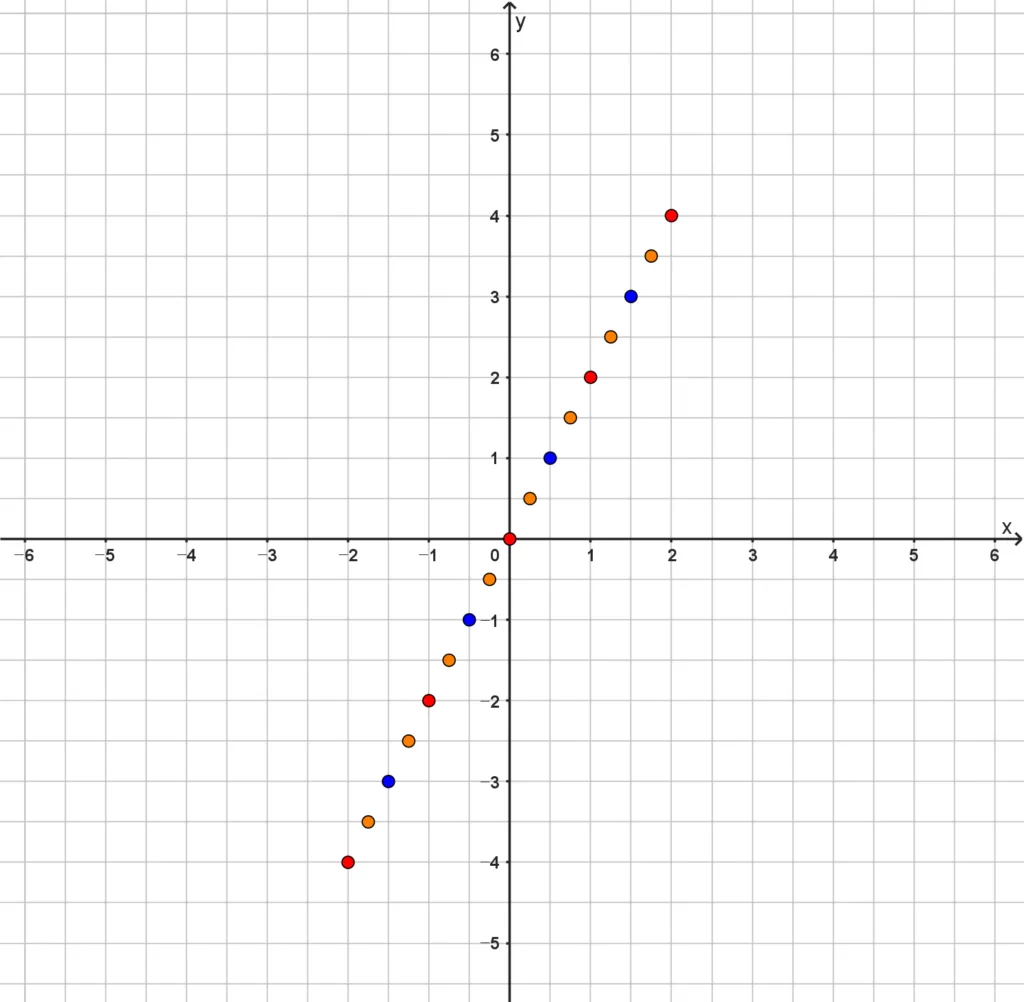
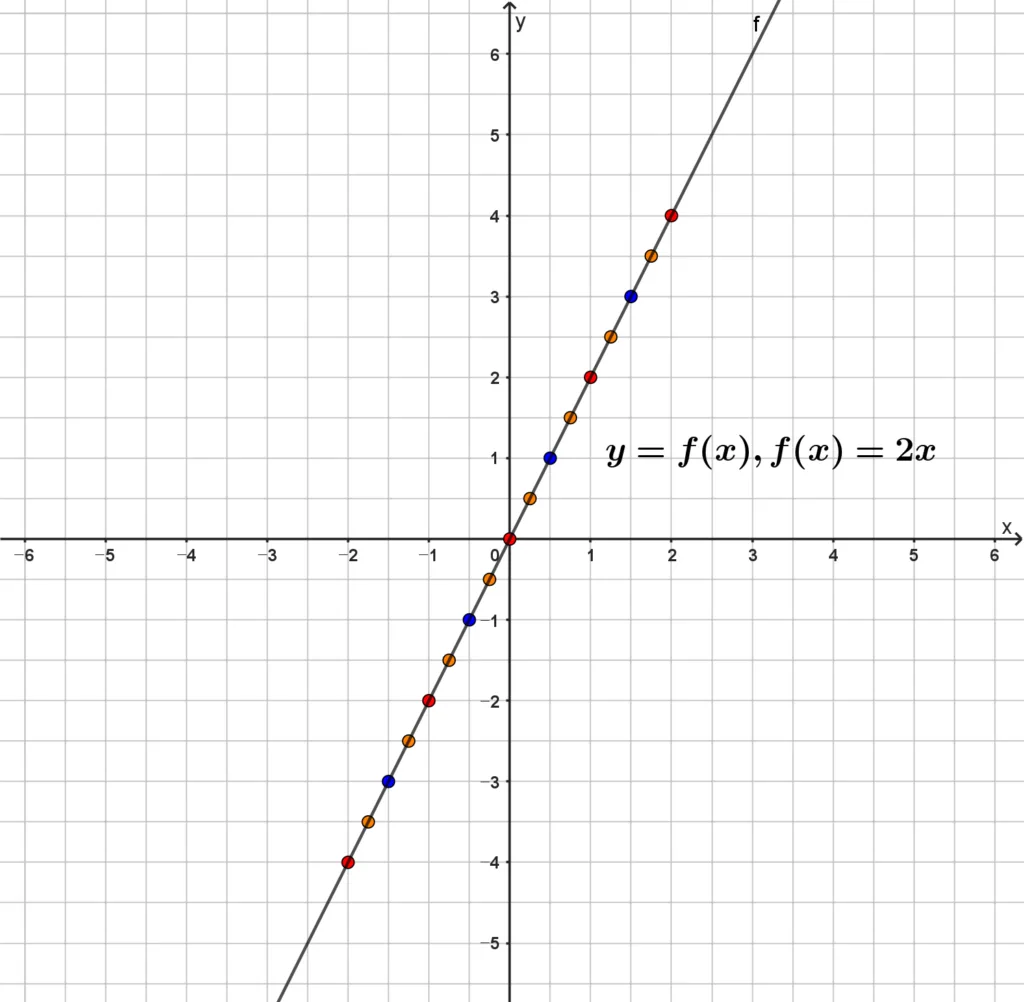
중학교 1학년에 학습한 정비례 관계와 그래프는 함수로 다음과 같이 나타낼 수 있고 각 기호의 의미는 다음과 같습니다.

• $y=f(x),\; f(x)=2x$
  1. $y=f(x)$: $y$는 $x$의 함수 $f$
  2. $f(x)=2x$: 함수 $f$의 관계식이 $2x$

다음 시간에는 중학교 1학년때 배운 정비례를 함수 개념으로 확장하여 일차함수에 대해 배워 보도록 하겠습니다.

중학교에서 배운 함수 개념은 고등학교, 대학교 까지 확장되는 개념으로 각 단계별 정의는 아래의 나무 위키를 통해 확인하실 수 있습니다.

• 함수의 정의 나무위키