이번 시간에는 예시를 통해 정비례의 정의를 학습하고 이를 토대로 성질, 일반형 관계식, 그래프, 그래프의 성질을 정리해 보려고 한다. 공식처럼 외우면 간단한 내용일 수 있지만 체계적으로 정리하며 학습하는 것이 수학에 대한 흥미를 잃지 않는 방법이다. 이번 기회에 정비례를 체계적으로 정리해 보길 바랍니다.
목차
정비례 예시
정비례 관계에 대해 수학적으로 정리하기 전에 먼저 다음 예시를 통해 두 변수($x,\;y$) 사이의 관계에 대해 살펴보자.
- 사탕 $1$개의 가격이 $300$원이라고 할 때
사탕 $x$ 개를 구매하고 지불해야 하는 금액 $y$ 사이의 관계.
$\begin{align} x=&\;\;1\quad \quad 2\;\;\;\quad 3\quad \; \quad 4\quad \quad\;\; 5 \quad \cdots\\[1em]
y=\;&300\quad 600\quad 900\quad 1200\quad 1500\; \cdots \\[1em]\end{align}$
사탕의 개수($x$)와 지불할 금액($y$) 사이의 관계를 정리하면 다음과 같은 결과를 얻을 수 있다.
$x\;:\;y=1:300=2:600=3:900\;\cdots\\[1em]$
$\begin{cases}1:300\xrightarrow[\;y:\;2\text{배}\;]{\;x:\;2\text{배}\;}2:\;\;600\\[1em]
1:300\xrightarrow[\;y:\;3\text{배}\;]{\;x:\;3\text{배}\;}3:\;\;900\\[1em]
\quad \cdots \end{cases}$
위의 결과를 통해 두 변수 사이의 관계는 다음을 만족하고 함수임을 알 수 있다.
- $x$값이 $2$배, $3$배, $4$배 $\cdots$ 이면
$y$값도 $2$배, $3$배, $4$배 $\cdots$ 가 되는 관계
이러한 조건을 만족하는 관계를 정비례 관계라고 한다. 이제 정비례의 정의와 성질에 대해 정리해 보기로 하자.
정비례의 정의와 성질
정비례의 정의
두 변수 $x$, $y$에 대하여 다음과 같은 성질을 만족하는 관계를 ‘정비례’라고 한다.
- $x$값이 $2$배, $3$배, $4$배, $\cdots $ 됨에 따라
$y$값도 $2$배, $3$배, $4$배 $\cdots$ 가 되는 $\bbox[#ffff00]{\text{함수}}$관계
정비례 관계는 $x$값에 따라 $y$값이 오직 하나로 결정되기 때문에 $\bbox[#ffff00]{\text{함수}}$이다.
정비례의 성질
$\bbox[#ffff00]{x\text{값}}$이 $2$배, $3$배, $4$배 $\cdots\ \bbox[#ffc5fd]{\square}$배 됨에 따라 $\bbox[#dcff8c]{y\text{값}}$도 $2$배, $3$배, $4$배$\cdots\ \bbox[#ffc5fd]{\square}$배 가 될 때 다음과 같은 이유로 비율이 항상 일정하다.
$\bbox[#ffff00]{x\text{값}}$과 $\bbox[#dcff8c]{y\text{값}}$의 비율$\\[1em]$
$\dfrac{\bbox[#dcff8c]{y}}{\bbox[#ffff00]{x}} \;\xrightarrow[]{x,\;y\;\text{값}\;\bbox[#ffc5fd]{\square}\text{배}\;}\dfrac{\bbox[#dcff8c]{y} \times \bbox[#ffc5fd]{\square}}{\bbox[#ffff00]{x}\times \bbox[#ffc5fd]{\square}} = \dfrac{y}{x}\; \text{일정}$
정비례 관계식
사탕 $1$개의 가격이 $300$원이라고 할 때 사탕 $x$ 개를 구매하고 지불해야 하는 금액 $y$ 에 대하여 정비례 관계식을 구하는 방법에 대해 알아보자.
- $x:y=1:300=2:600\;\cdots$ 일정 ( 정비례 성질)
- 관계식 : $y=300x$
위의 내용을 바탕으로 정비례 관계식을 일반형으로 표현해 보자.
정비례 일반형 관계식
위의 사실을 통해 $x,\;y$가 정비례 관계이면 두 변수 사이의 비율($\dfrac{y}{x}$)이 일정한 값을 갖는다는 것을 알 수 있다. 이를 수식으로 정리하면 다음과 같다.
$\dfrac{y}{x}=a \; (a\neq 0\;:\;\text{상수, 일정})$
따라서 정비례 관계식의 일반형은 다음과 같다.
- 정비례 일반형 : $y=ax\;(a\neq 0\;:\;\text{상수})$
이제 함수 $y=ax$의 그래프를 그리고 그래프의 성질에 대해 정리해 보기로 하자.
정비례 그래프
정비례 관계식 $y=ax$ 를 이용해 대응표를 채우고 그래프를 그려 성질을 정리해 보자.
$y=ax\;\;(a>0)$ 그래프
$y=ax\;(a>0)$의 그래프를 그리는 과정을 $y=2x,\; y=x,\; y=\dfrac{1}{2}x$를 이용해 살펴보면 다음과 같다.
그래프 그리기
1단계 : 대응표 그리기
먼저 그래프를 쉽게 그리기 위해 아래의 대응표를
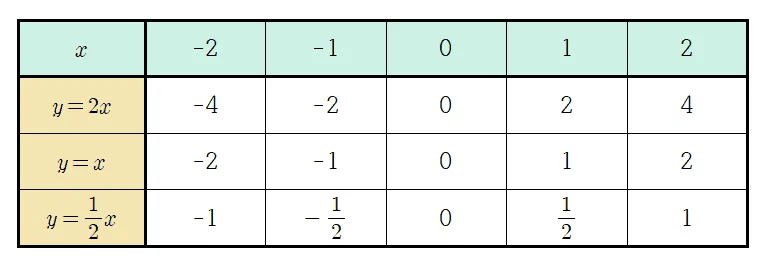
2단계 : 순서쌍 만들기
대응표를 이용해 $(x,y)$의 순서쌍을 만든다.
3단계 : 점찍기
순서쌍을 이용해 점을 찍고, $x$값을 확장하면 유리수를 대입하면 대응표에 주어진 $x$값들 사이에 무수히 많은 $x$값을 추가할 수 있다. 유리수까지 고려하여 점을 찍으면 그래프는 아래와 같은 직선이 됨을 알 수 있다.
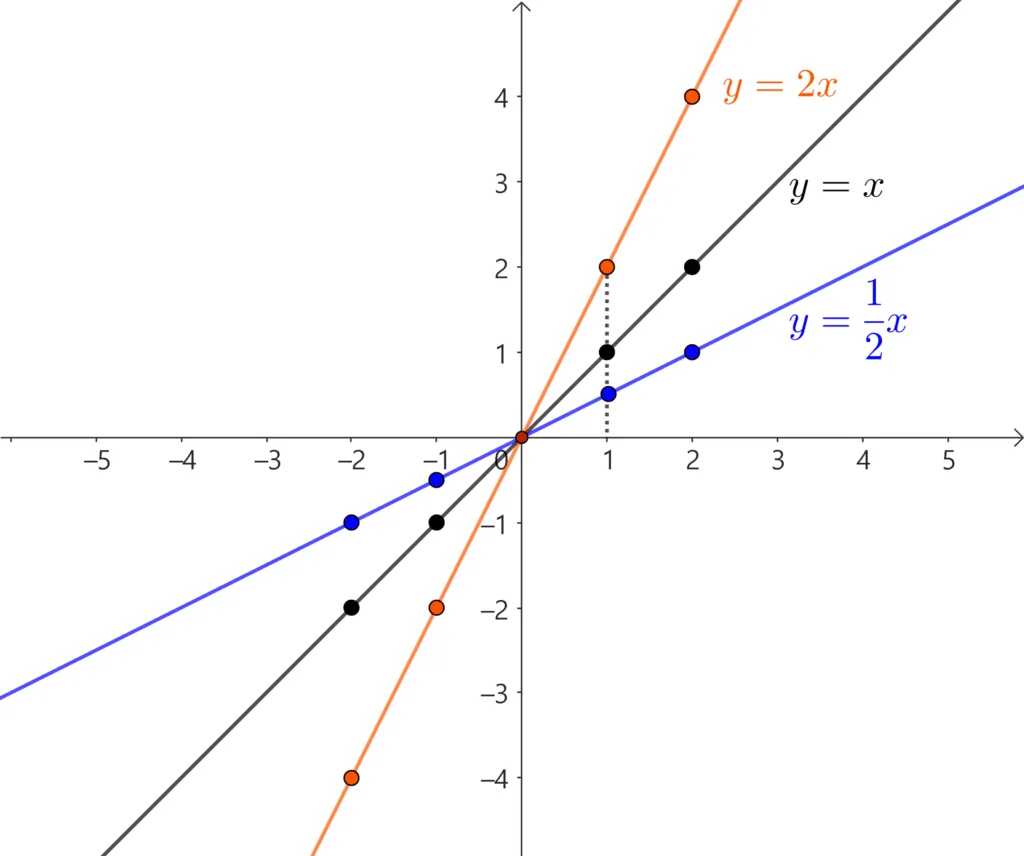
$y=ax\;\;(a<0)$ 그래프
이번에는 $y=ax\;(a<0)$의 그래프를 그리는 과정을 $y=-2x,\; y=-x,\; y=-\dfrac{1}{2}x$를 이용해 살펴보자.
그래프 그리기
그래프를 그리는 과정은 위와 동일하다. 그래프를 그리는 것이 익숙해 졌다면 순서쌍을 구하는 과정은 생략하고 대응표를 이용해 바로 좌표평면에 점을 찍어 그려보기로 하자.
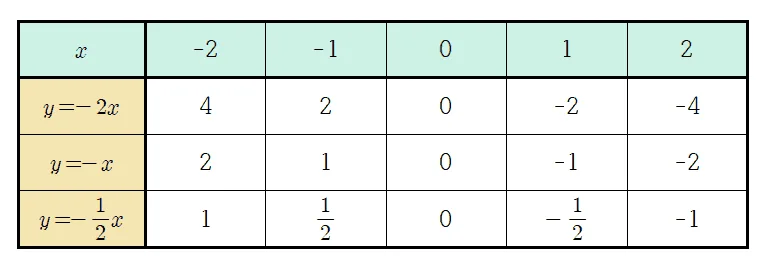
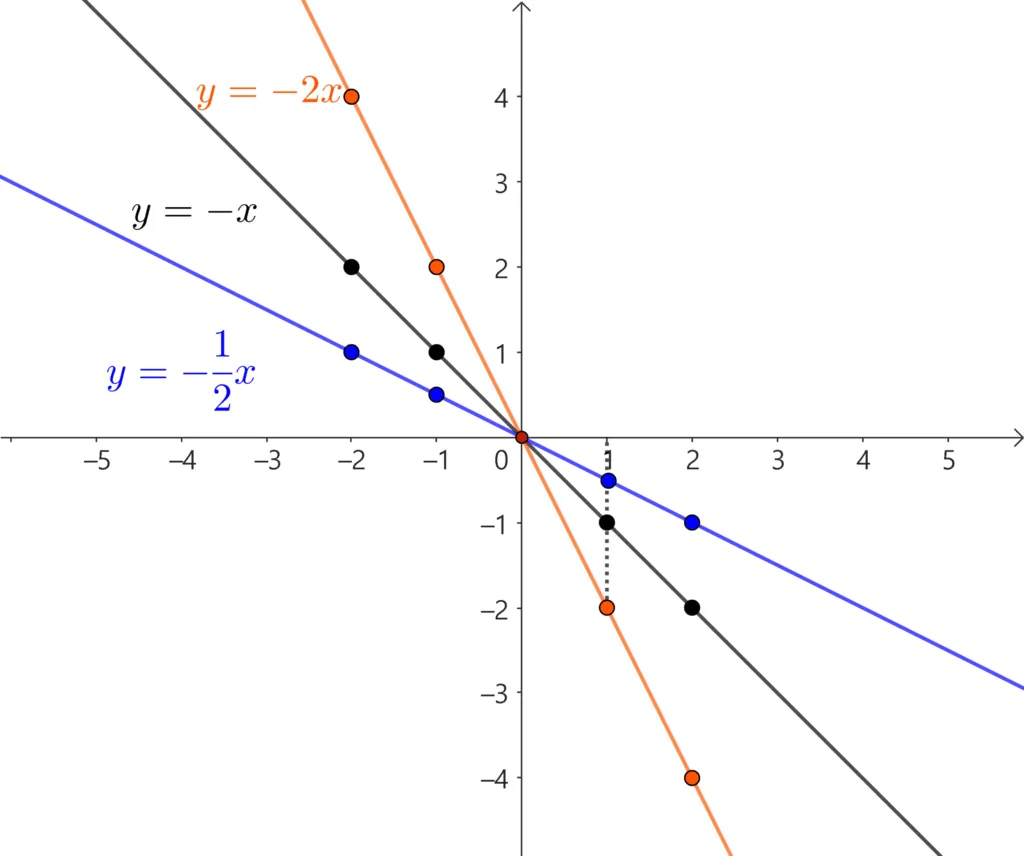
앞서 그려본 $y=ax\; (a\neq0)$의 그래프를 통해 성질을 정리해 보자.
$y=ax$ 그래프 성질
$a>0,\; a<0$일 때 그래프의 성질을 표로 정리 하면 다음과 같다.
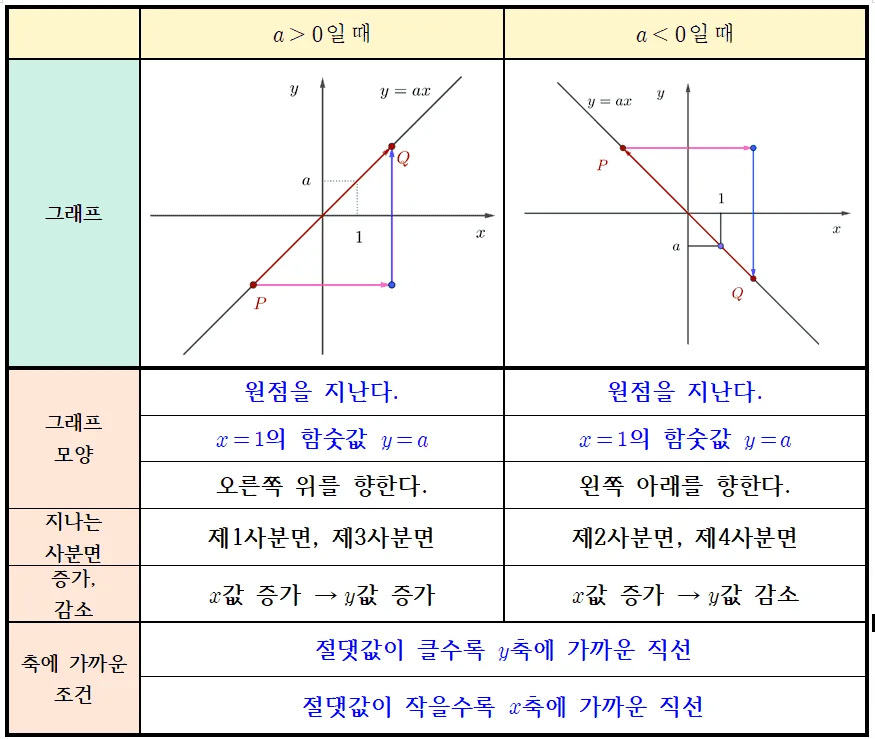
공통성질
$y=ax\;(a\neq0)$의 그래프는 $a$의 부호와 관계 없이 다음과 같은 성질을 갖는다.
- 원점을 지난다.
- $x=1$에서 함숫값은 $y=a$이다.
- $a$의 절댓값이 클수록 $y$축에 가깝다.
- $a$의 절댓값이 작을수록 $x$축에 가깝다.
정리
정비례의 정의
- $x$값이 $2$배, $3$배, $4$배, $\cdots $ 됨에 따라
$y$값도 $2$배, $3$배, $4$배 $\cdots$ 가 되는
$\bbox[#ffff00]{\text{함수}}$관계
정비례의 성질
- $x:y=(\text{일정한 비})$
- $\dfrac{y}{x}=\text{일정 비율}\rightarrow a\;: \text{상수}$
정비례의 일반형 관계식
- $y=ax\;(a\neq0)$
이상으로 정비례에 대한 정리를 마무리 하도록 하겠다.
