접선의 길이는 단순한 수식 암기를 넘어 문제 해결력을 길러주는 핵심 개념입니다. 특히 삼각형이나 사각형에 내접한 원을 활용한 문제에서는 접선의 길이 성질이 결정적인 역할을 하죠. 이번 시간에는 내접원과 외접원의 접선 성질을 중심으로, 다양한 문제 유형을 정리하고 풀이 전략을 익혀보겠습니다.
목차
학습목표
이번 시간에는 접선의 길이에 대한 성질을 이용해 문제를 풀어보려고 한다. 적당한 값을 미지수로 설정하고 수학적인 사실 적용하여 방정식을 만들고 방정식을 풀어 문제를 해결하는 수학적인 사고에 익숙해 지는 시간이 되길 바란다.
- 원에 외접하는 삼각형과 사각형에서 접선의 길이 성질을 적용해 문제를 해결할 수 있다.
복습
이 시간 내용을 이해 하기 위해서는 접선의 길이에 대한 성질을 알아야 한다. 복습이 필요한 학생은 아래의 링크를 이용해 내용을 확인하고 학습하길 바란다.
기본 개념
원 밖의 한 점에서 그은 두 접선이 수직일 때
- 원 $O$ 밖의 한 점 $B$에서 그은 두 접선이 원과 만나는 접점이 $A, C$라 할 때 반지름과 접선으로 만들어진 $\square{ABCO}$는 정사각형이다.

- 접선과 반지름 사잇각: $\angle{OAP}=\angle{OBP}=90^{\circ}$
- 반지름: $\overline{OA}=\overline{OB}$
따라서 $\square{APBO}$는 정사각형이다.
접선의 길이 문제
직각 삼각형과 내접원 반지름 문제
[문제] 직각 삼각형 $\triangle{ABC}$ 의 내심$I$에 대하여 내접원의 반지름의 길이를 구해라.

- $\square{RBPI}$가 정사각형: $\overline{BR}=\overline{BP}=r$
- 접선의 길이: $\overline{AR}=\overline{AQ}=8-r$, $\overline{CP}=\overline{CQ}=6-r$
- $\overline{AC}=\overline{AQ}+\overline{CQ}=(8-r)+(6-r)=10$, $\therefore r=2$
외접 사각형과 접선의 길이 문제
[문제] $\angle{A}=\angle{B}=90^\circ$이고 원에 외접하는 $\square{ABCD}$와 내접원 $O$와 접하는 접점 $E, F, G, H$에 대하여 $\overline{AB}=8$, $\overline{BC}=12$일 때 $\square{ABCD}$의 둘레를 구하여라.

- $\square{AFOE},\square{FBGO}$: 정사각형
- $\overline{ED}=x$로 두면 $\overline{ED}=\overline{DH}=\overline{GH}=x$
- $\overline{CG}=\overline{CH}=8$, $\overline{HC}=8-x$
- $\triangle{DHC}$: $(x+8)^2=8^2+(8-x)^2$, $x=2(\because x>0)$
- [$\square{ABCD}$둘레] $=36$
반원과 접선의 길이 문제
위의 문제에서 반원을 제거하면 아래와 같은 문제로 변형 할 수 있다.
[문제] 사각형 $\square{EDCG}$에서 $\overline{OG}=2$, $\overline{DC}=5$일 때 $\triangle{DOC}$의 넓이와 둘레를 구하여라.

$\triangle{DOC}$의 넓이 구하기
- $\triangle{DOC}=\frac{1}{2}\times\overline{DC}\times\overline{OH}=\frac{1}{2}\times5\times2=5$
$\triangle{DOC}$의 둘레 구하기
- $\overline{ED}=x$라 두면, $\overline{ED} =\overline{DH}=\overline{DP}=x$
- $\triangle{DPC}$: $\overline{DP}=4,\overline{DC}=5$이므로 $\therefore \overline{PC}=3$
- $\overline{GC}=\overline{CH}=3+x$
- $\overline{CD}=\overline{CH}+\overline{DH}=2x+3=5$, $\therefore x=1$
- $\overline{DO}=\sqrt{5}$, $\overline{OC}=2\sqrt{5}$
- [$\triangle{DOC}$의 둘레] $=5+3\sqrt{5}$
또한 여기서 한 가지 기억하고 넘어갈 사실은 다음과 같다.
- $\angle{EOD}=\angle{HOD},\angle{COH}=\angle{COG}$, $\therefore\angle{DOC}=90^\circ$
- $\triangle{OED}\sm\triangle{CGO}$
닮음을 이용한 문제도 출제 될 수 있으니 성질을 꼭 기억해 두도록 하자.
사분원과 접선의 길이 문제
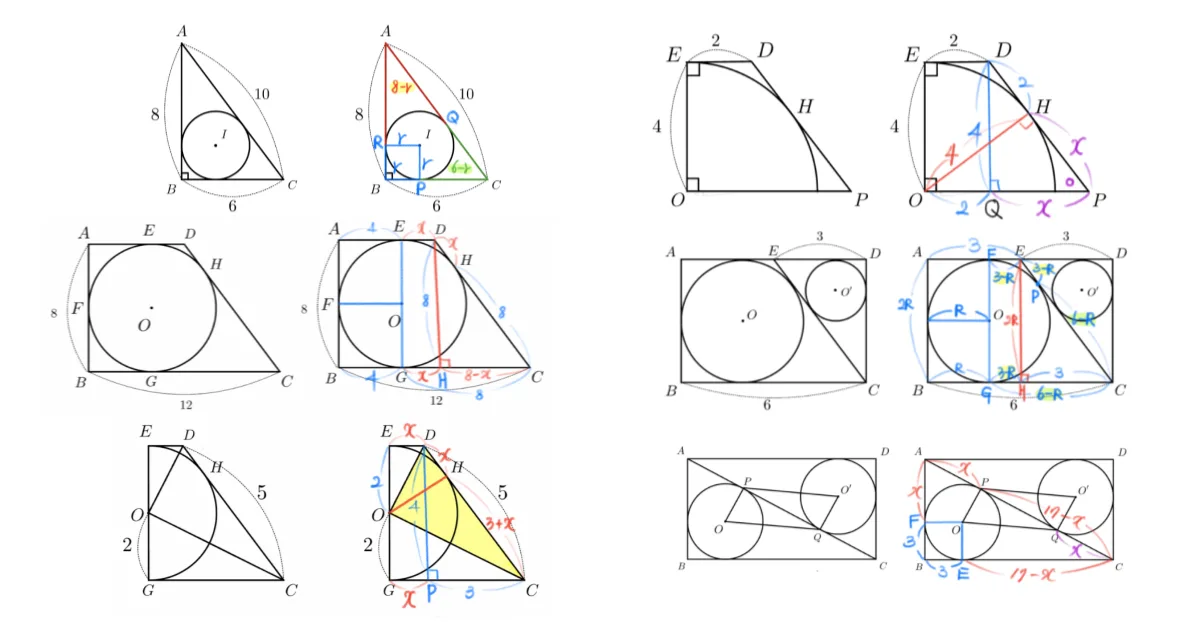
[문제] 위의 사각형에서 반원의 중심 $O$를 지나고 $\overline{GC}$와 평행한 직선으로 잘라 만든 사분원과 $\square{EODP}$에 대하여 $\overline{OE}=4$, $\overline{ED}=2$일 때 $\overline{OP}$를 구하여라.

- $\triangle{OHP}\equiv\triangle{DQP}$ ($SAS$ 합동), $\overline{QP}=\overline{HP}$
- $\triangle{DQP}$ : $4^2+x^2=(2+x)^2$, $x=3$ ($\because x>0$) $\therefore\overline{OP}=5$
사분원에 대한 풀이 과정에서 기억할 사실은 원의 중심에서 접점까지 연결한 보조선 $\overline{OP}$과 점 $D$에서 $\overline{OP}$에 그은 수선 $\overline{DQ}$로 다음의 합동인 삼각형을 찾는 과정이다.
- $\triangle{PQD}\equiv\triangle{PHO}$
이제 접선의 길이에 대한 심화 문제를 학습해 보기로 하자.
접선의 길이 심화 문제
외접 삼각형과 외접 사각형 혼합문제
[문제] 직사각형 $\square{ABCD}$의 한 변 $\overline{AD}$의 중점 $E$와 $\overline{EC}$에 접하는 두 원 $O,\, O’$의 반지름 $R,\,r$의 값을 구하여라.

- $\overline{GC}=\overline{CP}=6-R$, $\overline{EF}=\overline{EP}=\overline{GH}=3-R$
- $\triangle{EHC}$ : $2R^2+3^2=(9-2R)^2$ , $R=2 (\because R>0)$
$r$을 구하는 두 가지 방법

풀이1 : 첫 번째 문제와 동일한 풀이 과정 적용
풀이2 : $\triangle{FBC}\equiv\triangle{CDE}$ 이므로 $R:r=2:1(\because 닮음비)$ $\therefore r=1$
이 문제에서 핵심은 $R$부터 구해야 한다는 사실이다. 사각형에 주어진 길이 조건은 2개이고, 삼각형은 1개 뿐이기 때문이다. 또 하나 주목할 사실은 $r$을 구하는 두번째 풀이 과정이다. 문제의 조건만 가지고 $R:r=2:1$임을 알 수 있다는 점을 기억하자.
합동인 두 외접 직각삼각형에 대한 심화 문제
[문제] 사각형 $\square{ABCD}$을 대각선 $\overline{AC}$로 나누어진 합동인 두 삼각형의 내접원 $O, O’$이 있다. 원과 $\overline{AC}$의 접점 $P, Q$에 대하여, $\square{ABCD}$의 둘레가 46, 원의 반지름이 3일 때 $\square{OPO’Q}$의 넓이를 구하여라.

$\overline{AP}=\overline{AF}=x$에 대하여
- $\overline{AB}+\overline{BC}=23$ , $\overline{CE}=17-x$
- $\triangle{ABC}$ : $(x+3)^2+(20-x)^2=17^2 \;,\; x=12\;또는\;x=5$
- $\overline{AB}<\overline{BC}$ 이므로 $x\neq12$ , $x=5$
- $\overline{AP}=\overline{QC}=5\;(\because\triangle{ABC}\equiv\triangle{CDA})$ , $\overline{PQ}=7$
- [$\square{POQO’}$의 넓이]$=\overline{OP}\times\overline{PQ}=21$ $(\because \overline{OP}\perp\overline{PQ})$
이상으로 접선의 길이에 대한 심화 문제 풀이를 마무리 하고 접선의 길이와 관련된 문제를 해결하는 요점을 정리하고 마치도록 하자.
문제 해결의 KEY
접선의 길이와 관련된 문제는 대부분 직각삼각형을 이용한 이차방정식 풀이로 귀결된다. 따라서 다음의 과정이 중요하다.
- 문제에서 구해야 하는 값이 무엇인지 확인하기.
- 어떤 보조선이 필요 한지 찾기. (직각삼각형)
- 구해야 하는 값을 $x$로 두고, 접선의 성질을 이용해 세 변의 길이를 한 문자 $x$로 표현하기
- 일차 방정식, 피타고라스 정리 적용한 이차방정식을 세우고 방정식을 풀기.
이를 명심하고 문제를 풀어보고 사고과정에 익숙해 지도록 하자.