이번 시간에는 수직선을 이용해 절댓값과 수의 대소관계에 대해 정리해 보자.
목차
수직선
먼저 정수를 수직선에 표현하는 방법에 대해 알아보자. 수직선은 오른쪽으로 갈수록 커지고 왼쪽으로 갈수록 적어진다. 자연수 1부터 하나씩 감소하는 수 $0,-1,-2,-3,\dots$를 순서대로 왼쪽에 나열하면 정수를 다음과 같이 나타낼 수 있다.
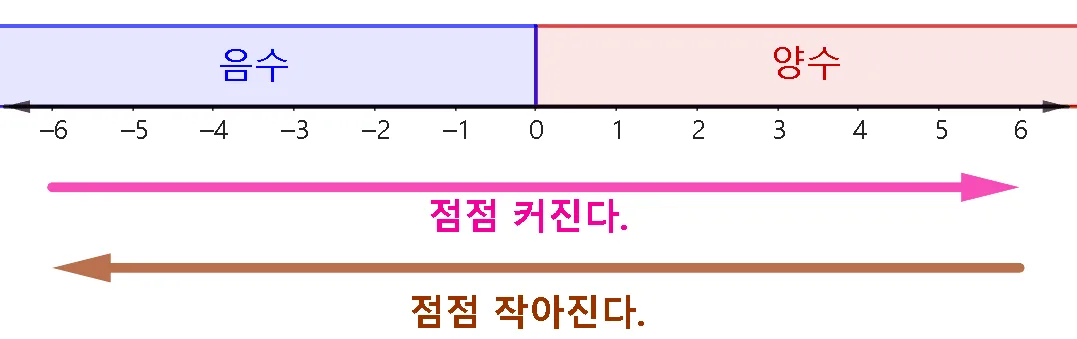
수직선에서 0을 기준으로 오른쪽에 있는 수를 양수, 왼쪽에 있는 수를 음수라고 한다. 그리고 0은 양수도 음수도 아니다. 이제 유리수를 수직선에 표현하는 방법에 대하여 살펴보자.
간단한 유리수$-\dfrac{1}{2},-\dfrac{7}{3}$을 수직선에 표현하는 방법에 대하여 살펴보자. 양의유리수 $\dfrac{1}{2},\dfrac{7}{3}$과 크기는 같고 정확히 반대되는 양을 가지고 있는 값이므로 아래와 같이 ‘$0$’에서 같은 거리에 표현 할 수 있다.
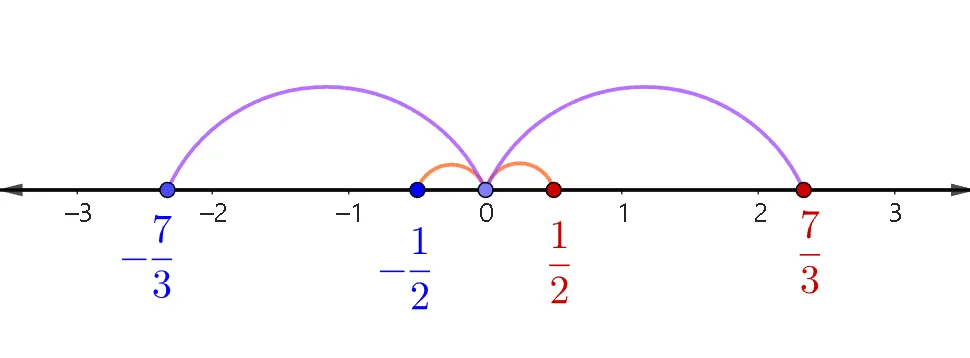
수직선에서 두 음의유리수 $-\dfrac{1}{2},-\dfrac{7}{3}$의 위치를 비교해 크기를 비교하면 $-\dfrac{1}{2}>-\dfrac{7}{3}$임을 알 수 있다.
이를 통해 두 음수를 비교할 때 원점에서 떨어진 거리가 멀면 더 작다는 사실을 알 수 있다. 학습을 잠깐 멈추고, ‘절댓값’이란 용어를 도입하고 수의 대소관계를 다시 정리해 보기로 하자.
절댓값과 수의 대소관계
절댓값
절댓값의 정의
- 절댓값 : 수직선 위의 어떤 수를 나타내는 점과 $0$(원점)사이의 거리
- 기호 : $|\;\square\;|$
- 예시 : $|2|=2,\;|-3|=3,\;\left|-\dfrac{1}{2}\right|=\dfrac{1}{2}$
절댓값은 부호를 제거한 수이다.
절댓값의 의미를 생각할 때는 거리를 생각하고, 계산할 때는 부호를 제거한 수로 계산하자.
절댓값의 성질
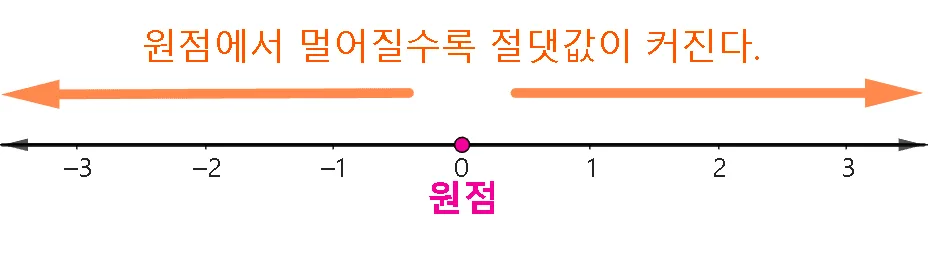
- 원점에서 멀어질수록 절댓값이 커지고
원점에 가까워질수록 절댓값이 작아진다. - 절댓값은 0 또는 양수이다.
절댓값이 0인 수는 0 뿐이다. - 절댓값이 $\bbox[#ffff00]{\text{양수}}$인 수: $+\bbox[#ffff00]{\text{양수}},-\bbox[#ffff00]{\text{양수}}$
[예시] $|\square|=3$이면 $\square=-3 \;or +3$
절댓값의 범위표현
$a>0$에 대하여 다음이 성립한다.
| 절댓값 식 | 풀이 |
|---|---|
| $|x|<a$ | $-a<x<a$ |
| $|x| \leq a$ | $-a \leq x \leq a$ |
| $|x|>a$ | $x<-a\;\text{or}\;x>a$ |
| $|x| \geq a$ | $x \leq -a\;\text{or}\; x \geq a$ |
| $|x| = a$ | $x = -a\;\text{or}\;x=a$ |
수의 대소관계
수직선과 절댓값을 이용해 수의 대소관계를 정리해 보기로 하자.
- 수직선: 오른쪽으로 갈수록 커지고, 왼쪽으로 갈수록 작아진다.
- $\bbox[#94feff]{\text{음수}}<0<\bbox[#ffff00]{\text{양수}}$
- $\bbox[#ffff00]{\text{두 양수}}$: 절댓값이 클수록 크다.
- $\bbox[#94feff]{\text{두 음수}}$: 절댓값이 클수록 작다.
| $x>2$ | $x<2$ | $x\geq2$ | $x\leq2$ |
|---|---|---|---|
| $\square>2$ | $\square<2$ | $\square\geq2$ | $\square\leq2$ |
| $\square$는 $2$보다 크다. | $\square$는 $2$보다 작다. | $\square$는 $2$보다 크거나 같다. | $\square$는 $2$보다 작거나 같다. |
| $\square$는 $2$ 초과 | $\square$는 $2$ 미만 | $\square$는 $2$ 이상 | $\square$는 $2$ 이하 |
| $\square$는 $2$보다 작지 않다. | $\square$는 $2$보다 크지 않다. |
이상으로 절댓값과 수의 대소관계에 대해 정리해 보았다.
