이번 시간에는 작도와 삼각형의 합동조건에 관련된 문제를 정리해 보려고 합니다. 합동과 관련한 문제는 대칭과 회전이동에 밀접하게 관련되어 있으므로 이를 중심으로 정리해 보도록 하겠습니다.
목차
작도 문제
평행선의 작도 순서
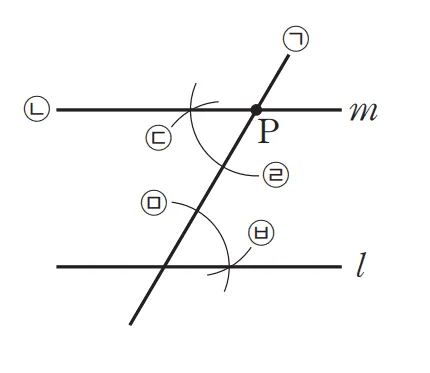
다음은 $l$위에 있지 않은 점 $P$를 지나고 $l$에 평행한 직선 $m$을 작도한 것이다. 작도과정을 순서대로 나열하여라.
[풀이]
평행선을 엇각을 이용해 작도하는 과정으로 교점을 만들기 위해 직선($ㄴ$)을 그리고 크기가 같은 각을 엇각으로 작도하면 된다.
$ㄱ \rightarrow ㅁ \rightarrow ㄹ \rightarrow ㅂ \rightarrow ㄷ\rightarrow ㄴ$
삼각형의 작도
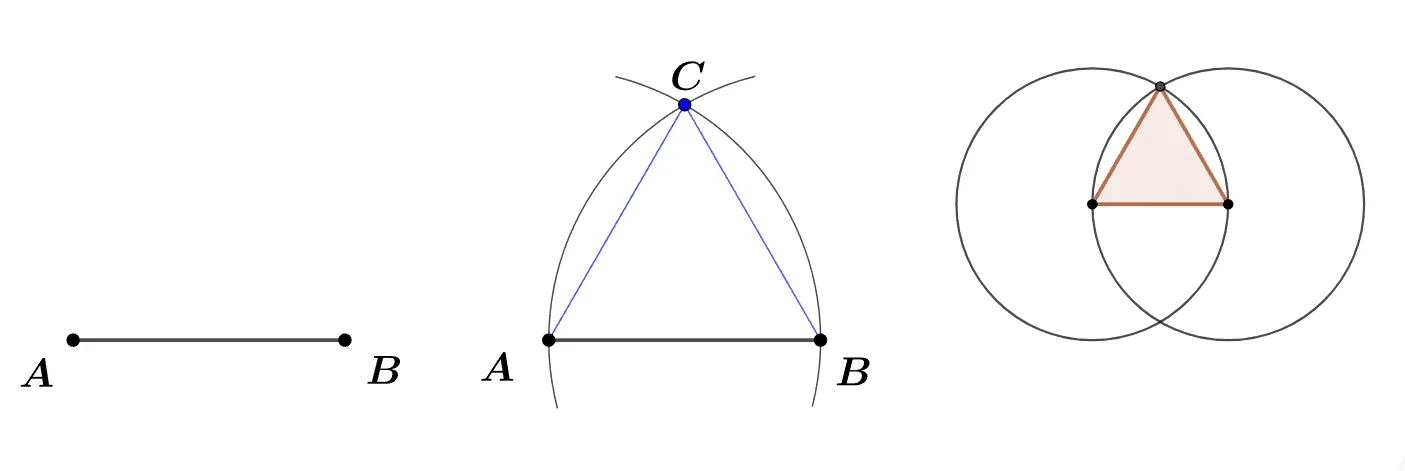
주어진 선분 AB의 양 끝점 $A,\;B$에서 반지름이 $\overline{AB}$인 원을 그려 만나는 점을 $C$라고 할 때 $\triangle{ABC}$는 어떤 삼각형이 되는지 설명하여라. (세 번째 그림은 문제와 관련없는 보충자료)
[풀이]
$\overline{AB}=\overline{AC}=\overline{BC}=\text{(반지름)}$이고 따라서 $\triangle{ABC}$는 정삼각형이다.
이 문제를 통해 알 수 있는 사실은 원의 중심이 원의 둘레에 오도록 반직름이 같은 두 원을 겹치면 정삼각형이 만들어 진다는 것이다.
직각의 삼등분선 작도
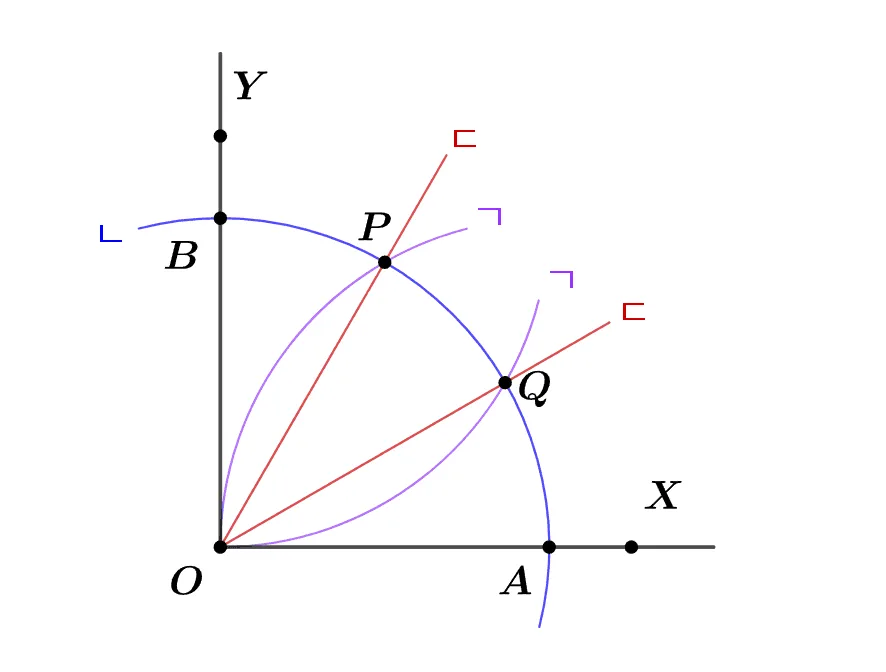
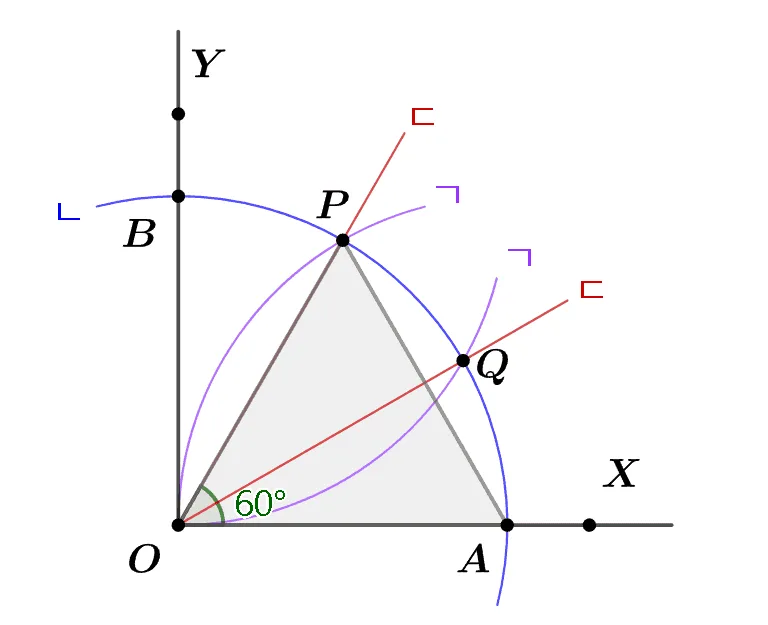
다음의 그림에서 ㄱ, ㄴ, ㄷ은 $\angle{XOY}=90^\circ$를 삼등분하는 작도 과정이다. 작도과정을 순서대로 나열하고, 삼등분 되는 이유를 설명하여라.
[풀이]
정삼각형을 이용해 직각을 삼등분하는 작도 이다. 작도 순서는 $\text{ㄴ} \rightarrow\text{ㄱ} \rightarrow\text{ㄷ}$이다.
$\triangle{POA}, \triangle{BOQ}$는 정삼각형이고 따라서 $\angle{BOP}=\angle{QOA}=30^\circ$이다. 이는 $\angle{POQ}=30^\circ$임을 의미하고 ‘ㄷ’ 은 직각$\angle{XOY}$의 삼등분선이다.
삼각형의 결정조건
삼각형이 하나로 결정되는지 판단하고, 하나로 결정 되지 않으면 그 이유를 서술하시오.
- $\overline{AB}=3$, $\overline{BC}=4$, $\overline{CA}=5$
- $\overline{AB}=4$, $\overline{BC}=3$, $\overline{CA}=7$
- $\overline{BC}=6$, $\overline{CA}=7$, $\angle{A}=30^\circ$
- $\overline{BA}=4$, $\overline{BC}=3$, $\angle{B}=120^\circ$
- $\overline{CA}=7$, $\angle{B}=30^\circ$, $\angle{C}=60^\circ$
- $\overline{BC}=6$, $\angle{B}=120^\circ$, $\angle{C}=60^\circ$
- $\overline{AC}=10$, $\angle{A}=45^\circ$, $\angle{C}=60^\circ$
- $\angle{A}=30^\circ$, $\angle{B}=60^\circ$, $\angle{C}=90^\circ$
[풀이]
1, 2 : 세 변의 길이가 주어진 경우이고, $(\text{가장 긴 변})<(\text{나머지 두 변의 합})$을 만족해야 삼각형이 하나로 결정된다. 따라서 2번은 하나로 결정되지 않는다.
3, 4 : 두 변의 길이와 한 각이 주어진 경우이다. 이 때 주어진 각이 끼인각일 때 하나로 결정된다. 따라서 3번은 하나로 결정되지 않는다.
5 : 나머지 한 각의 크기 $\angle{A}=90^\circ$를 이용해 하나로 결정지을 수 있다. 반면에 $7,\;30^\circ,\;60^\circ$로 주어졌다면 삼각형은 하나로 결정되지 않는다.
6, 7 : 한 변의 길이와 두 각이 주어진 경우이다. 이 때 두 각 은 주어진 선분의 양 끝 각 이면서 각의 합이 $180^\circ$보다 작은 7은 하나로 결정된다. 따라서 6은 하나로 결정 되지 않는다.
8 : 세 각이 주어진 경우는 두 각만 주어진 경우와 같고 평행선을 이용해 무수히 많은 삼각형을 만들 수 있기 때문에 하나로 결정되지 않는다.
세 변의 길이 조건
다음 조건을 만족하는 삼각형의 개수를 구하여라.
- 둘레의 길이 12
- 각 변의 길이는 자연수
[풀이]
$(\text{긴 변의 길이})\bbox[#ffff00]{<}(\text{나머지 두 변의 길이 합})$을 이용해 긴 변의 길이를 기준으로 생각해보자.
$(\text{긴 변의 길이})\bbox[#dcff8c]{=}(\text{나머지 두 변의 길이 합})$ 경우 양쪽의 값이 $\bbox[#dcff8c]{6}$이고 이 때는 삼각형을 만들 수 없다. 좌변이 작아지면 우변이 커지므로 위의 가장 긴 변의 길이가 $\bbox[#dcff8c]{6}$보다 작은 경우만 고려하면 된다.
둘레의 길이가 12가 되는 $\bbox[#ffff00]{\text{가장 긴 변}}$과 $\bbox[#dcff8c]{\text{나머지 두변의 길이의 합}}$ 은 다음과 같다.
- $(\bbox[#ffff00]{5},\bbox[#dcff8c]{7}),\;(\bbox[#ffff00]{4},\bbox[#dcff8c]{8})$
- $(\bbox[#ffff00]{3},\bbox[#dcff8c]{9})\cdots$ : 두 변의 길이 합이 9가 되면 3이 가장 긴변이 될 수 없음.
따라서 $(\bbox[#ffff00]{5},\bbox[#dcff8c]{7}),\;(\bbox[#ffff00]{4},\bbox[#dcff8c]{8})$에 대해서만 고려하면 된다.
$\bbox[#ffff00]{5}\rightarrow\bbox[#dcff8c]{7}
\begin{cases} (1,\bbox[#ffc5fd]{6}): \bbox[#ffff00]{5}\text{보다 큰 수}\\[1em]
(\bbox[#dcff8c]{2,5})\rightarrow \bbox[#ffff00]{5},\bbox[#dcff8c]{2,5} \\[1em]
(\bbox[#dcff8c]{3,4})\rightarrow \bbox[#ffff00]{5},\bbox[#dcff8c]{3,4}\\[1em]
(\bbox[#ffc5fd]{4,3}) : \text{중복된 경우} \\[1em]
\cdots\end{cases}$
비슷한 방법으로 $(\bbox[#ffff00]{4},\bbox[#dcff8c]{8})$을 고려하면 다음과 같다.
$\bbox[#ffff00]{4}\rightarrow\bbox[#dcff8c]{8}
\begin{cases} \cdots \\[1em]
(3,\bbox[#ffc5fd]{5}): \text{긴 변 오류}\\[1em]
(\bbox[#dcff8c]{4,4})\rightarrow \bbox[#ffff00]{4},\bbox[#dcff8c]{4,4}\\[1em]
(\bbox[#ffc5fd]{5,3}) : \text{중복된 경우}\\[1em]
\cdots \end{cases}$
따라서 조건에 맞는 삼각형은 $(\bbox[#ffff00]{5},\bbox[#dcff8c]{2,5})$, $(\bbox[#ffff00]{5},\bbox[#dcff8c]{3,4})$, $(\bbox[#ffff00]{4},\bbox[#dcff8c]{4,4})$ 3개이다.
삼각형의 합동조건
$\overline{AB}=\overline{FD}$ 일 때 $\triangle{ABC}\equiv\triangle{FDE}$가 되기 위해 필요한 최소 조건을 모두 찾아라.
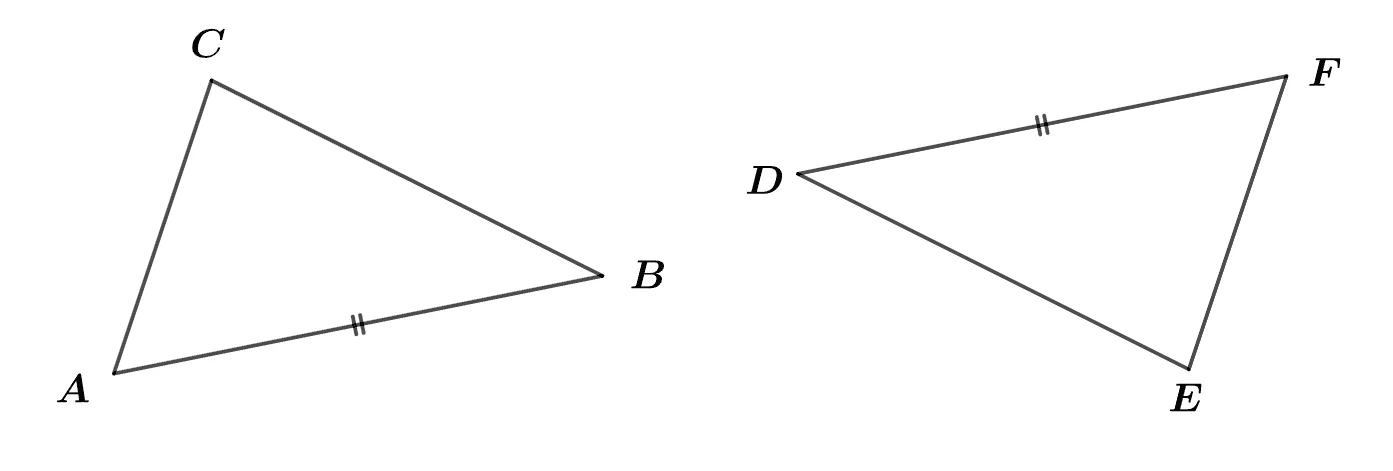
[풀이]
$\triangle{ABC}\equiv\triangle{FDE}$을 만족하는 최소조건을 합동 조건에 따라 나누어 정리하면 다음과 같다.
- SSS 합동
- $\overline{BC}=\overline{DE}$, $\overline{CA}=\overline{EF}$
- SAS 합동
- $\overline{BC}=\overline{DE}$, $\angle{B}=\angle{D}$
- $\overline{CA}=\overline{EF}$, $\angle{A}=\angle{F}$
- ASA 합동
- $\angle{A}=\angle{F}$, $\angle{B}=\angle{D}$
- $\angle{B}=\angle{D}$, $\angle{C}=\angle{E}$
- $\angle{C}=\angle{E}$, $\angle{A}=\angle{F}$
사다리꼴 넓이 증명
$\overline{BC}\pa\overline{AD}$인 사다리꼴 $\square{ABCD}$에 대하여 점 $A$와 $\overline{CD}$의 중점 $M$을 지나는 직선이 직선 BC와 만나는 점을 $P$라고 할 때 사다리꼴의 넓이를 구하는 공식을 유도하여라.
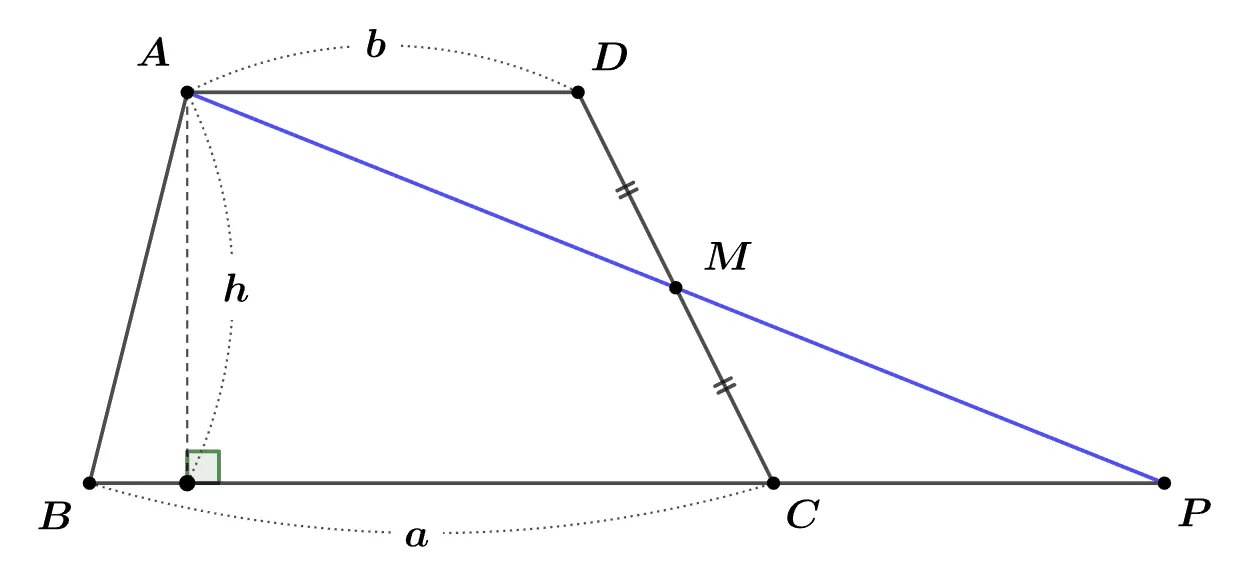
[풀이]
- $\triangle{MDA}\equiv\triangle{MCP}$
- $\overline{MD}=\overline{MC}$ : 문제 조건
- $\angle{DMA}=\angle{CMP}$ : 맞꼭지각
- $\angle{MDA}=\angle{MCP}$ : 엇각
따라서 $\overline{AD}=\overline{CP}=b$, $\triangle{MDA}=\triangle{MCP}$이다.
$\begin{align}\square{ABCD}&=\triangle{ABP}\\[1em]
&=\dfrac{1}{2}\times (\overline{BC}+\overline{CP})\times h\\[1em]
&=\dfrac{1}{2}\times(a+b)\times h(\because\;\overline{AD}=\overline{CP})\\[1em]
&=\dfrac{a+b}{2}\times h\end{align}$
Q.E.D.
대칭과 회전을 이용한 합동
포개어 겹쳐지는 도형을 합동이라고 한다. 수학에서 두 도형을 겹치는 원리는 대칭과 평행이동을 이용한다. 따라서 합동에 관련한 문제의 대부분은 대칭성이 있는 도형을 가지고 출제되거나 이를 회전한 도형으로 주어진다. 이를 잘 파악하고 있으면 문제를 해결하는데 큰 도움이 된다.
대칭인 도형과 합동
예제
정사각형 $\square{ABCD}$에 대하여 표시된 두 삼각형은 합동이다 합동인 이유를 찾고 $x$의 크기를 구하여라.
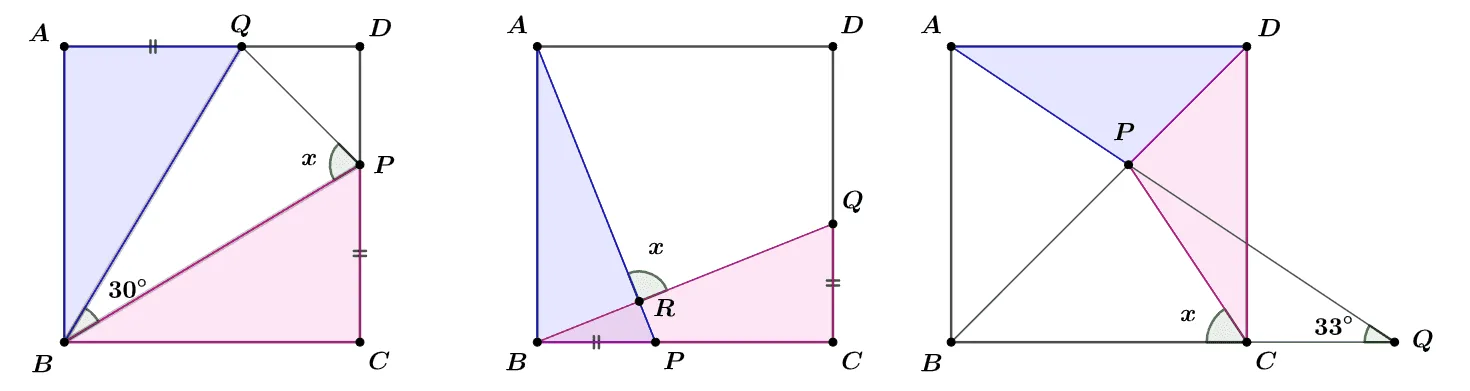
[풀이]
기호를 이용해 다음과 같이 풀이할 수 있다. 풀이과정을 수식으로 정리하는 것은 학생에게 맡기도록 하겠다.
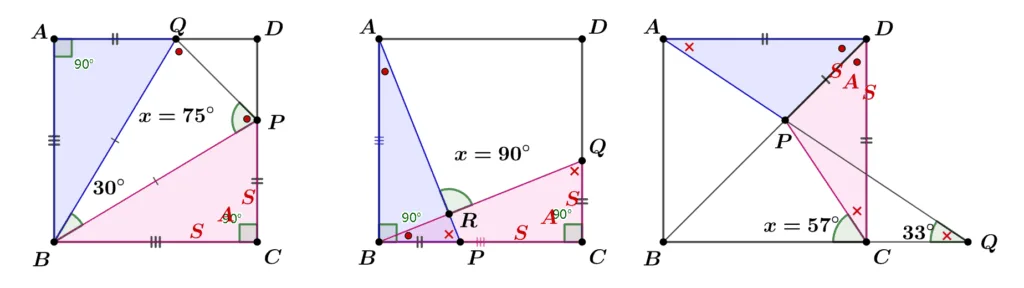
대표 문제
$\overline{AE}=\overline{BF}=\overline{CD}$인 정삼각형 ABC에 대하여 다음을 보여라.
- $\triangle{AED}\equiv \triangle{BFE}\equiv\triangle{CDF}$
- $\triangle{EDF}$는 정삼각형
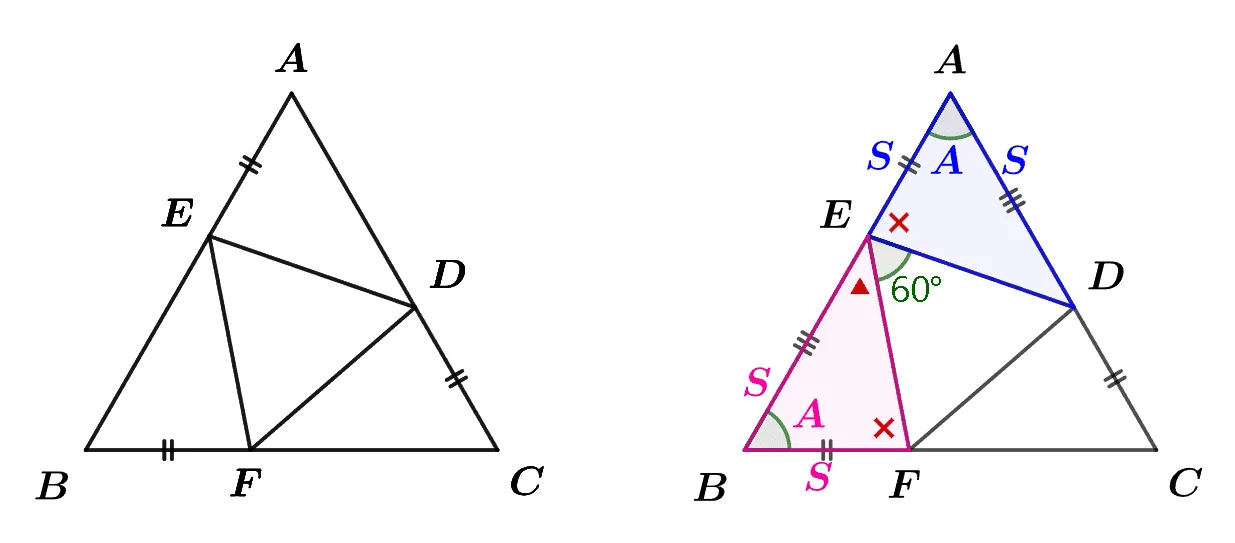
1.[풀이]
- $\overline{AE}=\overline{BF}$ : 조건
- $\overline{AD}=\overline{BE}$
- $\angle{A}=\angle{B}=60^\circ$
따라서 $\triangle{AED}\equiv \triangle{BFE}$ (SAS 합동)이다.
2.[풀이]
- $\angle{AED}=\angle{BFE}=\color{red}\times$
- $\text{(삼각형 내각의 합)}=60^\circ+{\color{red}\blacktriangle}+{\color{red}\times}=180^\circ $
$\angle{FED}=60^\circ$이고 따라서 $\triangle{DEF}$는 정삼각형이다.
심화 문제 정사각형
정사각형 $\square{ABCD}$의 각 변의 중점 $E,\;F,\;G,\;H$에 대하여 다음을 보여라.
- $\triangle{ABF}\bbox[#ffff00]{\equiv}\triangle{CDH}$
- $\triangle{ABQ}\bbox[#dcff8c]{\equiv}\triangle{CDS}$
- $\triangle{BFQ}\bbox[#ffc5fd]{\equiv}\triangle{DHS}$
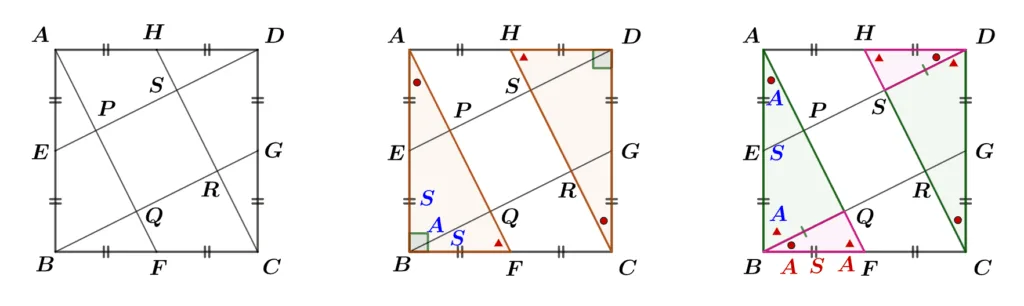
[1] 풀이
- $\overline{AB}=\overline{CD}$: 정사각형
- $\overline{BF}=\overline{DH}$: 문제조건
- $\angle{ABF}=\angle{CDH}=90^\circ$
따라서 $\triangle{ABF}\bbox[#ffff00]{\equiv}\triangle{CDH}$ (SAS 합동)
추가적으로 대응각에 대해 다음이 성립한다.
$\angle{FAB}=\angle{HCD}={\color{red}\bullet}$
$\angle{BFA}=\angle{DHC}=90^\circ-{\color{red}\bullet}={\color{red}\blacktriangle}$
[2] 풀이
$\triangle{ABF}\bbox[#ffff00]{\equiv}\triangle{CDH}$이므로 다음이 성립한다.
- $\angle{BAF}=\angle{DCH}={\color{red}\bullet}$
- $\angle{ABQ}=\angle{CDS}=90^\circ-{\color{red}\bullet}={\color{red}\blacktriangle}$
- $\overline{AB}=\overline{CD}$
$\triangle{ABQ}\bbox[#dcff8c]{\equiv}\triangle{CDS}$ (ASA합동)이다.
[3] 풀이
$\triangle{ABF}\bbox[#ffff00]{\equiv}\triangle{BCG}\bbox[#ffff00]{\equiv}\triangle{CDH}\bbox[#ffff00]{\equiv}\triangle{DAE}$이므로 다음이 성립한다.
- $\angle{GBC}=\angle{EDA}={\color{red}\bullet}$
- $\angle{AFB}=\angle{CHD}={\color{red}\blacktriangle}$
- $\overline{BF}=\overline{DH}$
따라서 $\triangle{BFQ}\bbox[#ffc5fd]{\equiv}\triangle{DHS}$ (ASA 합동)
심화 문제 정삼각형
$\overline{AE}=\overline{BF}=\overline{CD}$인 정삼각형 ABC에 대하여 다음을 보여라.
- $\triangle{ABF}\bbox[#ffff00]{\equiv} \triangle{BCD}\bbox[#ffff00]{\equiv} \triangle{CAE}$
- $\triangle{ABR}\bbox[#dcff8c]{\equiv} \triangle{BCP}\bbox[#dcff8c]{\equiv}\triangle{CAE}$
- $\triangle{AEQ}\bbox[#ffc5fd]{\equiv}\triangle{BFR}\bbox[#ffc5fd]{\equiv}\triangle{CDP}$
- $\triangle{PQR}$은 정삼각형이다
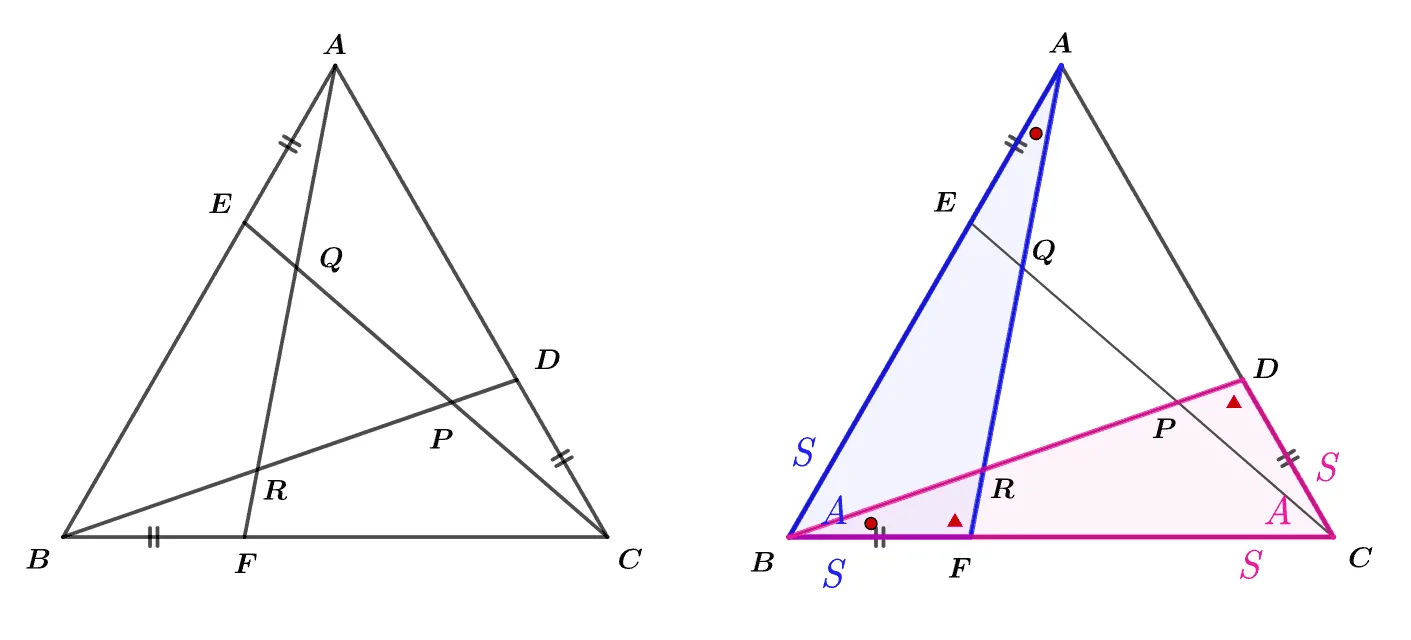
[1] 풀이
- $\overline{BF}=\overline{CD}$ : 조건
- $\overline{AB}=\overline{BC}$ : 정삼각형
- $\angle{ABF}=\angle{BCD}=60^\circ$ : 정삼각형
따라서 $\triangle{ABF} \bbox[#ffff00]{\equiv} \triangle{BCD}$ (SAS합동)이다.
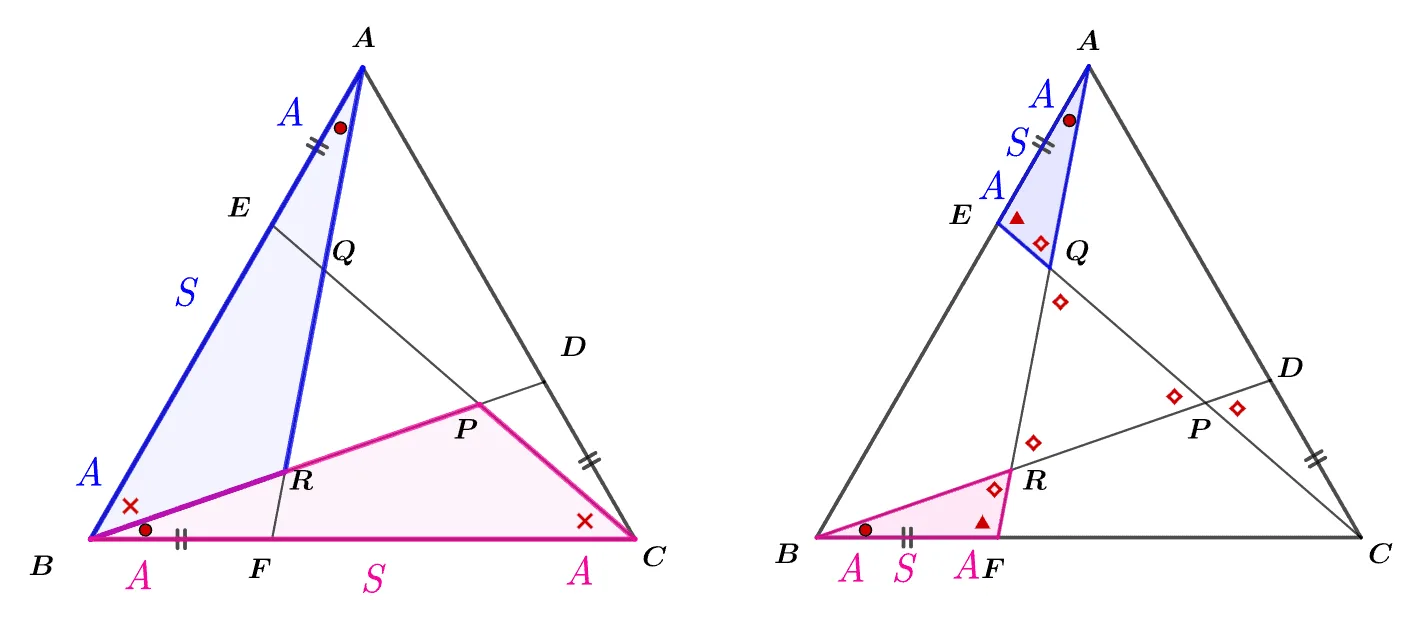
[2] 풀이
$\triangle{ABF}\bbox[#ffff00]{\equiv} \triangle{BCD}\bbox[#ffff00]{\equiv} \triangle{CAE}$ 이므로
- $\overline{AB}=\overline{BC}$ : 정삼각형
- $\angle{BAF}=\angle{CBD}={\color{red}\bullet}$
- $\angle{ABR}=\angle{BCP}=60^\circ-\color{red}\bullet$
따라서 $\triangle{ABR}\bbox[#dcff8c]{\equiv}\triangle{BCP}$는 ASA합동이다.
[3]풀이
$\triangle{ABF}\bbox[#ffff00]{\equiv} \triangle{BCD}$ 이므로
- $\overline{BF}=\overline{CD}$ : 조건
- $\angle{QAE}=\angle{RBF}$
- $\angle{AEQ}=\angle{BFR}$
따라서 $\triangle{AEQ}\bbox[#ffc5fd]{\equiv} \triangle{BFR}$는 ASA합동이다.
[4] 풀이
$\triangle{AEQ}\bbox[#ffc5fd]{\equiv} \triangle{BFR}\bbox[#ffc5fd]{\equiv}\triangle{CDP}$이므로 $\angle{AQE}=\angle{BRF}=\angle{CPD}$ 이고 각각의 맞꼭지각에 대하여 다음이 성립한다.
$\angle{PQR}=\angle{QRP}=\angle{RPQ}=60^\circ$
따라서 $\triangle{PQR}$은 정삼각형이다.
회전과 합동
한 점에서 회전한 형태의 합동인 삼각형을 찾는 문제에 대해 살펴보자.
예제
두 정사각형과 두 정삼각형이 이어져 있을 때 다음과 같이 합동인 삼각형을 고려할 수 있다.
- 겹쳐진 점 $\bbox[#ffff00]{C}$ 에서 $\bbox[#dcff8c]{\text{같은 크기의 각}}$을 찾아 합동인 삼각형을 찾는다.
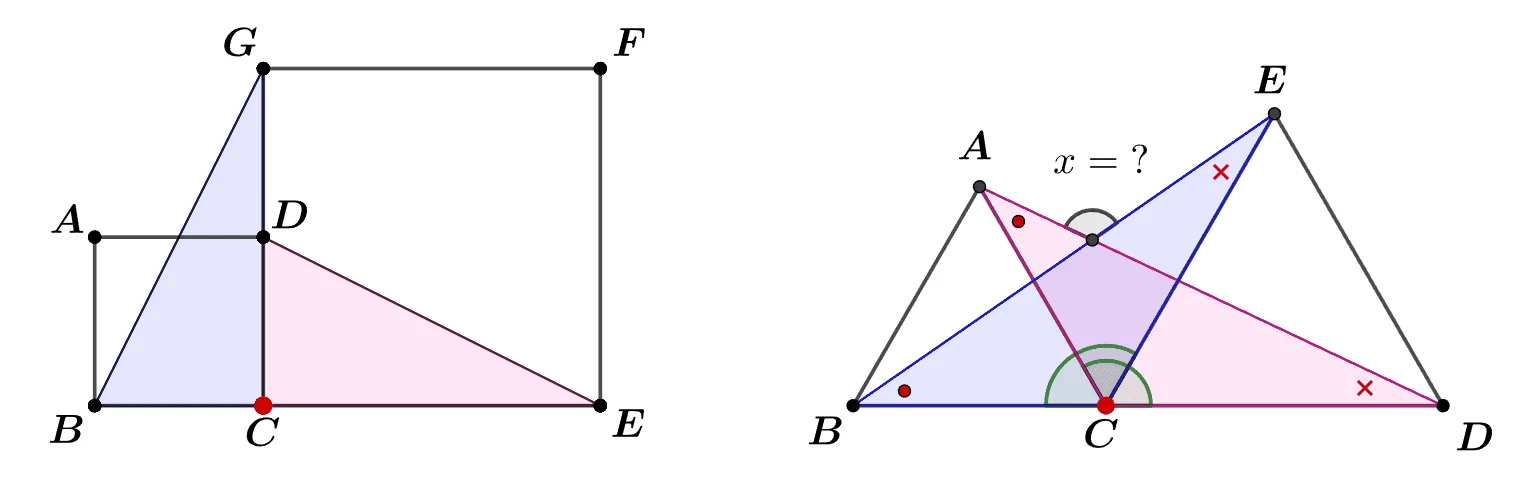
오른쪽 정삼각형에서 $x$값을 구하는 과정은 독자에게 맡기도록 하겠다.
정사각형 회전 문제
정사각형 두 개를 한 점 ${\color{red}C}$ 에 겹쳐서 회전 시키면 합동인 삼각형이 생성된다.
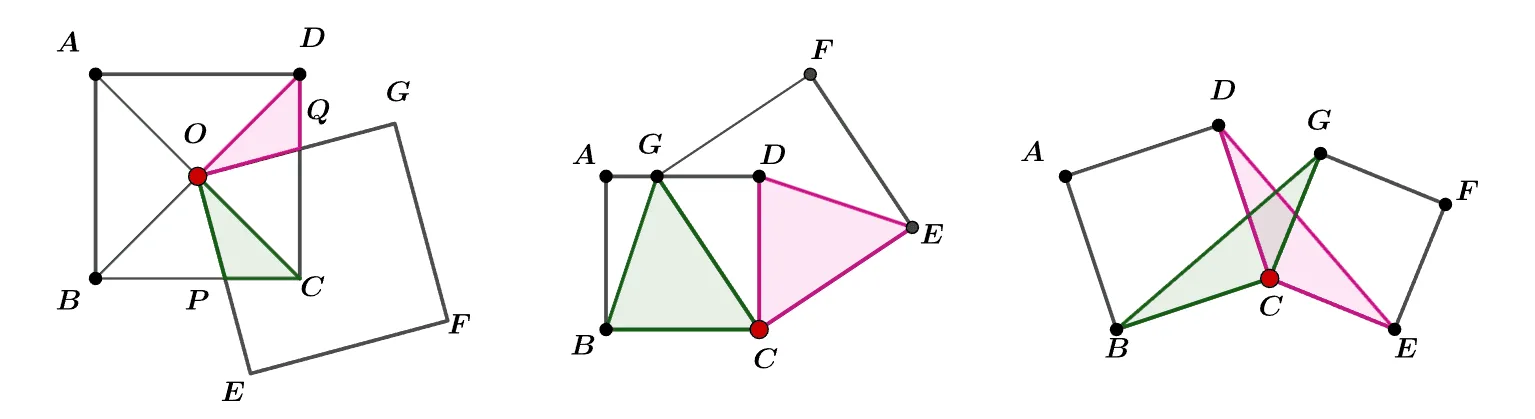
위와 같은 유형의 문제는 회전하는 중심 ${\color{red}C}$에서 같은 크기의 각을 찾으면 합동인 도형을 쉽게 구할 수 있다.
[1] $\angle{POC}=\angle{QOD}=\bbox[#ffff00]{90^\circ-\angle{COQ}}$
[2] $\angle{GCB}=\angle{ECD}=\bbox[#ffff00]{90^\circ-\angle{GCD}}$
[3] $\angle{BCG}=\angle{DCE}=\bbox[#ffff00]{90^\circ+\angle{DCG}}$
위의 사실을 적용하면 세 경우 모두 SAS 합동 조건을 만족함을 알 수 있다. 위의 사실을 이용해 다음 문제를 해결해 보자.
[문제] 정사각형 $\square{ABCD},\;\square{CEFG}$의 꼭짓점을 연결한 선분 $\overline{BG},\;\overline{DE}$에 대하여$\angle{DPG}=x$의 크기를 구하여라.
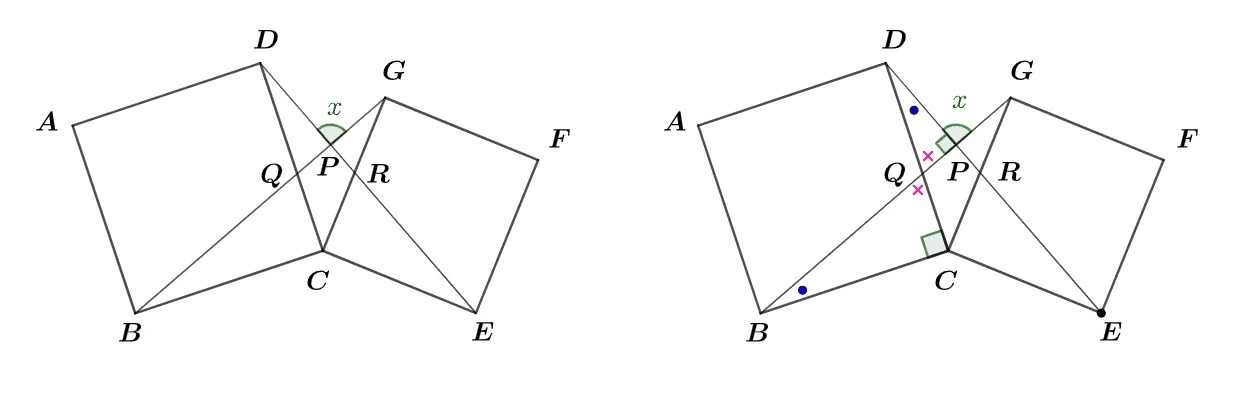
[풀이]
$\triangle{BCG}\equiv\triangle{DCE}$(SAS합동) 이므로$\angle{GBC}=\angle{EDC}={\color{blue}\bullet}$이고, 맞꼭지각으로 $\angle{BQC}=\angle{DQP}={\color{red}\times}$이다.
따라서 $x=90^\circ$이다.
정삼각형 회전 문제
정사각형과 마찬가지로 정삼각형을 한 꼭짓점 ${\color{red}C}$에 대해 회전시키면 다음과 같이 합동인 삼각형이 만들어 진다.
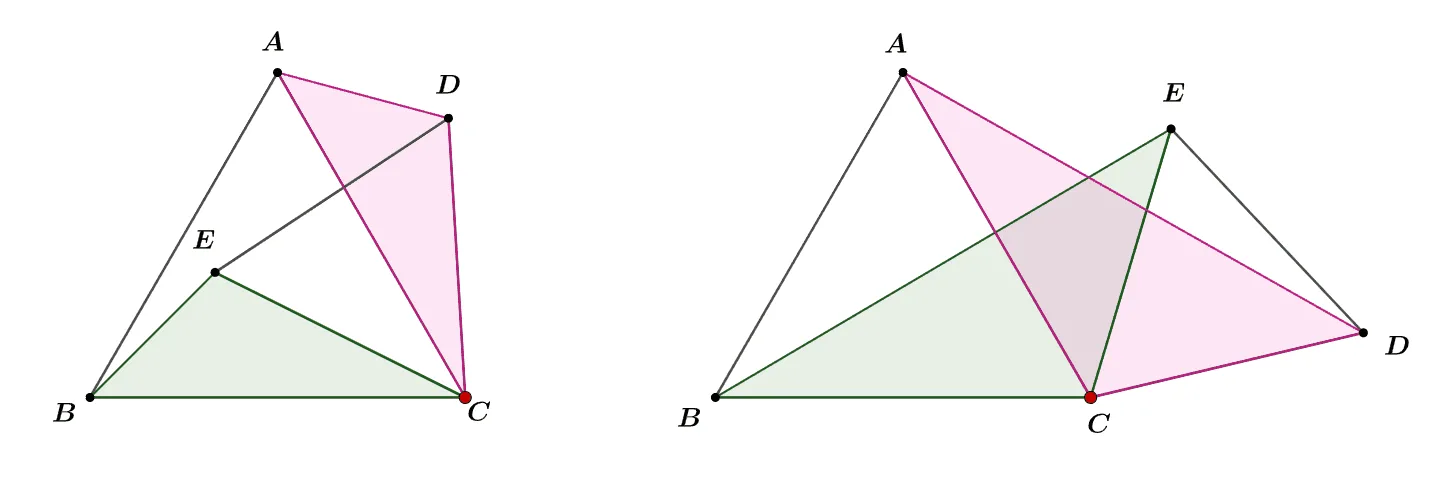
여기서도 회전하는 중심 ${\color{red}C}$에서 같은 크기의 각을 찾는 것이 핵심이다.
[1] $\angle{ECB}=\angle{DCA}=\bbox[#ffff00]{60^\circ-\angle{ACE}}$
[2] $\angle{ECB}=\angle{DCA}=\bbox[#ffff00]{60^\circ+\angle{ACE}}$
위의 사실로 부터 색칠된 두 삼각형은 SAS 합동이다.
[문제] 정삼각형 $\triangle{ABC},\;\triangle{EDC},\;\triangle{FBD}$에 대하여 다음의 물음에 답하여라.
[1]$\triangle{BDC}$와 합동인 삼각형 두 개를 찾아라.
[2]$x+y=180^\circ$임을 보여라.
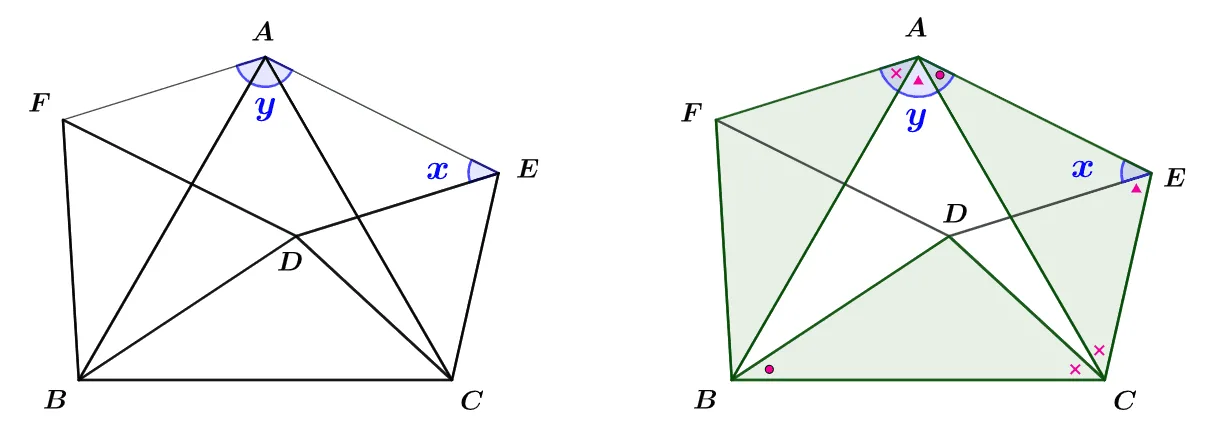
[1] 풀이
$\triangle{DCB}\equiv\triangle{ECA}$이다.
$\angle{DCB}=\angle{ECA}=\bbox[#ffff00]{60^\circ-\angle{ACB}}={\color{red}\times}$
$\overline{DC}=\overline{EC}$, $\overline{BC}=\overline{AC}$
비슷한 방법으로 $\triangle{DCB}\equiv \triangle{FAB}$이고 따라서 다음이 성립한다.
$\triangle{DCB}\equiv\triangle{ECA}\equiv \triangle{FAB}$
[2] 풀이
$\triangle{DCB} \equiv \triangle{ECA}\equiv \triangle{FAB}$이므로
$\angle{DCB}=\angle{ECA}=\angle{FAB}={\color{red}\times}$이다.
$\angle{CAE}={\color{red}\bullet}$, $\angle{CAD}={\color{red}\blacktriangle}$이라 할 때
$\triangle{CAE}$에 대하여 ${\color{red}\bullet}+{\color{red}\times}+{\color{red}\blacktriangle}+x=180^\circ$이고 $y={\color{red}\bullet}+{\color{red}\times}+{\color{red}\blacktriangle}$이다.
$\therefore\; x+y=180^\circ$
[추가 정리]
$x+y=180^\circ$이면 동위각이 같고, 따라서 $\overline{FA}\pa\overline{DE},\;\overline{FD}\pa\overline{AD}$이다.
따라서 $\square{AFDE}$는 평행사변형이다.
맺음말
이번 정리에서는 작도와 삼각형의 합동조건을 중심으로 평행선 작도, 삼각형의 결정조건, 세 변의 길이 조건, 합동조건, 대칭과 회전이동을 이용한 합동 문제 등을 다루었습니다. 대칭성과 회전을 이해하면 합동 문제 해결에 도움이 됩니다. 학습한 내용을 다양한 예제를 통해 이를 적용해 보길 바랍니다.
