입체도형의 겉넓이와 부피 문제

이번 시간에는 기둥, 뿔, 뿔대, 구를 중심으로 입체도형의 겉넓이와 부피에 대한 문제를 풀어보도록 하겠습니다.

기둥의 겉넓이와 부피

기둥의 겉넓이($S_\text{기둥}$)와 부피($V_\text{기둥}$)는 다음과 같다.

1. $S_\text{기둥}=(\text{밑넓이})\times 2+(\text{옆넓이})$
   • $(\text{옆넓이})=(\textcolor{red}{\text{밑면의 둘레}})\times (\text{높이})$
2. $V_\text{기둥}=(\text{밑넓이})\times (\text{높이})$

각기둥의 겉넓이와 부피 문제

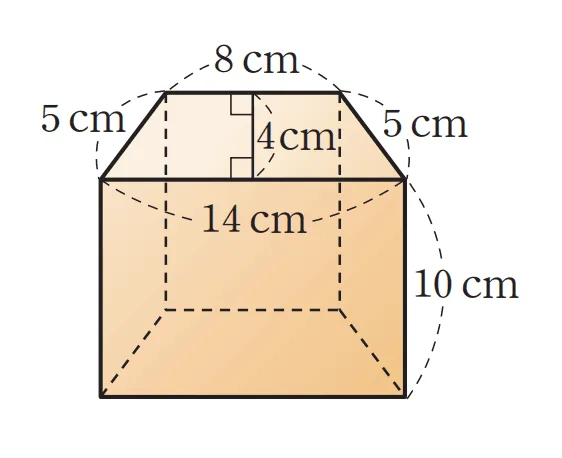
1. 주어진 사각기둥의 겉넓이와 부피를 구하여라.
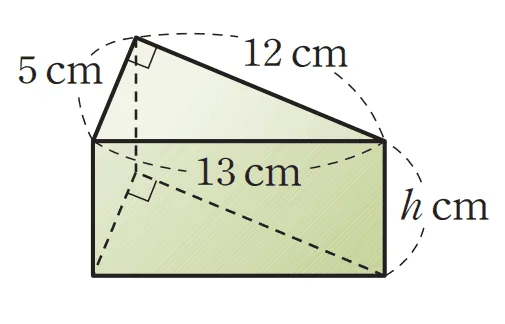
2. 밑면이 직각 삼각형이고 높이가 $h$인 삼각기둥의 겉넓이가 $195cm^2$일 때 주어진 삼각 기둥의 부피를 구하여라.

[1번 풀이]

$S_\text{기둥}=(\bbox[#ffff00]{\text{밑넓이}})\times2+(\bbox[#dcff8c]{\text{옆넓이}})$ 이고,

\begin{flalign}
\bbox[#ffff00]{\text{밑넓이}}&=\dfrac{1}{2}\times(8+14)\times 4\\[1em]
&=44(cm^2)\\[1em]
\bbox[#dcff8c]{\text{옆넓이}}&=(\textcolor{red}{\text{밑면의 둘레}})\times (\text{높이})\\[1em]
&=(\textcolor{red}{8+5+14+5})\times10\\[1em]
&=320(cm^2)
&&\end{flalign}

\begin{flalign}
S_\text{기둥}&=(\bbox[#ffff00]{\text{밑넓이}})\times2+(\bbox[#dcff8c]{\text{옆넓이}})\\[1em]
&=\bbox[#ffff00]{44(cm^2)}\times2+\bbox[#dcff8c]{320(cm^2)}\\[1em]
&=408(cm^2)
&&\end{flalign}

\begin{flalign}
V_\text{기둥}&=(\bbox[#ffff00]{\text{밑넓이}})\times (\text{높이})\\[1em]
&=\bbox[#ffff00]{44(cm^2)}\times10\\[1em]
&=440(cm^3)
&&\end{flalign}

[2번 풀이]

$S_\text{기둥}=(\bbox[#ffff00]{\text{밑넓이}})\times 2 + (\text{옆넓이})$ 이므로

$\bbox[#ffff00]{\dfrac{1}{2}\times5\times 12}\times2+(\textcolor{red}{5+12+13}) \times h =195$ 이다.

따라서 $60+30h=195$이고 일차 방정식을 풀면 $h=\dfrac{9}{2}(cm)$이다.

\begin{flalign}
V_\text{기둥}&=(\bbox[#ffff00]{\text{밑넓이}})\times (\text{높이})\\[1em]
&=\bbox[#ffff00]{\dfrac{1}{2}\times5\times 12}\times\dfrac{9}{2}\\[1em]
\therefore\; V_\text{기둥}&=135(cm^3)
&&\end{flalign}

원기둥의 겉넓이와 부피 문제

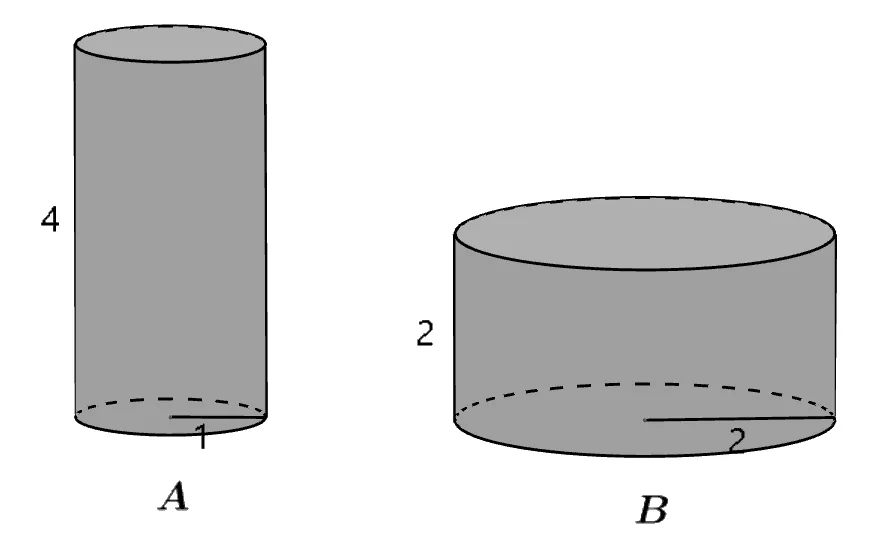
[문제] 밑면의 반지름의 길이가 $1cm$ 이고 높이가 $4cm$인 원기둥 $A$와 밑면의 반지름이 $2$배 높이는 $\dfrac{1}{2}$인 원기둥 B에 대하여 다음 물음에 답하여라.

1. 두 원기둥의 엎넓이의 크기를 비교하여라.
2. 두 원기둥의 부피를 비교하여라.

[1번 풀이]

$S_\text{기둥}=(\textcolor{red}{\text{밑면의 둘레}})\times (\text{높이})$이고 각 원기둥의 옆넓이를 $S_A,\; S_B$라고 할 때

$S_A=\textcolor{red}{2\pi}\times 4=8\pi(cm^2)$
$S_B=\textcolor{red}{4\pi}\times 2=8\pi(cm^2)$

$\therefore\; S_A=S_B$

[2번 풀이]

$V_\text{기둥}=(\bbox[#ffff00]{\text{밑넓이}})\times (\text{높이})$이고 각 원기둥의 부피를 $V_A,\;V_B$라고 할 때

$V_A=\bbox[#ffff00]{\pi}\times 4=4\pi(cm^3)$
$V_B=\bbox[#ffff00]{4\pi}\times 2=8\pi(cm^3)$

따라서 $V_B>V_A$임을 알 수 있다.

뿔의 겉넓이 부피

뿔의 겉넓이($S_\text{뿔}$)와 부피($V_\text{뿔}$)는 다음과 같다.

1. $S_\text{뿔}=(\text{밑넓이})+(\text{옆넓이})$
2. $V_\text{뿔}=\dfrac{1}{3}\times \bbox[#94feff]{V_\text{기둥}}$
   • $\bbox[#94feff]{V_\text{기둥}}=(\text{밑넓이})\times (\text{높이})$

각뿔의 겉넓이와 부피 문제

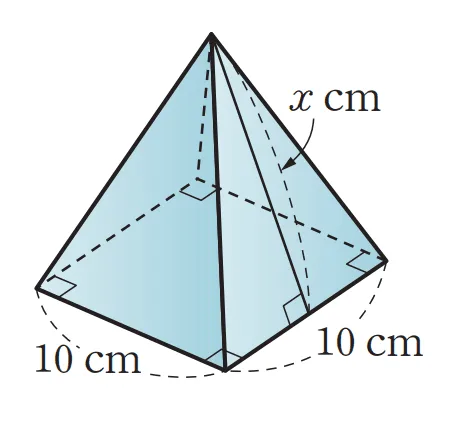
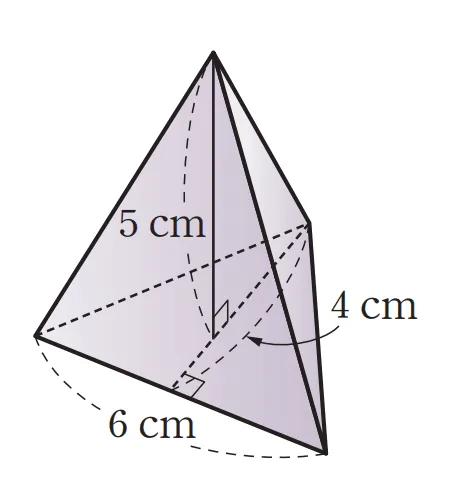
[문제] 주어진 그림에 대해 다음 물음에 답하여라.

1. 주어진 사각뿔의 겉넓이가 $360cm^2$일 때 $x$를 구하여라.
2. 주어진 삼각뿔의 부피를 구하여라.

[1번 풀이]

$S_\text{뿔}=(\bbox[#ffff00]{\text{밑넓이}})+(\bbox[#dcff8c]{\text{옆넓이}})$이므로

$S_\text{뿔}=(\bbox[#ffff00]{10\times10})+(\bbox[#dcff8c]{\dfrac{1}{2}\times 10 \times x \times 4})=360$

$\therefore \; x=13(cm)$

[2번 풀이]

$V_\text{뿔}=\dfrac{1}{3}\times(\bbox[#94feff]{V_\text{기둥}})$이므로

$V_\text{뿔}=\dfrac{1}{3}\times(\bbox[#94feff]{\textcolor{red}{\dfrac{1}{2} \times6 \times4} \times5})$

$\therefore\; V_\text{뿔}=20(cm^3)$

원뿔의 겉넓이와 부피 문제

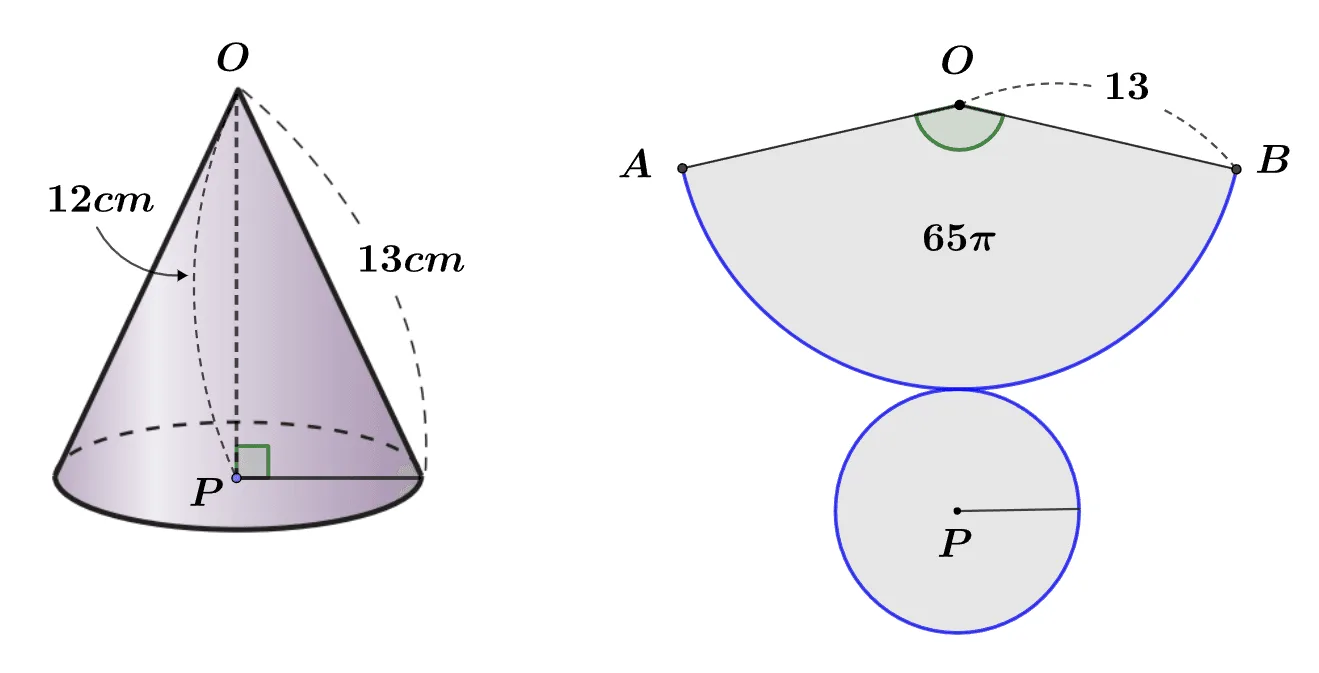
[문제] 모선의 길이와 높이가 각 각 $13cm, \;12cm$인 원뿔의 옆넓이가 $65\pi(cm^2)$ 일 때 원뿔의 부피를 구하여라.

$\text{옆넓이}=13\times\dfrac{\overset{\mmlToken{mo}{⏜}}{AB}}{2}=65\pi(cm^2)$

$\overset{\mmlToken{mo}{⏜}}{AB}=10\pi$ 이므로 원 $P$의 지름이 $10(cm)$, 반지름은 $5(cm)$이다.

\begin{flalign} V_\text{뿔}&=\dfrac{1}{3}\times(\bbox[#ffff00]{\text{밑넓이}})\times (\text{높이})\\[1em]
&=\dfrac{1}{3}\times \bbox[#ffff00]{25\pi}\times 12\\[1em]
\therefore\; V_\text{뿔}&=100\pi(cm^3)
&&\end{flalign}

뿔대의 겉넓이와 부피

뿔대의 겉넓이($S_\text{뿔대}$)와 부피($V_\text{뿔대}$)는 다음과 같다.

1. $S_\text{뿔대}=(\text{밑넓이의 합})+(\text{옆넓이})$
2. $V_\text{뿔대}=V_\text{큰 뿔}-V_\text{작은 뿔}$

각뿔대의 겉넓이와 부피

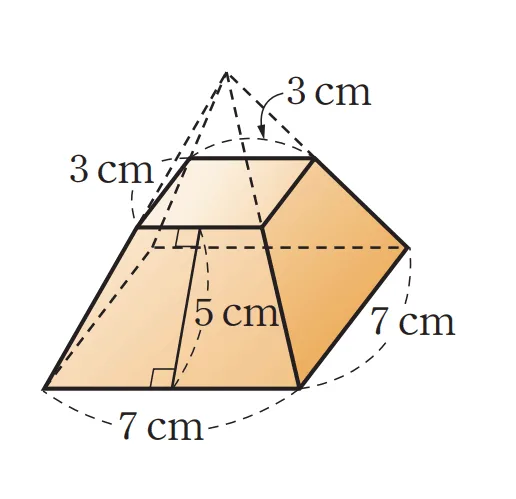
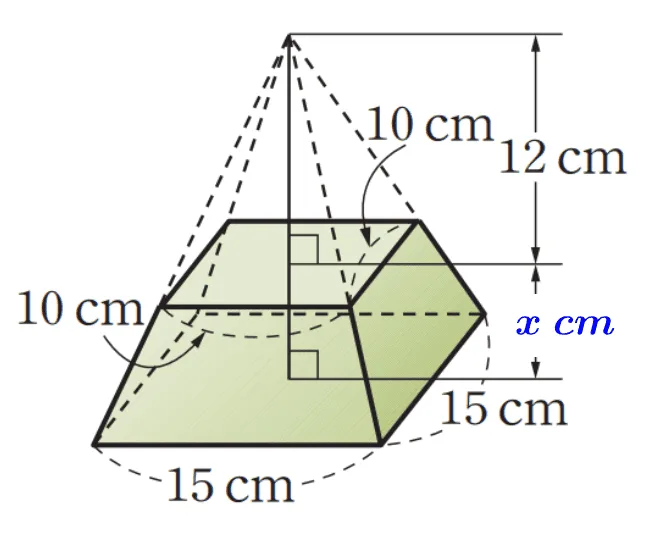
[문제] 주어진 그림에 대해 다음 물음에 답하여라.

1. 주어진 사각뿔대의 겉넓이를 구하여라.
2. 주어진 사각뿔대의 부피가 $950(cm^3)$일 때 사각뿔대의 높이를 구하여라.

[1번 풀이]

\begin{flalign}
S_\text{뿔대}&=(\bbox[#ffff00]{\text{밑넓이의 합}})+(\bbox[#dcff8c]{\text{옆넓이}})\\[1em]
&=(\bbox[#ffff00]{7^2+3^2})+(\bbox[#dcff8c]{\textcolor{red}{\dfrac{1}{2}\times(3+7)\times5}\times4})\\[1em]
\therefore\;S_\text{뿔대}&=158(cm^2)
&&\end{flalign}

[2번풀이]

\begin{flalign}
V_\text{뿔대}&=V_\text{큰 뿔}-V_\text{작은 뿔}\\[1em]
&=\dfrac{1}{3}\times15^2\times (12+x)-\dfrac{1}{3}\times 10^2 \times 12\\[1em]
&=\dfrac{1}{3}\times 5^2\{9(12+x)-48\}=950\\[1em]
\therefore\; x&=6(cm)
&&\end{flalign}

원뿔대의 겉넓이와 부피

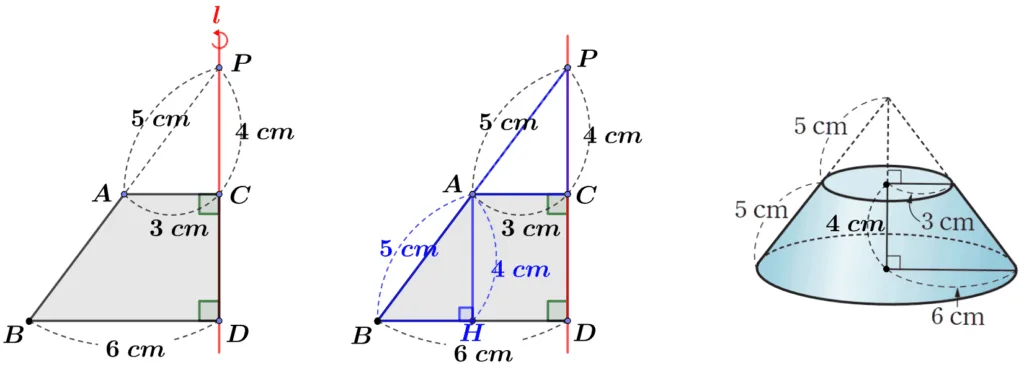
[문제] 사다리꼴 $\square{ABCD}$를 직선 $l$을 중심으로 한 바퀴 회전하여 얻은 도형의 겉넓이와 부피를 구하여라.

$A$에서 $\overline{BD}$에 내린 수선의 발 $H$에 대하여

\begin{flalign}
\triangle{PAC}&\equiv\triangle{ABH} (ASA\;\text{합동})\\[1em]
&\overline{AC}=\overline{BH}\\[1em]
&\angle{PCA}=\angle{AHB}=90^\circ\\[1em]
&\angle{PAC}=\angle{ABH}
&&\end{flalign}

$\overline{AB}=5cm$, $\overline{CD}=4cm$이다.

\begin{flalign}
S_\text{뿔대}&=(\bbox[#ffff00]{\text{밑넓이의 합}})+(\bbox[#dcff8c]{\text{옆넓이}})\\[1em]
&=(\bbox[#ffff00]{6^2\pi+3^2\pi})+\bbox[#dcff8c]{\dfrac{1}{2}(6\pi+12\pi)\times5}\\[1em]
\therefore\; S_\text{뿔대}&=90\pi(cm^2)
&&\end{flalign}

\begin{flalign}
V_\text{뿔대}&=V_\text{큰 뿔}-V_\text{작은 뿔}\\[1em]
&=\dfrac{1}{3}\times 36\pi\times8-\dfrac{1}{3}\times 9\pi\times4\\[1em]
&=\dfrac{1}{3}\times 36\pi(8-1)\\[1em]
\therefore\; V_\text{뿔대}&=84\pi(cm^3)
&&\end{flalign}

구의 겉넓이와 부피

구의 겉넓이

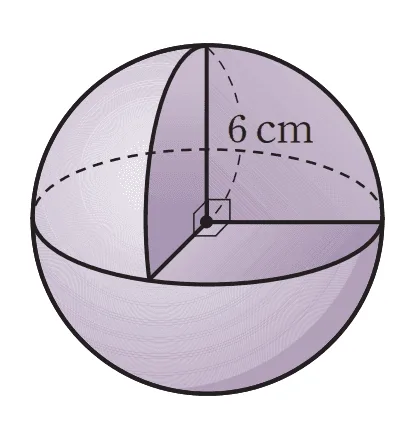
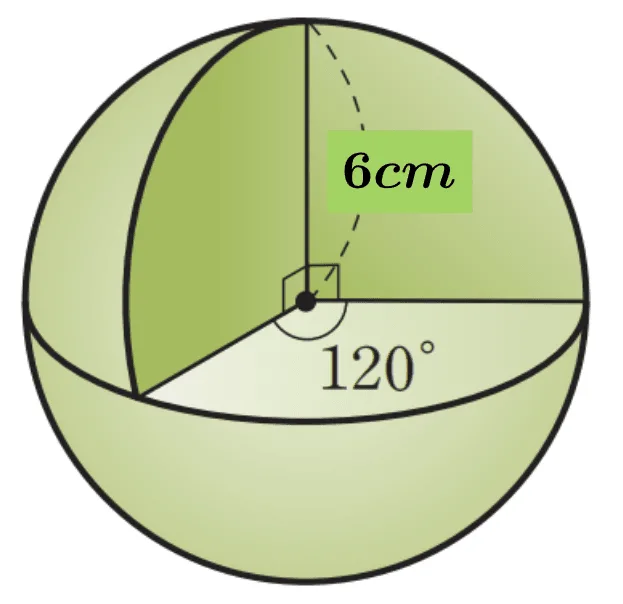
[문제] 주어진 도형에 대해 다음 물음에 답하여라.

1. 중심을 지나는 평면으로 잘라낸 반지름이 $6cm$인 구에 대하여 잘린 평면 사이의 교선이 원의 중심에서 서로$90^\circ$로 만날 때 주어진 입체도형의 겉넓이를 구하여라.
2. 중심을 지나는 평면으로 잘라낸 반지름이 $6cm$인 구에 대하여 잘린 평면 사이의 교선이 원의 중심에서 그림과 같이 $90^\circ,\; 120^\circ$로 만날 때 주어진 입체도형의 겉넓이를 구하여라.

[1번 풀이]

\begin{flalign}
S_\text{겉넓이}&=(\bbox[#ffff00]{\text{표면넓이}})+(\bbox[#dcff8c]{\text{단면넓이}})\\[1em]
&=\bbox[#ffff00]{\dfrac{7}{8}\times S_\text{구}}+\bbox[#dcff8c]{3\times S_\text{사분원}}\\[1em]
&=\bbox[#ffff00]{\dfrac{7}{8}\times 4\times 6^2 \pi}+\bbox[#dcff8c]{3\times \dfrac{1}{4}\times 6^2\pi}\\[1em]
&=\bbox[#ffff00]{126\pi}+\bbox[#dcff8c]{27\pi}=153\pi(cm^2)
&&\end{flalign}

[2번 풀이]

\begin{flalign}
S_\text{겉넓이}&=(\bbox[#ffff00]{\text{표면넓이}})+(\bbox[#dcff8c]{\text{단면넓이}})\\[1em]
&=\bbox[#ffff00]{\dfrac{5}{6}\times S_\text{구}}+\bbox[#dcff8c]{S_\text{원}\times \dfrac{300^\circ}{360^\circ}}\\[1em]
&=\bbox[#ffff00]{\dfrac{5}{6}\times 4\times 6^2 \pi}+\bbox[#dcff8c]{6^2\pi\times\dfrac{300}{360}}\\[1em]
&=\bbox[#ffff00]{120\pi}+\bbox[#dcff8c]{30\pi}=150\pi(cm^2)
&&\end{flalign}

구의 부피

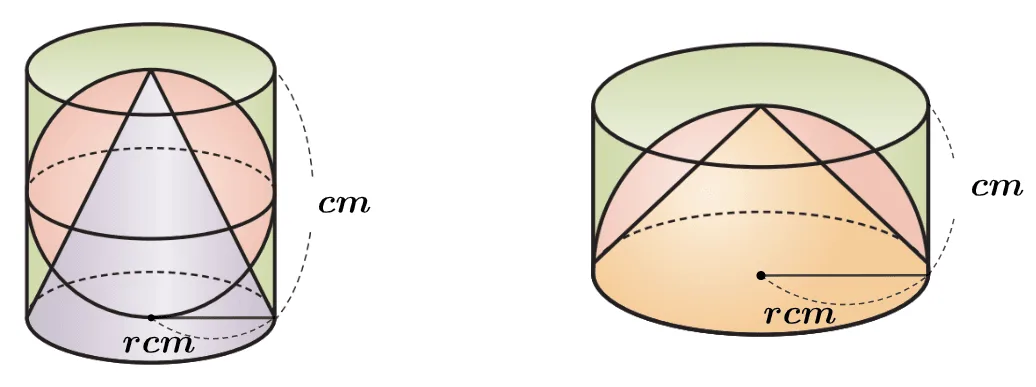
[문제] 주어진 그림에 대하여 다음의 물음에 답하여라.

1. 반지름이 $r$인 구에 딱 맞는 원기둥과 원기둥과 밑면이 합동이고 높이가 같은 원뿔에 대하여 원기둥, 원뿔, 구의 부피의 비를 구하여라.
2. 반지름이 $r$인 반구에 딱 맞는 원기둥과 원기둥과 밑면이 합동이고 높이가 같은 원뿔에 대하여 원기둥, 원뿔, 구의 부피의 비를 구하여라.

[1번 풀이]

원기둥, 원뿔, 구의 부피 : $V_\text{원기둥},\;V_\text{원뿔},\;V_\text{구}$

구의 반지름이 $r$이므로 기둥과 뿔의 밑면의 반지름이 $r$이고 높이는 $2r$이다.

\begin{flalign}
\bbox[#ffff00]{V_\text{원기둥}}&=(\text{밑넓이})\times\text{높이}\\[1em]
&=(\pi r^2)\times 2r =\bbox[#ffff00]{2\pi r^3}\\[1.5em]
V_\text{원뿔}&=\dfrac{1}{3}\times \bbox[#ffff00]{V_\text{원기둥}}\\[1em]
&=\dfrac{1}{3}\times \bbox[#ffff00]{2\pi r^3}=\dfrac{2}{3}\pi r^3\\[1.5em]
V_\text{구}&=\dfrac{4}{3}\pi r^3
&&\end{flalign}

\begin{flalign}
\therefore\; &V_\text{원기둥} : V_\text{원뿔} : V_\text{구}\\[1em]
&=2\pi r^3:\dfrac{2}{3}\pi r^3:\dfrac{4}{3}\pi r^3\\[1em]
&=1:\dfrac{1}{3}:\dfrac{2}{3}
&&\end{flalign}

[2번 풀이]

반구의 반지름이 $r$이므로 기둥과 뿔의 밑면의 반지름과 높이가 $r$이다.

\begin{flalign}
\bbox[#ffff00]{V_\text{원기둥}}&=(\text{밑넓이})\times (\text{높이})\\[1em]
&=(\pi r^2)\times r =\bbox[#ffff00]{\pi r^3}\\[1.5em]
V_\text{원뿔}&=\dfrac{1}{3}\times \bbox[#ffff00]{V_\text{원기둥}}\\[1em]
&=\dfrac{1}{3}\times \bbox[#ffff00]{\pi r^3}=\dfrac{1}{3}\pi r^3\\[1.5em]
V_\text{반구}&=\dfrac{1}{2} \times \bbox[#dcff8c]{V_\text{구}}\\[1em]
&=\dfrac{1}{2}\times \bbox[#dcff8c]{\dfrac{4}{3}\pi r^3}=\dfrac{2}{3}\pi r^3
&&\end{flalign}

\begin{flalign}
\therefore\; &V_\text{원기둥} : V_\text{원뿔} : V_\text{반구}\\[1em]
&=\pi r^3:\dfrac{1}{3}\pi r^3:\dfrac{2}{3}\pi r^3\\[1em]
&=1:\dfrac{1}{3}:\dfrac{2}{3}
&&\end{flalign}