일차함수의 그래프의 용어 (기울기, x절편, y절편)

중학교 수학에서 가장 기본이면서도 중요한 개념 중 하나는 바로 일차함수입니다. 특히 정비례 관계부터 시작해 그래프를 이해하고, 절편과 기울기의 의미를 정확히 파악하는 것은 앞으로 배우게 될 다양한 함수 개념의 기초가 됩니다. 이 글에서는 정비례 관계를 다시 복습하고, 일차함수의 그래프에서 기울기와 절편이 어떤 의미를 가지며, 어떻게 계산하는지까지 친절하게 설명하엿습니다. 이 글을 통해 일차함수가 훨씬 쉽게 느껴지시길 바랍니다.

정비례(복습)

두 변수 $x$, $y$에 대하여 다음과 같은 성질을 만족하는 관계를 ‘정비례’라고 합니다.

• 정비례 정의: $x$값이 $2$배, $3$배, $4$배, $\cdots $ 됨에 따라 $y$값도 $2$배, $3$배, $4$배 $\cdots$ 가 되는 관계

따라서 $\dfrac{y}{x}= a \text{(일정 상수)}$로 일정한 값을 가지고, 두 변수 사이의 관계를 수식으로 나타내면 다음과 같습니다.

• 정비례 관계식 일반형: $y=ax,\; (a\neq0)$

정비례 그래프 그리기

1학년에서 배운 정비례관계는 $x$값에 $y$값이 오직 하나 대응하기 때문에 $\bbox[#ffff00]{\text{함수}}$라고 할 수 있습니다. 1학년에서 배운 정비례 관계 그래프는 다음과 같이 그릴 수 있습니다.

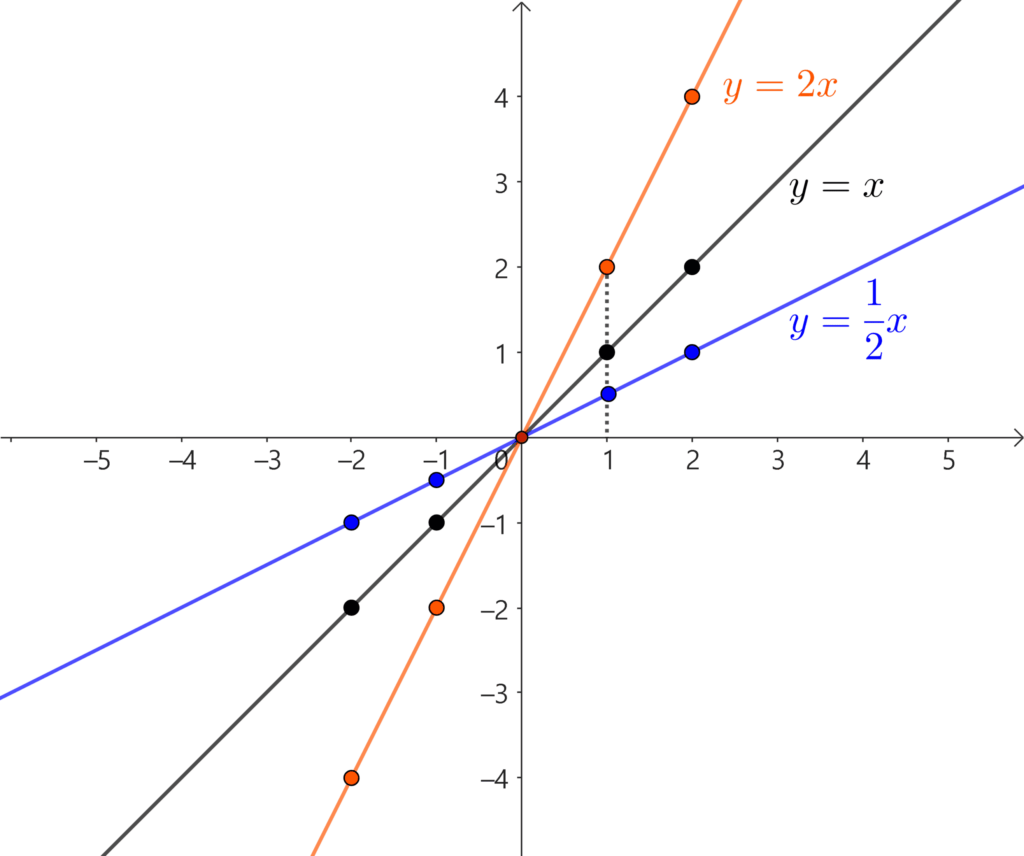
• $a>0$인 경우: $y=x,\;y=2x,\;y=3x$
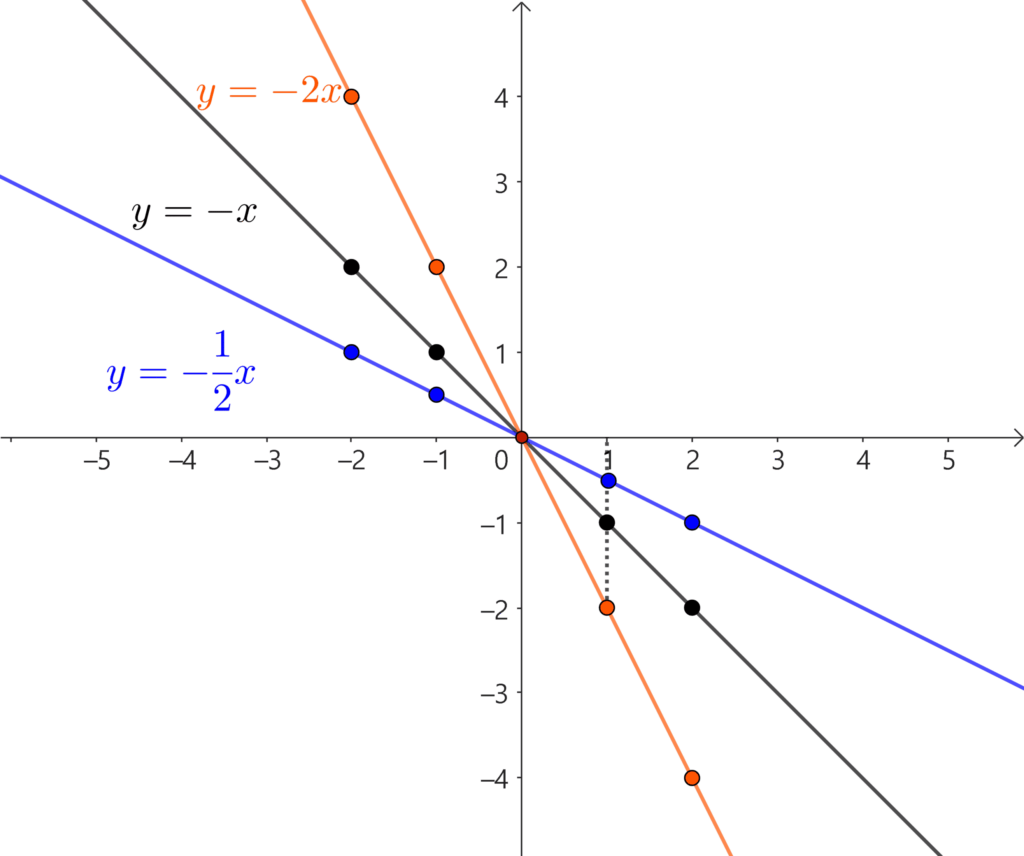
• $a<0$인 경우: $y=-x,\;y=-2x,\;y=-3x$

대응표 만들기

$a>0$: $y=x,\;y=2x,\;y=3x$

$x$	-2	-1	0	1	2
$y=x$	-2	-1	0	1	2
$y=2x$	-4	-2	0	2	4
$y=3x$	-6	-3	0	3	6

$a<0$: $y=-x,\;y=-2x,\;y=-3x$

$x$	-2	-1	0	1	2
$y=-x$	2	1	0	-1	-2
$y=-2x$	4	2	0	-2	-4
$y=-3x$	6	3	0	-3	-6

그래프 그리기

그래프 성질

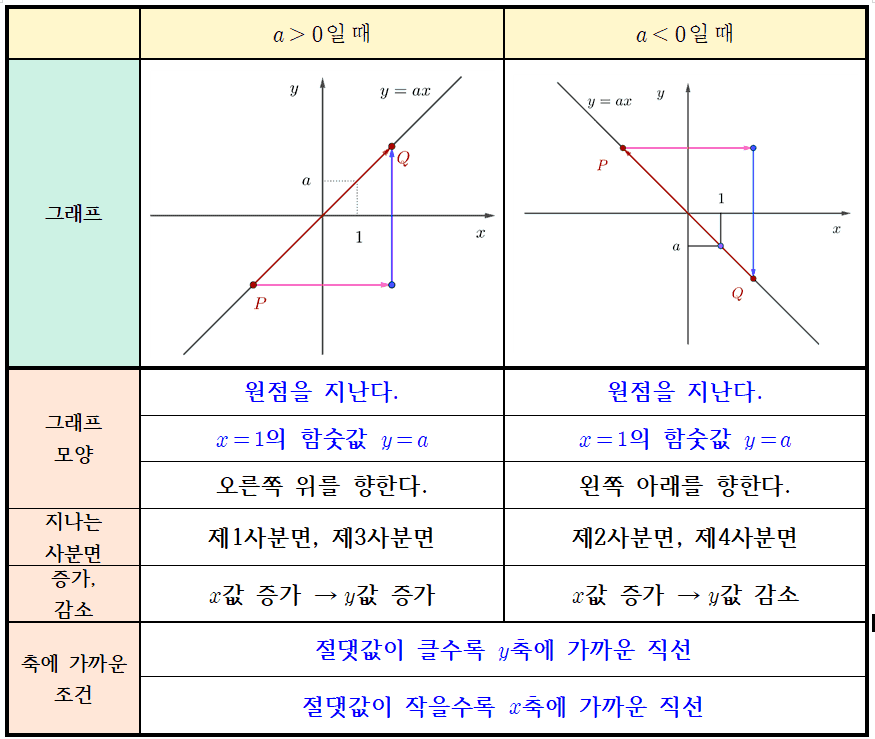
정비례 $\bbox[#ffff00]{\text{함수}}$ $y=ax,\;(a\neq0)$의 그래프 성질은 다음과 같이 정리 할 수 있습니다.

정비례에 대해 더 자세히 학습하고 싶은 학생은 아래의 글을 참고하시길 바랍니다.

• 중학교 1학년 정비례 관계식 그래프 성질

일차함수

$y$가 $x$에 대한 일차함수($f$)는 정비례를 포함하는 함수 개념으로 다음과 같이 정의 합니다.

• $y=f(x),\; f(x)=ax+b,\;(a\neq0)$
  1. $b=0$일 때: $y=ax$ 정비례 함수
  2. 예: $y=2x+3,\;y=\dfrac{x}{5}-1$

일차식과 관련된 수식

• 일차식: $ax+b,\;(a\neq0)$
• 일차방정식: $ax+b=0,\;(a\neq0)$
• 일차부등식: $ax+b<0,\;(a\neq0)$
• 일차함수: $y=ax+b,\;(a\neq0)$

일차함수 $y=ax+b$의 그래프

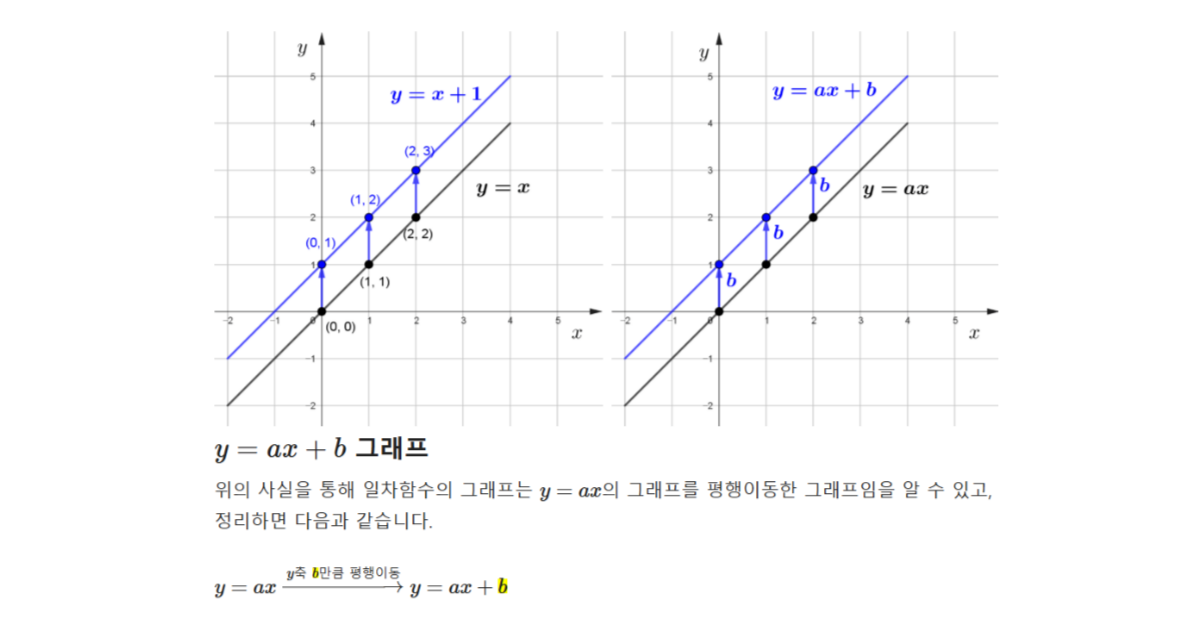
$y=x+1$와 $y=x$의 그래프를 비교해 보기 위해 먼저 대응표를 그리면 다음과 같습니다.

$x$	-2	-1	0	1	2
$y= x$	-2	-1	0	1	2
$y= x + 1$	-1	0	1	2	3

위의 대응표를 통해 $y=x+1$에서 함숫값($y$)이 1이 더 크다는 것을 알 수 있고 그래프를 그려보면 다음과 같은 결론을 내릴 수 있습니다.

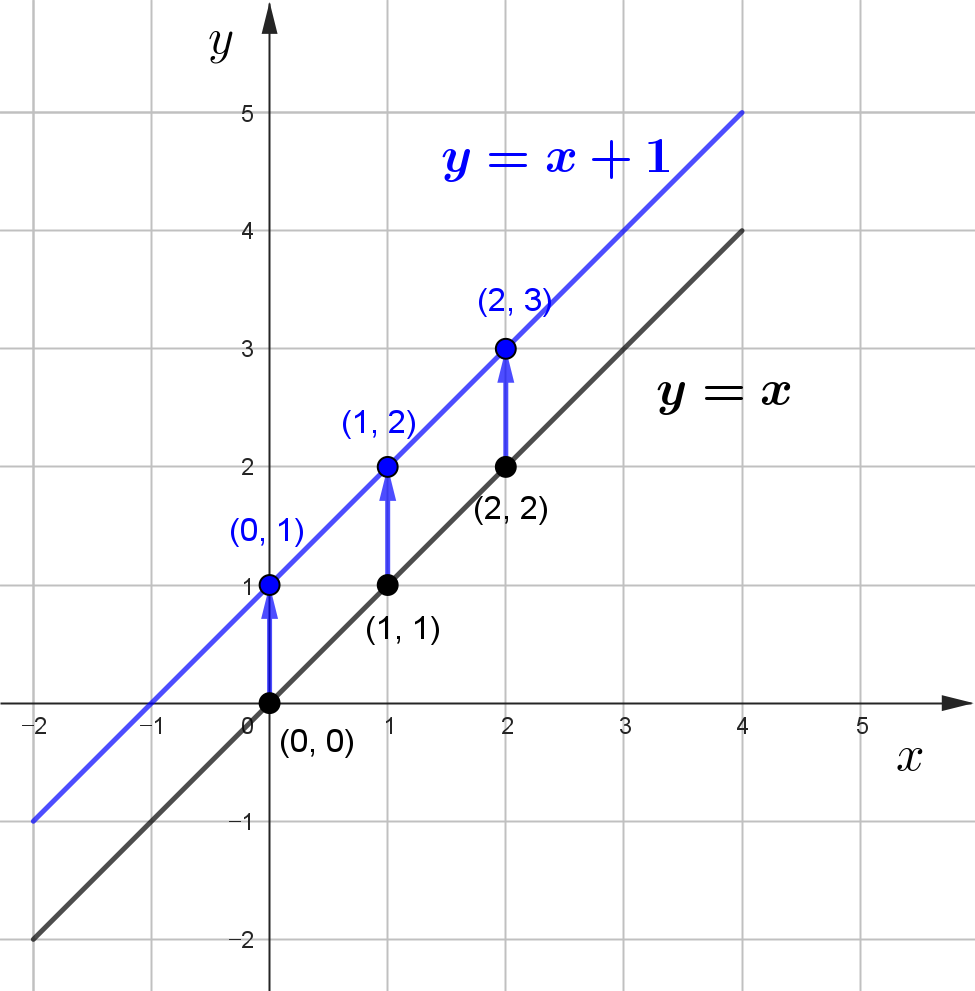
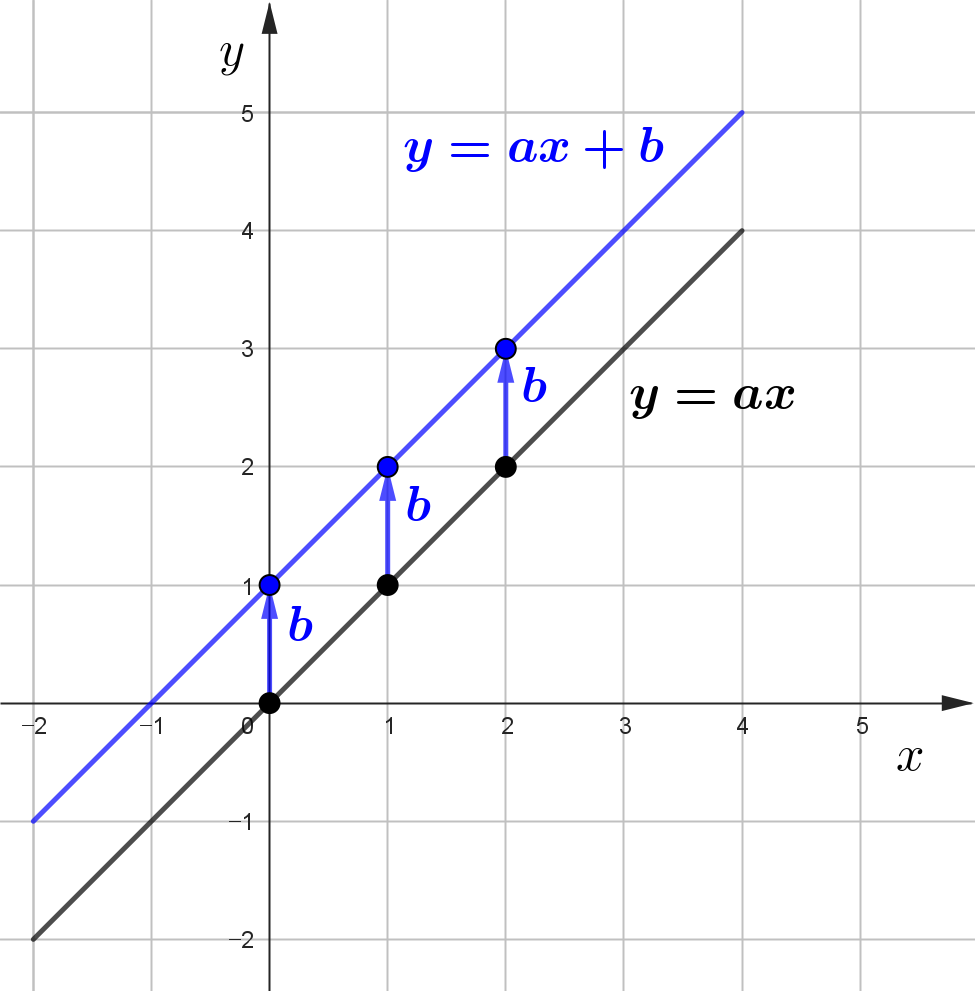
$y=ax+b$ 그래프

$y=ax+b$의 그래프는 $y=ax$의 그래프를 위쪽으로 평행이동한 그래프임을 알 수 있고, 이를 정리하면 다음과 같습니다.

• 평행이동: 한 도형을 일정한 $\bbox[#ffff00]{\text{방향}}$으로 일정한 $\bbox[#dcff8c]{\text{거리}}$만큼 옮기는 것
• $y=ax\xrightarrow[]{\bbox[#ffff00]{y}\text{축} \bbox[#dcff8c]{b} \text{만큼 평행이동}}y=ax+\bbox[#ffff00]{b}$

일차함수의 그래프 용어

위의 사실을 통해 일차함수의 그래프는 기울어진 정도가 다르고 $x$축, $y$축과 만나는 좌표에 따라 달라짐을 알수 있습니다. 이와 같은 값은 그래프의 특징을 잘 드러내기 때문에 다음과 같이 정의 하여 사용합니다.

절편

1. $x$절편: 일차함수의 그래프가 $\bbox[#ffff00]{x}$축과 만나는 점의 $\bbox[#ffff00]{x\text{좌표}}$
2. $y$절편: 일차함수의 그래프가 $\bbox[#ffff00]{y}$축과 만나는 점의 $\bbox[#ffff00]{y\text{좌표}}$

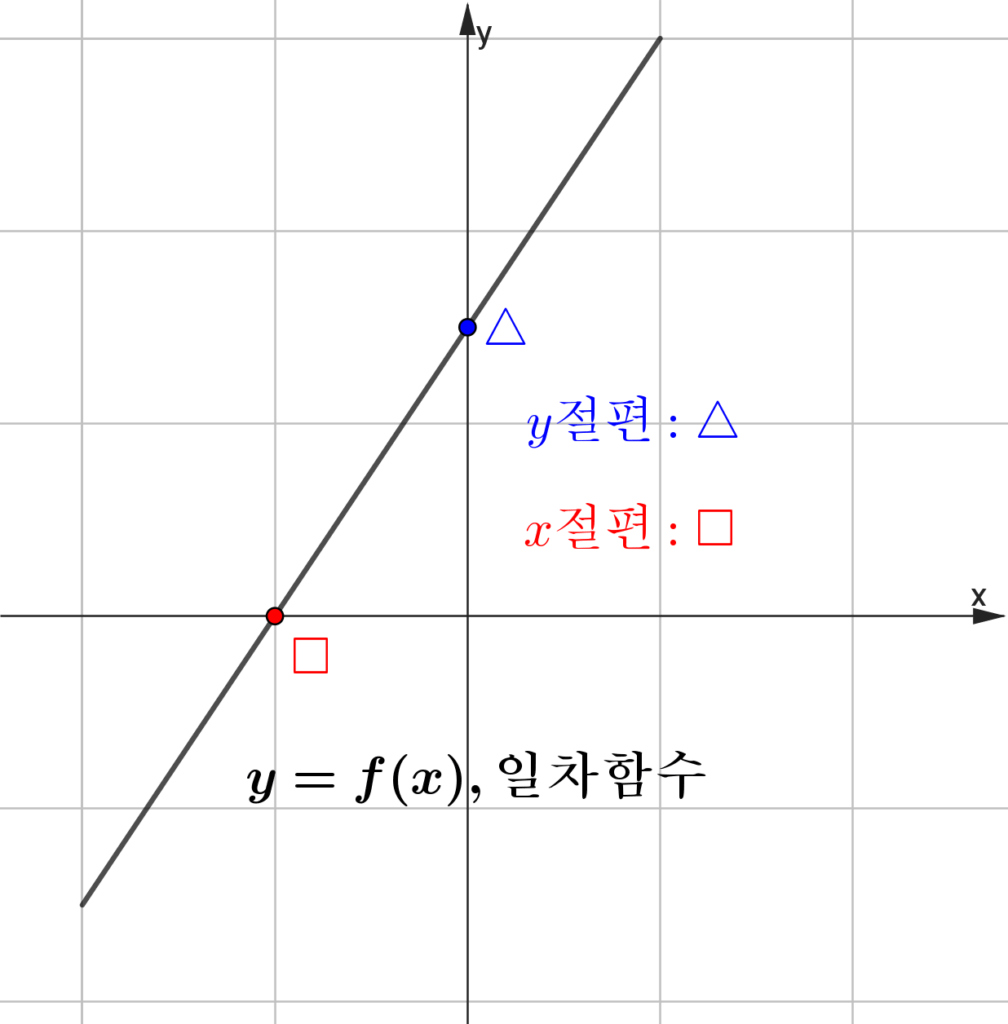
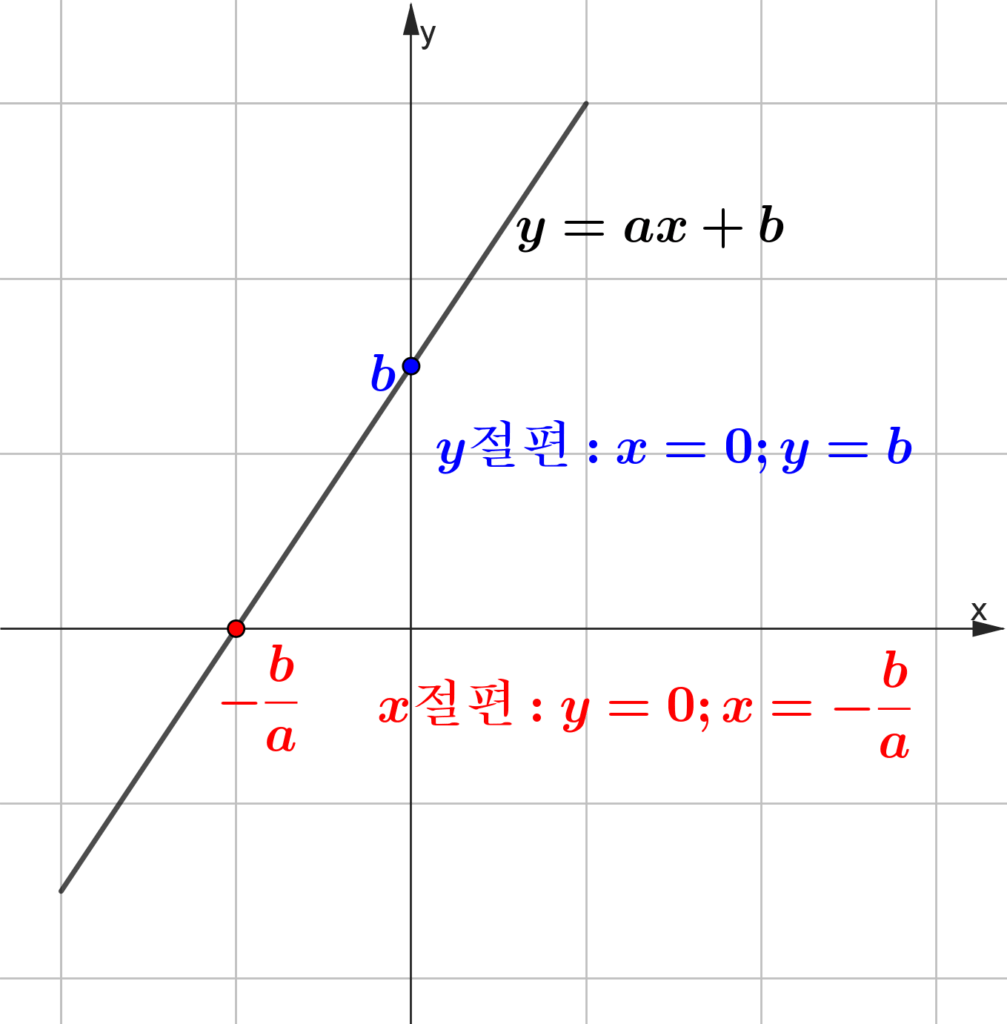
$y=ax+b,\;(a\neq0)$에 대하여 $x$절편과 $y$절편은 다음과 같이 정리할 수 있습니다.

1. $y$ 절편: $b$ ($y$축과 만나는 점의 $y$좌표)
   • 점의 $x$좌표가 $\bbox[#ffff00]{x=0}$이므로, $y$좌표 $y=a\times\bbox[#ffff00]{0}+b\rightarrow y=b$
2. $x$ 절편: $-\dfrac{b}{a}$ ($x$축과 만나는 점의 $x$좌표)
   • 점의 $y$좌표가 $\bbox[#dcff8c]{y=0}$이므로, $\bbox[#dcff8c]{0}=ax+b\rightarrow x=-\dfrac{b}{a}$

기울기

일차함수 그래프의 기울어진 정도를 기울기라고 하고 직관적으로 $x\text{값의 증가량}$에 따른 $y\text{값의 증가량}$의 비율로 정의하고 다음과 같은 사실이 성립 합니다.

1. 일차함수의 기울기: $\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}$
   • $y=\bbox[#ffff00]{a}x+b$의 기울기: $\bbox[#ffff00]{a}$

$y=2x-1$의 대응표를 이용해 기울기값을 계산해 봅시다.

$x$	$\bbox[#ffff00]{1}$	$\bbox[#dcff8c]{2}$	$\bbox[#94feff]{3}$	4	$\cdots$
$y=2x-1$	$\bbox[#ffff00]{1}$	$\bbox[#dcff8c]{3}$	$\bbox[#94feff]{5}$	7	$\cdots$

위의 결과를 통해 $x$값이 1씩 증가함에 따라 $y$값은 2씩 증가하고 있음을 알 수 있습니다. 실제로 $\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}$을 이용해 기울기를 구하면 다음과 같이 $2$로 일정함 을 알 수 있습니다.

1. $x=1\rightarrow2$ 일 때 $\dfrac{\bbox[#dcff8c]{3}-\bbox[#ffff00]{1}}{\bbox[#dcff8c]{2}-\bbox[#ffff00]{1}}=2$
2. $x=2\rightarrow3$ 일 때 $\dfrac{\bbox[#94feff]{5}-\bbox[#dcff8c]{3}}{\bbox[#94feff]{3}-\bbox[#dcff8c]{2}}=2$
3. $x=1\rightarrow3$ 일 때 $\dfrac{\bbox[#94feff]{5}-\bbox[#ffff00]{1}}{\bbox[#94feff]{3}-\bbox[#ffff00]{1}}=2$

따라서 $y=\bbox[#ffc5fd]{2}x-1$의 기울기는 $\bbox[#ffc5fd]{2}$라고 할 수 있습니다.

비슷한 방법으로 $y=ax+b$의 대응표를 이용해 기울기를 계산해 보면 다음과 같습니다.

$x$	$\bbox[#ffff00]{1}$	$\bbox[#dcff8c]{2}$	$\bbox[#94feff]{3}$	$\cdots$
$y=ax + b$	$\bbox[#ffff00]{a+b}$	$\bbox[#dcff8c]{2a+b}$	$\bbox[#94feff]{3a+b}$	$\cdots$

위의 결과를 통해 $y=ax+b$의 일차함수의 그래프는 $x$값이 1씩 증가 할 때 $y$값은 $a$만큼 증가함을 알 수 있습니다. $x=1,\;2,\;3\cdots$에서 기울기($\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}$)를 계산하면 다음과 같이 일정한 값 $a$가 됨을 알 수 있습니다.

1. $x=1\rightarrow2$ 일 때 $\dfrac{(\bbox[#dcff8c]{2a+b})-(\bbox[#ffff00]{a+b})}{\bbox[#dcff8c]{2}-\bbox[#ffff00]{1}}=a$
2. $x=2\rightarrow3$ 일 때 $\dfrac{(\bbox[#94feff]{3a+b})-(\bbox[#dcff8c]{2a+b})}{\bbox[#94feff]{3}-\bbox[#dcff8c]{2}}=a$
3. $x=1\rightarrow3$ 일 때 $\dfrac{(\bbox[#94feff]{3a+b})-(\bbox[#ffff00]{a+b})}{\bbox[#94feff]{3}-\bbox[#ffff00]{1}}=a$

따라서 일차함수 $y=\bbox[#ffff00]{a}x+b,\;(a\neq0)$의 기울기를 다음과 같이 정리할 수 있습니다.

• (기울기) $=\dfrac{y\text{값의 증가량}}{x\text{값의 증가량}}=\bbox[#ffff00]{a}(\text{일정})$