이번 시간에는 이차함수 개념을 정확히 정의하고, $y=ax^2\;(a\neq0)$인 이차함수의 그래프를 직접 그리고, 그래프의 성질을 정리하려고 한다. 더불어 이차함수의 축의 방정식과 꼭짓점에 대한 정의를 학습하고 축의 방정식과 직선의 방정식에 대한 수학적 개념을 정리해 보자.
개요
학습목표
- 함수의 개념 확장하여 이차함수 개념을 정의
- $y=ax^2 \;(a\neq0)$의 그래프를 그리기
- $y=ax^2$의 그래프 성질 정리
- 축의 방정식과 관련된 수학적 개념 정리
이차함수의 그래프는 직접 모눈종이에 그려보아야 정확한 이해에 도달 할 수 있다. 하단의 링크를 통해 학습지를 다운받아 그래프를 그려보고 내용을 정확히 정리하길 바란다.
이차함수 개념과 그래프
이차함수 개념
중학교 1, 2 학년때 배운 함수의 개념을 먼저 복습하고 이차 함수를 정리하기로 하자.
- 함수 : $x$값이 변함에 따라 $y$값이 하나씩 정해지는 대응 관계
- $x, y$는 함수 관계 기호 : $y=f(x)$
- 관계식 : $x$값이 주어질 때, $y$값을 구하는 수식
- $y=f(x)$일 때 $x=a$에서 함숫값 기호 : $f(a)$
- 이차함수 표현
1. $y=f(x),\; f(x)=ax^2+bx+c \;(a\neq0\;)$ (고등학교에서 주로 사용)
2. 이차함수 $y=ax^2+bx+c$ (중학교에서 주로 사용)
이차함수 그래프 그리기
$y=x^2$ 그래프 그리기
학습지에 이차함수의 대응관계를 표로 정리하고, 순서쌍을 구하고 좌표평면에 점을 찍어 이차함수 그래프를 그려보자.
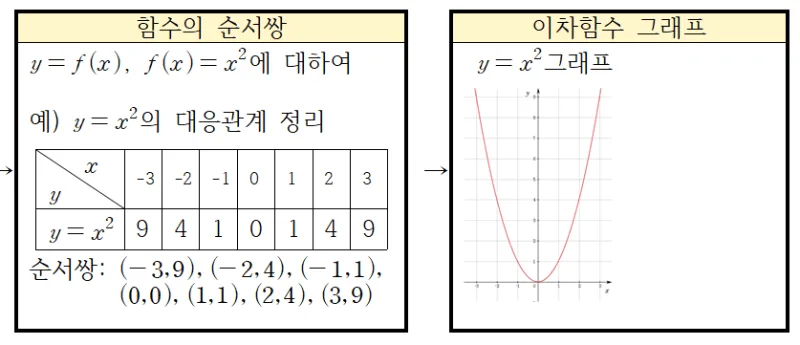
$x$의 범위를 실수로 확장하여 각 실수에 대한 순서쌍을 고려하면 무수히 많은 순서쌍 $(x,x^2)$ 점으로 찍을 수 있다. 이 점들을 모으면 아래로 볼록한 곡선이 됨을 알 수 있다. $y=x^2$의 그래프에 대하여 알아보았으니 $y=ax^2\; (a\neq0\;)$의 그래프에 대해 알아보자.
$y=ax^2$ 그래프 그리기
아래의 학습지의 빈칸을 채우고 그래프에 대한 성질을 정리해 보도록 하자.
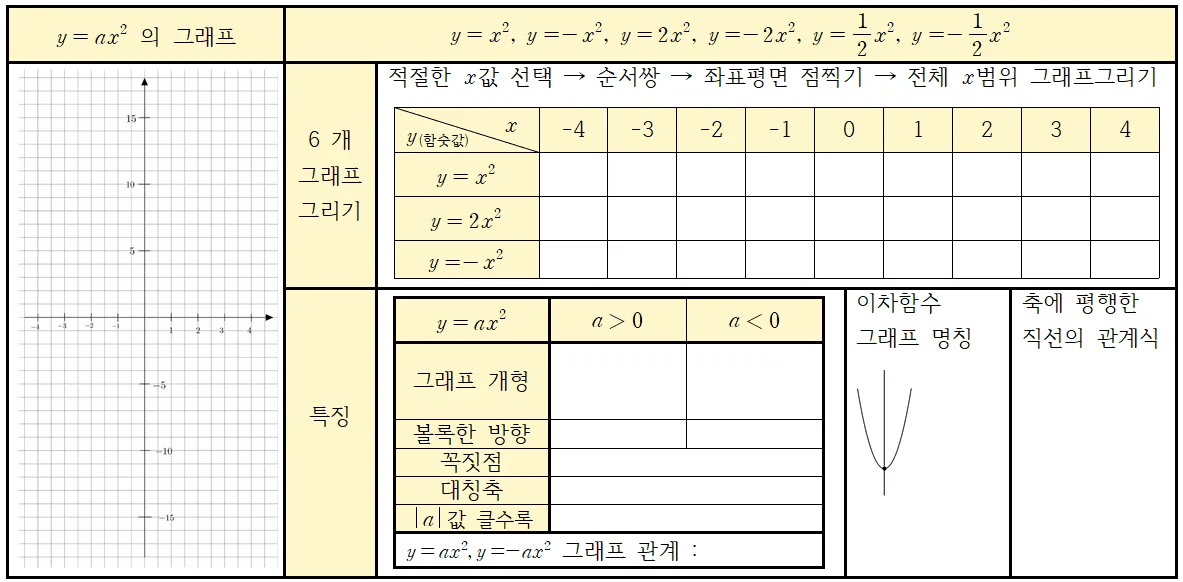
대응표를 채우기
대응표를 채우면서 함숫값 사이의 관계를 살펴보자.
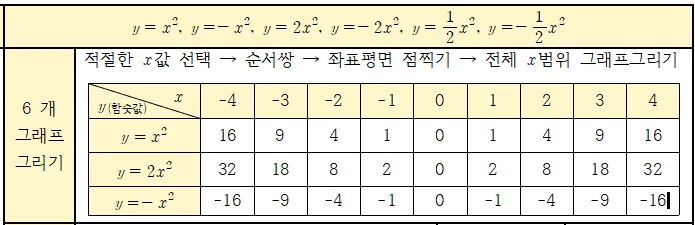
규칙
- $y=x^2$의 함숫값 : $x$ 값 $0$을 기준으로 함숫값이 대칭
- $y=2x^2$의 함숫값 : $y=x^2$의 함숫값의 $2$배
- $y=-x^2$의 함숫값: $y=x^2$의 함숫값과 부호가 반대
이차함수의 함숫값 계산
위의 규칙을 적용해 $y=\dfrac{1}{2}x^2,\; y=-2x^2,\;y=-\dfrac{1}{2}x^2$의 함숫값을 계산하면 다음과 같다.
- $y=\dfrac{1}{2}x^2$의 함숫값 : $y=x^2$의 함숫값의 $\dfrac{1}{2}$배.
- $y=-2x^2$의 함숫값 : $y=2x^2$의 함숫값과 부호가 반대.
- $y=-\dfrac{1}{2}x^2$의 함숫값 : $y=\dfrac{1}{2}x^2$의 함숫값과 부호가 반대.
그래프 그리기
위의 사실을 토대로 $y=x^2$ 의 그래프를 이용해 $y=-x^2,\;y=\dfrac{1}{2}x^2,\; y=-\dfrac{1}{2}x^2,\;y=2x^2,\;y=-2x^2$의 그래프를 그리면 아래와 같다.
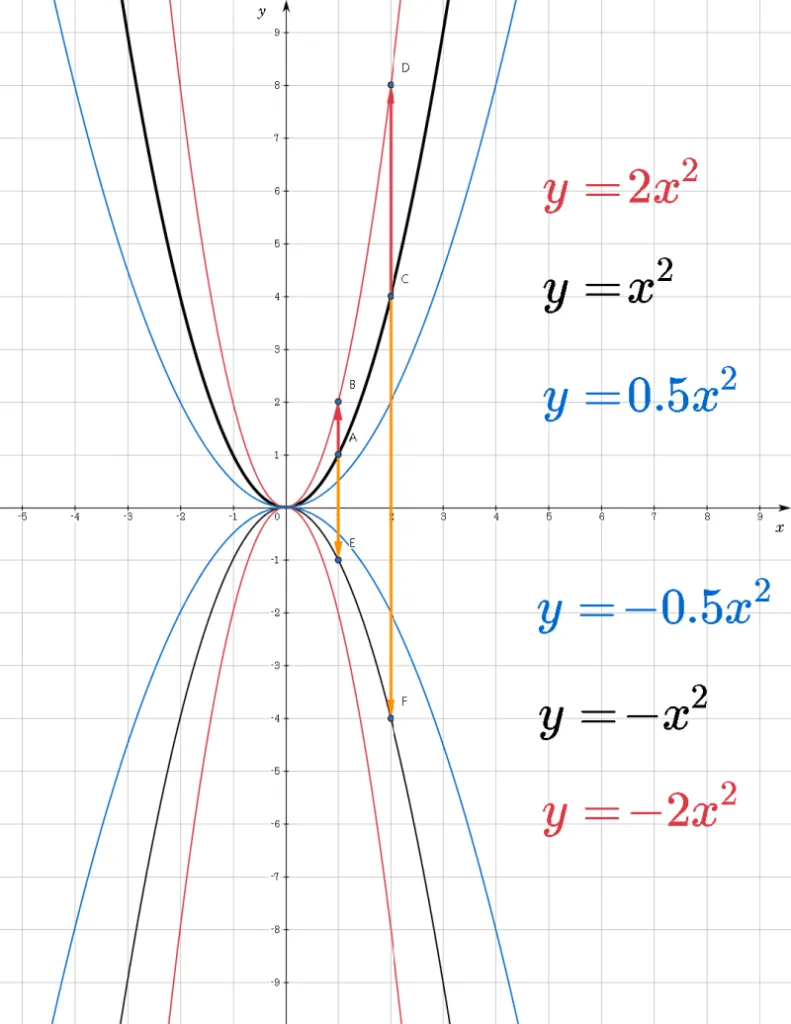
이차함수의 그래프 개형은 물체를 던질 때 나타나는 포물선과 그 모양이 같아 이차함수의 그래프를 포물선이라고 부른다.
이차함수 용어 정리
이제 이차함수 그래프와 관련된 용어에 대해 알아보기로 하자.
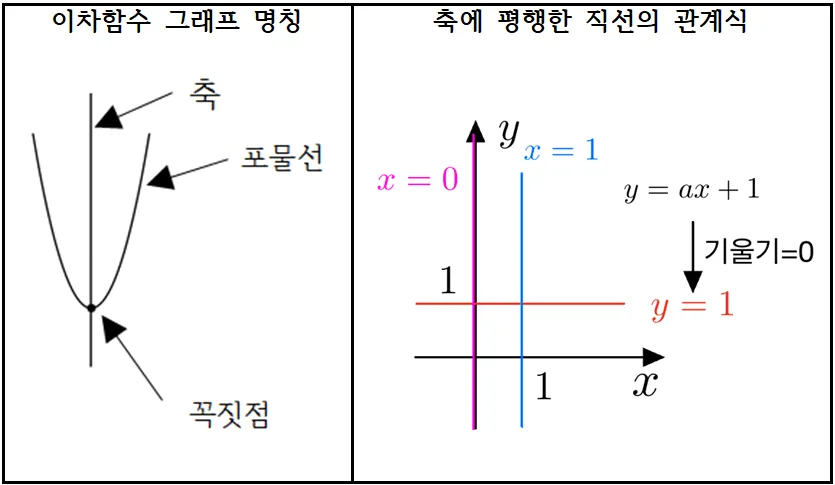
- 이차함수의 그래프 개형 : 포물선
- 축 : 이차함수의 대칭축
축의 방정식 : 축을 직선의 방정식$(x=p)$으로 표현 한 것
직선의 방정식(축의 방정식)에 대한 내용을 모르는 학생을 위해 글의 마지막에 설명을 남기도록 하겠다. - 꼭짓점 : 축과 그래프가 만나는 점
꼭짓점의 좌표 : 꼭짓점을 좌표$(p,q)$로 나타낸것
이차함수 그래프 성질
$y=ax^2\;(a\neq0)$ 그래프 기본 성질
대응표를 이용해 그린 $y=ax^2$그래프의 성질을 위의 용어를 이용해 간략히 정리하면 아래와 같다.
- 모양 : 포물선
- 축 : $y$ 축, $x=0$
- 꼭짓점 : 원점 $(0,0)$
$a$값에 따른 $y=ax^2\;(a\neq0)$ 의 그래프 성질 정리
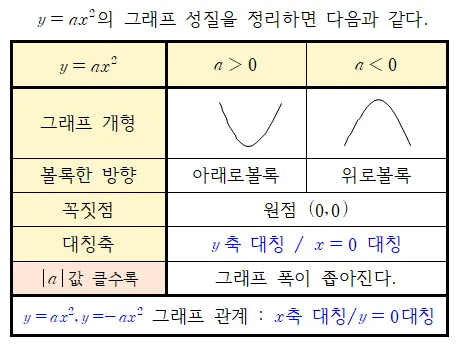
이차함수 그래프의 성질을 설명할 때 주의할 사항은 다음과 같다.
- 이차함수 그래프는 볼록한 방향으로 설명한다.
(오목한 방향으로 설명하지 않는다) - $a$의 절댓값에 커지면 그래프 폭이 좁아진다.
$a>0$; $a$값이 커지면 그래프 폭이 좁아진다.
$a<0$; $a$값이 작을수록 그래프 폭이 좁아진다.
틀리기 쉬운 문제 정리
다음의 True, False문제를 통해 개념을 확실히 정리해 보자.
[문제] $a$값이 클수록 그래프의 폭이 좁아 진다.
- [정답] False
- [해설] $a=-1,\; a=-2$인 경우를 비교하면 $-2<-1$이고 $-1$일 때 폭이 더 넓다.
- [수정] $\left|a\right|$값이 클수록 그래프 폭이 좁아진다.
[문제] $y=ax^2,\;(a\neq0)$에 대하여 다음 설명의 진위를 판별하여라
- $y=ax^2$은 $y$축 대칭이다. (True)
- $y=-ax^2$과 $y$축 대칭이다. (False)
직선의 방정식과 축의 방정식
위에서 언급한 축의 방정식이라는 용어에 대해 생각해 보기로 하자. 지금까지 그래프는 전부 함수라는 이름을 사용했는데 여기서는 축에 해당하는 직선을 함수라고 하지 않고 축의 방정식이라고 부르고 있다. 그 이유에 대해 학습해보기로 하자.이는 함수를 이해하는데 큰 도움이 되기 때문에 꼭 이해하고 넘어가길 바란다.
직선의 방정식
함수의 정의를 다시 한번 정리하고 직선의 방정식에 대해 정리해 보기로 하자.
- 함수 : $x$값에 따라 $y$값이 하나씩 대응되는 관계
- 직선의 방정식 : 좌표평면의 직선을 표현하는 관계식을 의미한다.
좌표평면에서 직선을 나타내는 그래프를 그려보면 함수인 직선도 있지만 함수가 아니 직선도 있다. 이들을 모두 직선의 방정식이라고 하고 종류별로 분류하여 나타내면 아래와 같다.- 함수인 직선의 방정식
일차함수식
상수함수식 ($x$축에 평행한 직선) - 함수가 아닌 직선의 방정식 : $y$축에 평행한 직선의 관계식
- 함수인 직선의 방정식
일차함수
$y=(일차식\;)$ 꼴로 표현된 함수
- 관계식 : $y=ax+b\;(a\neq0)$
- 기울기 : $a$
상수함수
- 상수함수 : 일차 함수의 기울기가 $a=0$일 때, $y=b$꼴의 함수
- $x$축에 평행한 직선의 관계식 : $y=(상수)$
$y$축에 평행한 직선
$x$축에 평행한 직선은 $y=(상수)$로 표현할 수 있는데 이를 확장하여 $y$축에 평행한 직선은 $x=(상수)$로 나타내기로 약속 한다. 이를 정리하면 아래와 같다.
- $y$축에 평행한 직선의 관계식 : $x=(상수)$
직선을 모두 함수라고 하지 못하는 이유
좌표평면의 직선을 함수로 표현할 수 있는 것은 아니다. 따라서 직선의 함수란 용어대신 직선의 방정식이란 용어를 사용하기로 약속 하였다. 이차함수의 축은 $y$축에 평행한 직선이므로 이 축을 나타내는 식 또한 축의 함수가 아닌 축의 방정식이라고 한다.
직선의 방정식 정의 (고등학교)
직선의 방정식에 관련된 내용은 중학교 교육과정에서는 정비례, 일차함수, 축에 평행한 직선으로 나누어 배우고, 이를 고등학교에서 통합하여 하나의 식으로 나타내는 방법으로 다시 정의 한다. 고등학교 직선의 방정식에 관련한 내용을 아래에 정리 하고 마무리 하도록 하자.
- 직선의 방정식 정의 : $ax+bx+c=0, \; (ab\neq0)$
정리
이번시간에 배운 내용을 간단히 정리하고 마무리 하도록 하자.
- 이차함수 정의 : $y=ax^2+bx+c\;(a\neq0)$
- 용어정리 : 포물선, 축(축의 방정식), 꼭짓점
- $y=ax^2 \; (a\neq0)$ 이차함수의 그래프 성질
- 직선의 방정식(중, 고등학교 개념 연결)