중학교 수학의 핵심 개념 중 하나인 원주각과 부채꼴의 호의 길이, 넓이 사이의 관계는 단순한 암기가 아니라 원리 이해가 중요합니다. 이번 글에서는 원주각의 기본 성질부터 확장 개념, 그리고 호의 길이와 부채꼴의 넓이와의 정비례 관계까지 개념을 탄탄히 정리해드립니다. 학습지 다운로드와 함께 문제를 직접 풀어보며 실력을 확실히 다져보세요.
목차
중학 수학 교재 추천
중등 1위 Mbest 강의 교재로 중학교 수학 한방에 정리하세요.
학습목표
- 원주각의 기본성질 확장
- 원주각과 호의길이, 부채꼴의 넓이 사이 관계
원주각의 성질 (복습)
원주각의 성질을 본격적으로 다루기 전에 전 시간에 증명한 성질에 대해 확인하자.
- [$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각] $=$ $\frac{1}{2}$ [$\overset{\mmlToken{mo}{⏜}}{AB}$의 중심각]
- 복습 링크 : 원주각의 뜻과 원주각과 중심각 사이의 관계
원주각의 성질 확장
위에서 확인한 원주각의 기본성질을 확장하여 정리하고 중학교 1학년에 배운 중심각과 호의 길이와 넓이 사이의 관계를 연결지어 보자.
동일한 호에 대한 원주각
원주각에 대한 기본성질에 증명과정의 내용을 추가해 확장하면 다음과 같다.
[$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각] : 일정
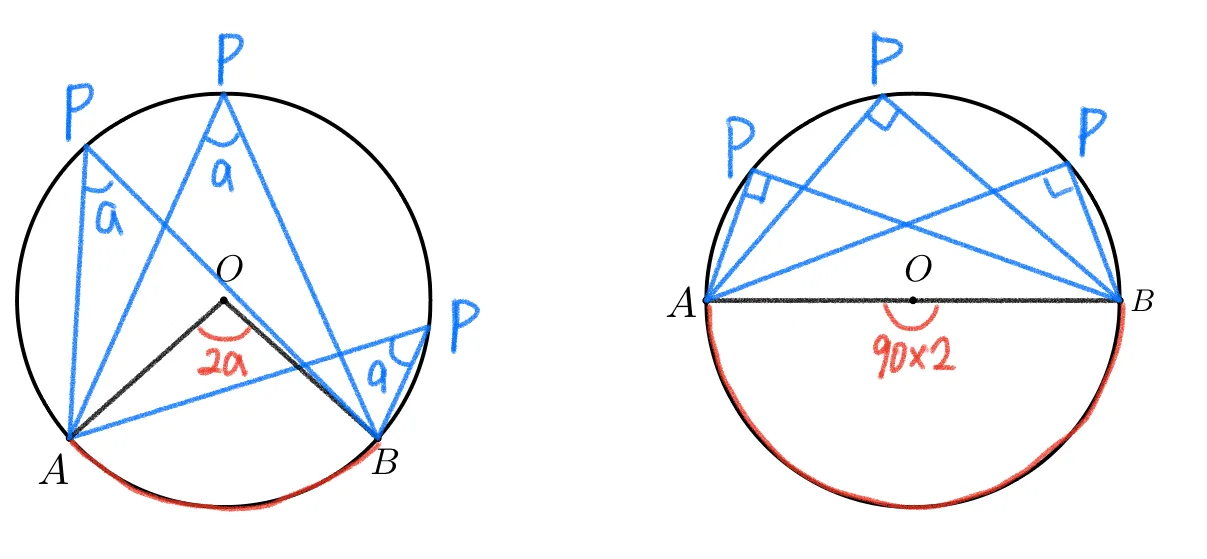
- $\overset{\mmlToken{mo}{⏜}}{AB}$의 중심각 : 유일 (일정)
- [$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각] $=$ $\frac{1}{2}$ [$\overset{\mmlToken{mo}{⏜}}{AB}$의 중심각]
- $\therefore$ $\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각 : 일정
특히 중심각이 $180^{\circ}$인 반원에 대한 원주각은 $90^{\circ}$ 이다.
한 원 또는 반지름이 같은 두 원에서 원주각
한 원 또는 반지름이 같은 두 원에 대하여 서로 다른 두 호와 두 원주각 사이에는 어떤 관계가 있는지 학습해 보자.
반지름이 같은 두 원에서 길이가 같은 호에 대한 원주각의 크기는 같다.
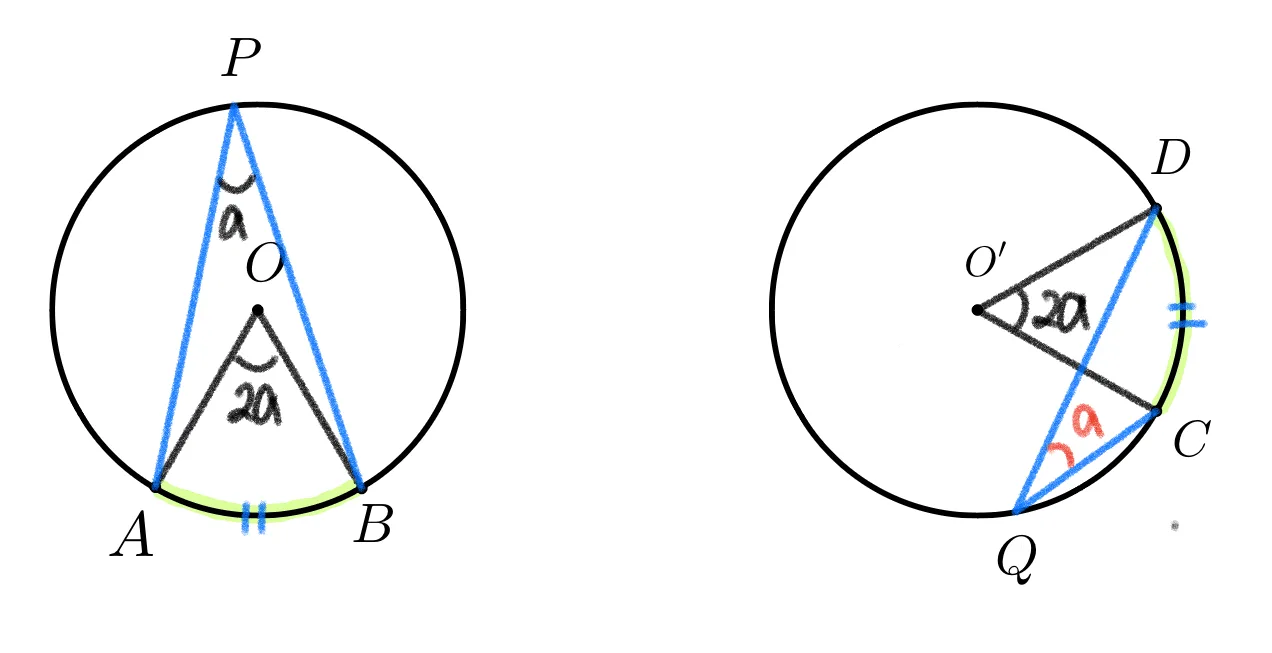
- $\overset{\mmlToken{mo}{⏜}}{AB}=\overset{\mmlToken{mo}{⏜}}{CD}$ 이면 $\angle{AOB}=\angle{CO’D}$
- $\angle{APB}=a$이면 $\angle{AOB}=\angle{DO’C}=2a$이고 $\angle{DQC}=a$이다.
- $\therefore\angle{APB}=\angle{DQC}$
한 원의 길이가 같은 호에 대해서도 비슷한 방법으로 원주각의 크기 같음을 설명할 수 있다.
- 두 호의 길이가 같으면 두 호에 대한 원주각이 같다.
- 두 호의 원주각의 크기가 같으면 두 호의 길이가 같다.
두 호의 길이가 다를 때
[$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각] $=$ $\frac{1}{2}$ [$\overset{\mmlToken{mo}{⏜}}{AB}$의 중심각]이고, 중학교 1학년때 배운 중심각과 호의길이 부채꼴 넓이관계를 정리하면 다음과 같다.
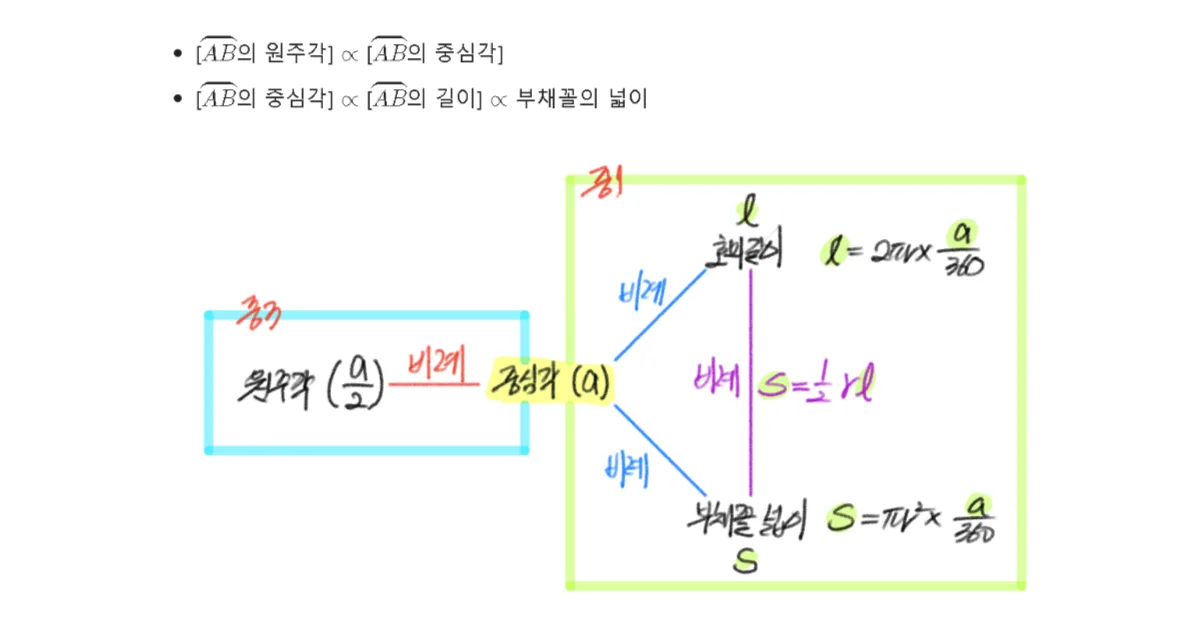
- [$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각] $\propto$ [$\overset{\mmlToken{mo}{⏜}}{AB}$의 중심각]
- [$\overset{\mmlToken{mo}{⏜}}{AB}$의 중심각] $\propto$ [$\overset{\mmlToken{mo}{⏜}}{AB}$의 길이] $\propto$ 부채꼴의 넓이
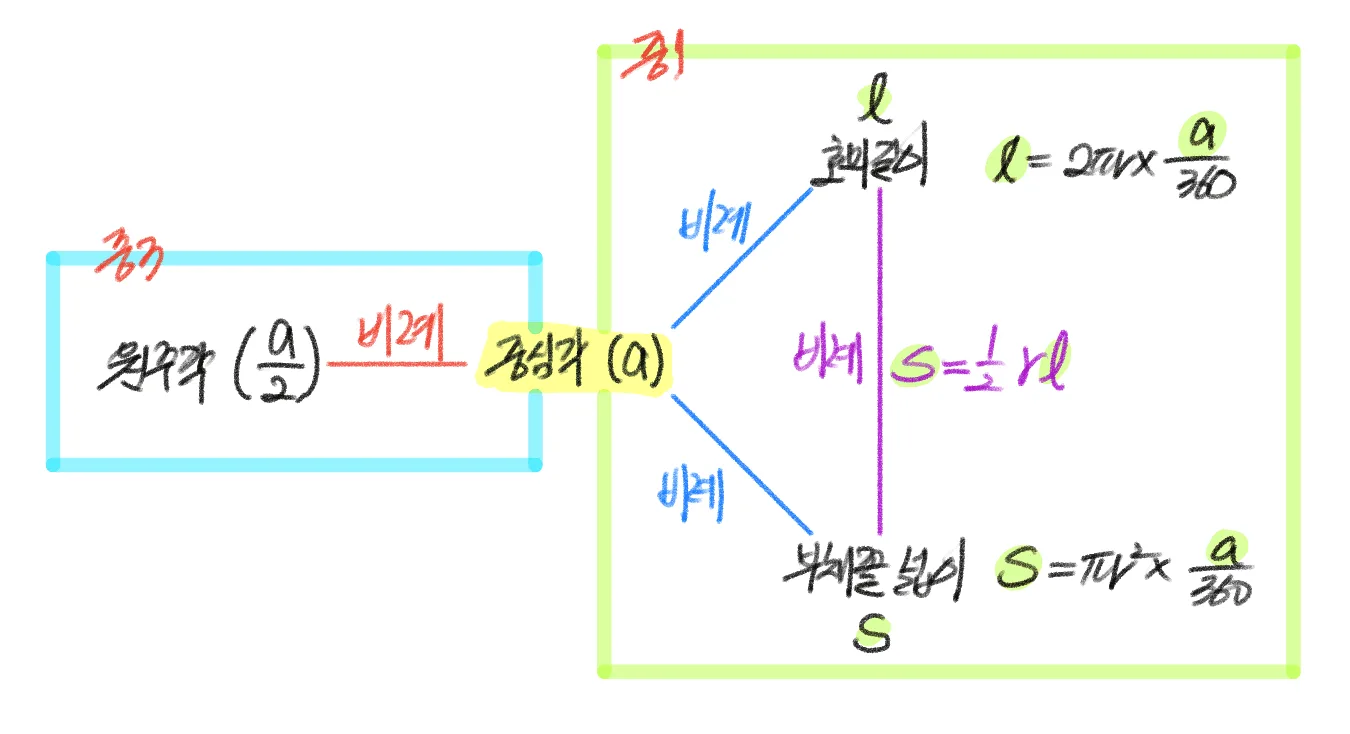
이를 원주각의 입장에서 정리하면 원주각은 중심각과 정비례하고, 호의 길이와 정비례하며, 부채꼴의 넓이와도 정비례함을 알 수 있다. 원주각과 호의 길이, 부채꼴의 넓이 사이 관계에 대한 문제를 풀어보고 학습을 마무리 하기로 하자.
원주각과 부채꼴 호의 길이, 넓이 사이 관계
다음 문제를 통해 개념을 더 정확하게 정리해 보자.
[문제] 원 $O$에서 길이가 $\pi$인 호$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각이 $15^{\circ}$이고, 부채꼴 $COD$의 넓이가 $7\pi$일 때 $\angle{CPD}$의 크기를 구하여라.
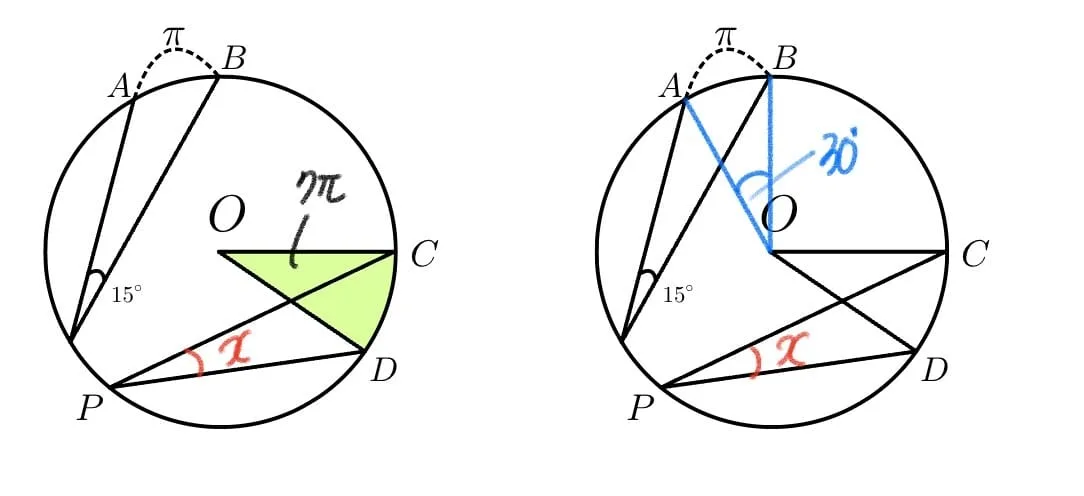
- $\overline{OA}=r$ , $\angle{AOB}=2\times15^{\circ}=30^{\circ}$ 일 때
- $\overset{\mmlToken{mo}{⏜}}{AB}=2\pi r\times\frac{30}{360}=\pi$
- $[부채꼴AOB]=\frac{1}{2}\times6\times\pi=3\pi$
- [원주각] $\propto$ [부채꼴 넓이] : $15:3\pi=x:7\pi$
- $\therefore$ $x=35^{\circ}$
정비례에 대해 배웠지만 혹시나 하는 마음에서 다시 한번 정비례에 대한 내용을 정리해 보기로 하자.
- 한 값이 2,3,4..배로 증가할 때 다른 값도 2,3,4..배로 증가하면 두 값이 정비례 관계에 있다고 한다
- 두 값이 정비례관계에 있으면 비례식을 만족한다.
정리
이번 시간에 배운 내용을 간략히 정리하고 학습을 마무리 하도록 하자. 한 원 또는 반지름이 동일한 두 원에서 다음 값들은 서로 정비례 한다. 즉 비례식을 만족한다.
- [$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각] $\propto$ [$\overset{\mmlToken{mo}{⏜}}{AB}$의 중심각] $\propto$ [$\overset{\mmlToken{mo}{⏜}}{AB}$의 길이] $\propto$ [부채꼴 $AOB $넓이]
다양한 수학 참고서, 어떻게 선택해야 할까요?
수학 실력을 키우기 위해서는 자신의 수준과 목표에 맞는 참고서를 고르는 것이 중요합니다. 연산, 개념, 유형, 심화 등 수학 참고서는 그 종류가 매우 다양하기 때문에 잘못 고르면 시간과 노력이 아까울 수 있습니다. 지금부터 수학 참고서의 종류별 특징과 선택 가이드에 대해 정리해 보겠습니다.
수학 참고서 선택 가이드
- 연산이 부족한 학생 : 연산 문제집에 집중
- 수학에 흥미를 가지고 시간을 투자할 수 있는 학생 : 개념서 1권, 유형서 1권
- 교과서 수준만 풀어 볼 학생 : 개념+유형 라이트
- 개념과 유형을 모두 마친 학생: 심화서 1권
아래에서 자신에게 맞는 참고서 종류를 확인하고 검색을 통해 빠르게 받아 학습을 이어가세요.
수학 참고서 종류
수학 참고서는 다음과 같은 연산, 개념, 유형, 개념+유형, 심화 문제집이 있습니다.
- 연산 문제집
- 센 개념연산 : 가벼운 연산 문제집
- 풍산자 반복수학 : 연산이 약한 학생을 위한 집중 훈련 교재
- 개념서
- 개념원리: 깔끔한 수학 개념서, 정리된 구조
- 숨마쿰라우데: 스토리텔링 구조, 교과서 구조
- 유형서
- 기초 유형: 베이직 센, 체크체크 베이직 N 제
- 교과서 수준: 라이트센
- 유형 반복: 센 B
- 유형+심화: 중등 RPM, 센 중등 수학
- 개념과 유형을 고르게
- 개념+유형 라이트
- 개념+유형 파워
- 심화서
- 블랙라벨, A급수학, 최상위 수학
선행 대신 심화학습 추천
개념과 유형을 충분히 익힌 학생이라면, 무리한 선행보다는 현재 학교 진도에 맞춰 심화서 한 권을 완성해보는 것이 더 효과적입니다. 그 이유는 다음과 같습니다.
- 복습: 배운 수학 개념이 연결된 심화 문제가 많음.
- 심화를 통한 선행: 심화문제를 통해 다음 학년에 배울 내용까지 자연스럽게 확장.
- 논리의 개발: 어려운 문제를 생각하는 과정에서 논리가 정돈되고 사고력이 깊어짐.
이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다.