이번 시간에는 원에내접하는 사각형의 성질에 대한 증명과 명제들을 정리해 보기로 하자. 더불어 사각형이 원에 내접할 조건에 대해 정리하고 성질과 조건 사이에 성립하는 필요충분조건에 대해 생각해 보기로 하자.
개요
학습목표
- 원주각을 응용하여 원에 내접하는 사각형에 대한 성질과 조건을 증명할 수 있다.
수학을 수학 답게 학습하기 위해서는 왜 그렇게 되는 지에 대한 확실하고 명확한 설명이 뒷받침 되어야 한다. 내접하는 사각형의 성질과 조건에 대한 정확한 증명을 제시하고 있으니 학습에 도움이 되길 바란다.
복습
원주각과 중심각사이의 관계에 대한 내용이 기억나지 않는다면 아래의 복습 링크를 학습하고 오길 바란다.
원에 내접하는 사각형의 성질
먼저 원에 내접하는 사각형의 성질에 대하여 살펴보자.
사각형 $\square{ABCD}$가 원에 내접하면 다음 성질을 만족한다.
- $\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각: $\angle{ACB}=\angle{ADB}$
- $\angle{A}+\angle{C}=\angle{B}+\angle{D}=180^{\circ}$ (대각의 크기의 합이 $180^{\circ}$)
- [한 외각의 크기] $=$ [이웃 하는 내각의 대각 크기]
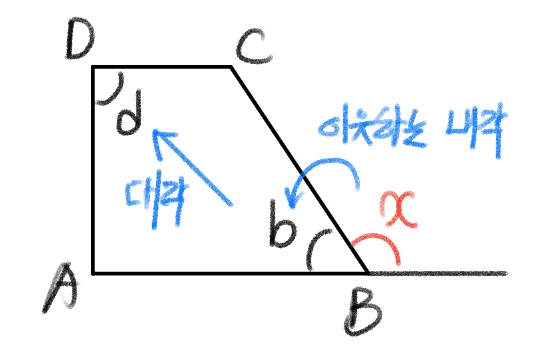
증명1
- [$\overset{\mmlToken{mo}{⏜}}{AB}$의 원주각] : $\angle{ACB}=\angle{ADB}$이 성립한다.
증명2
- [$\overset{\mmlToken{mo}{⏜}}{CBA}$의 원주각] $=d$ 이므로 [$\overset{\mmlToken{mo}{⏜}}{CBA}$ 중심각] $=2d$
- [$\overset{\mmlToken{mo}{⏜}}{CA}$의 원주각] $=b$ 이므로 [$\overset{\mmlToken{mo}{⏜}}{CBA}$ 중심각] $=2b$
- $2b+2d=360^{\circ}$이므로 $b+d=180^{\circ}$ 이다.
증명3
- $b+d=180^{\circ}$ ($\because$ 증명2), $b+x=180^{\circ}$ , 따라서 $x=d$
원에 내접하는 사각형의 성질에 대한 명제
위의 사실을 수학적인 기호로 따로 정리하면 다음과 같다.
- $\square{ABCD}$가 원에 내접 $\Rightarrow\angle{ACB}=\angle{ADB}$
- $\square{ABCD}$가 원에 내접 $\Rightarrow\angle{A}+\angle{C}=\angle{B}+\angle{D}=180^{\circ}$
- $\square{ABCD}$가 원에 내접 $\Rightarrow$ [한 외각의 크기] $=$ [이웃 하는 내각의 대각의 크기]
다음으로 위와 같은 수학적 조건을 만족하는 사각형이 원에 내접 하는지에 대해 생각해 보자.
사각형이 원에 내접할 조건(중학교 교육과정 밖)
그렇다면 화살표 오른쪽의 조건을 만족하는 네 점은 원에 내접하는 사각형을 만드는지에 대해서도 알아보기로 하자.
원의 결정조건
각 조건에 대한 증명에 앞서 원을 결정하는 최소 점의 개수에 대해 알아보자.
- 원을 결정하는 최소한의 점의 개수는 3개이다.
세 점을 동시에 지나는 원은 세 점을 꼭짓점으로 하는 삼각형의 외접원으로 결정 지을 수 있기 때문이다. 따라서 서로 다른 세 점은 한 원 위에 있고 그 원은 유일하다고 할 수 있다.
사각형이 원에 내접할 조건 3가지
일반적으로 서로 다른 네 점은 항상 한 원 위에 있는 것은 아니다. 예를 들어 직사각형이 아닌 평행사변형은 원에 내접하지 않는다. 하지만 아래의 조건을 만족하는 서로 다른 네 점은 한 원 위에 존재한다고 할 수 있다.
어느 세 점도 일직선 상에 있지 않는 서로 다른 네 점 $A,B,C,D$에 대하여 사각형 $\square{ABCD}$가 다음을 조건 중 하나를 만족하면 네 점은 한 원 위에 있다.
- $\angle{ACB}=\angle{ADB}$
- $\angle{A}+\angle{C}=\angle{B}+\angle{D}=180^{\circ}$
- [한 외각의 크기] $=$ [이웃 하는 내각의 대각의 크기]
첫 번째 조건 증명
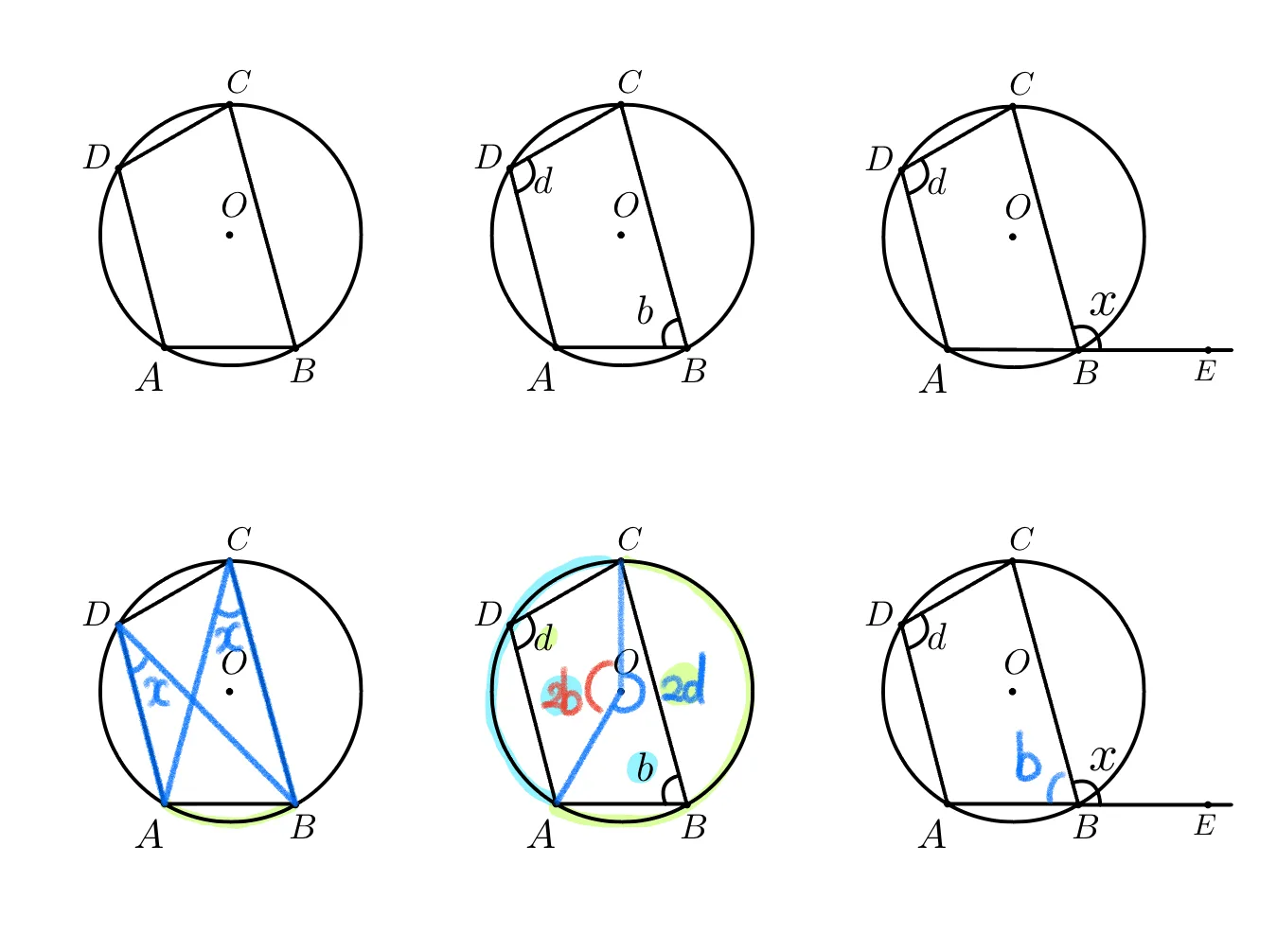
- 사각형 $\square{ABCD}$를 구성하는 네 점에 대하여 $\angle{ACB}=\angle{ADB}$ 을 만족하면 사각형은 원에 내접함을 보여라.
$\triangle{ABC}$의 외접원 : $O$에 대하여
- $\angle{ACB}=\angle{ADB}$이고 $D$가 원$O$ 외부에 있다고 한다면,
$\overline{AD}$과 원의 교점 $E$에 대해 $\angle{ACB}=\angle{AEB}=\angle{ADB}$이다.
$\angle{AEB}=\angle{ADB}$는 명백히 말도 안된다. 따라서 $D$는 원$O$의 외부에 있지 않다. - $\angle{ACB}=\angle{ADB}$이고 $D$가 원$O$ 내부에 있다 해도 말이 안된다.
직접증명이 어렵기에 귀류법으로 마무리 하였다.
두 번째 조건 증명
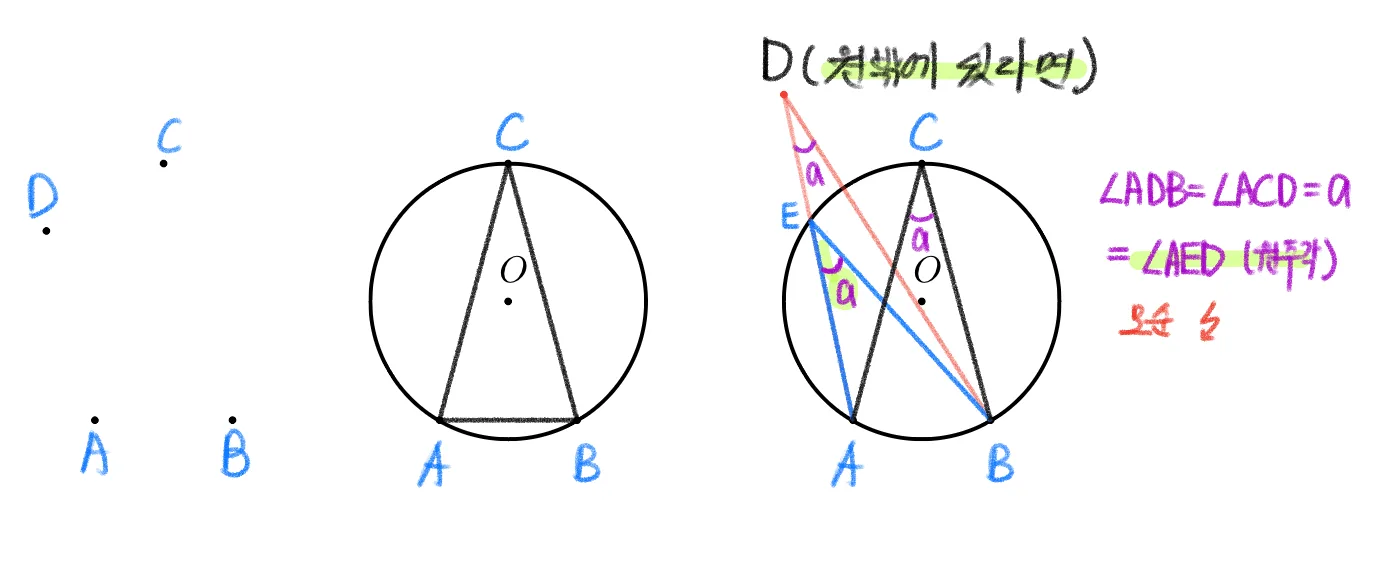
- 사각형 $\square{ABCD}$를 만드는 네 점에 대하여 $\angle{A}+\angle{C}=\angle{B}+\angle{D}=180^{\circ}$이면 사각형은 원에 내접함을 보여라.
$\triangle{ABC}$의 외접원 : $O$에 대하여
- $\angle{ABC}+\angle{ADC}=b+d=180^{\circ}$이고 $D$가 원$O$ 외부에 있다고 한다면,
$\overline{AD}$과 원의 교점 $E$에 대하여 $\angle{ABC}+\angle{AEC}=b+e=180^{\circ}$이고 $d=e$이다.
$d=e$임은 명백히 말도 안된다. 따라서 $D$가 원$O$ 외부에 있지 않다. - $\angle{ABC}+\angle{ADC}=b+d=180^{\circ}$이고 $D$가 원$O$ 내부에 있다 해도 말이 안된다.
직접 증명이 어렵기 때문에 귀류법을 사용하였다.
세 번째 조건 증명
내대각
증명을 하기 전에 내대각에 대한 용어를 먼저 정리하자.
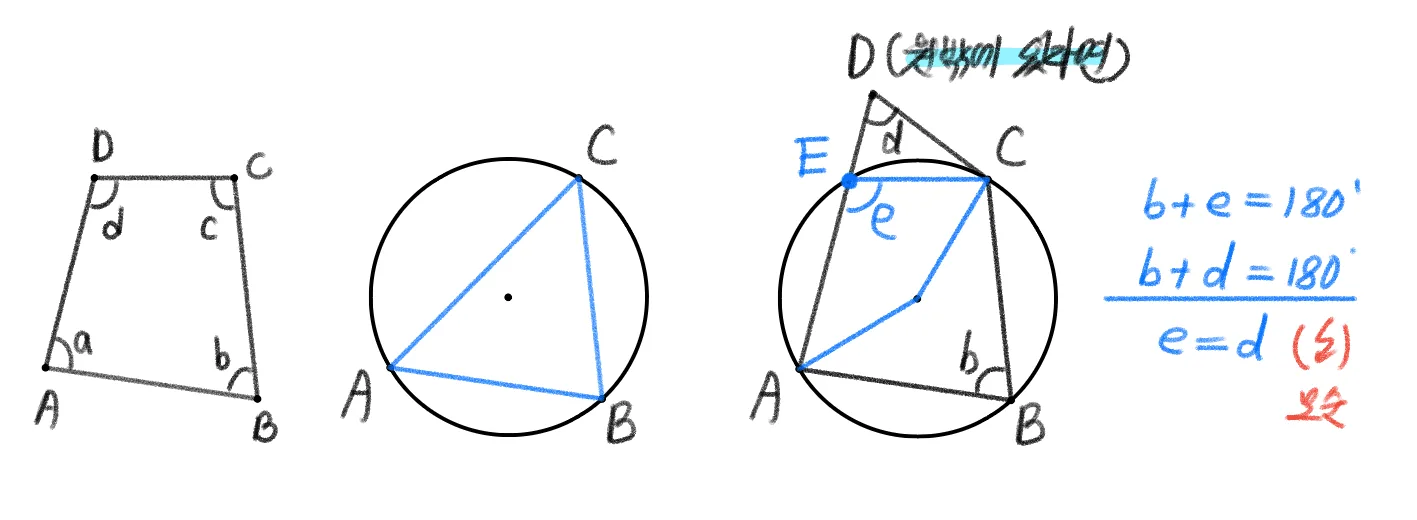
용어정의
- $x$ : $\square{ABCD}$의 외각
- $b$ : 외각 $x$와 이웃하는 내각
- $d$ : $b$의 대각
- $d$ : 외각 $x$의 내대각
일반적으로 $\angle{x}$ $\neq$ [$\angle{x}$의 내대각($\angle{d}$)] 이다.
증명
- 사각형 $\square{ABCD}$을 구성하는 네 점에 대하여 한 외각의 크기와 내대각의 크기가 같으면 사각형은 원에 내접함을 보여라.
- $[\square{ABCD}의 외각]=[외각의 내대각]$이면 $x=d$ 이고
- $x+b=d+b=180^{\circ}$이다.
- $d+b=180^{\circ}$이면 두 번째 증명에 의해 사각형은 원에 내접한다.
정리
사각형 $\square{ABCD}$를 만들 수 있는 네 점에 대하여 다음은 동치 명제이다.
- $\square{ABCD}$가 원에 내접 $\Leftrightarrow\angle{ACB}=\angle{ADB}$
- $\square{ABCD}$가 원에 내접 $\Leftrightarrow\angle{A}+\angle{C}=\angle{B}+\angle{D}=180^{\circ}$
- $\square{ABCD}$가 원에 내접 $\Leftrightarrow$ [한 외각의 크기] $=$ [내대각의 크기]