원과 부채꼴은 초등학교에서 배우지만 중학교 1학년 $\pi$ 를 이용해 개념을 다시 정리하게 됩니다. $\pi$를 이용해 원과 부채꼴 문제를 유형별로 정리 하면서 기하적 사고력을 키우는 시간이 되길 바랍니다.
개요
현과 지름에 관련된 문제
평행선 유형
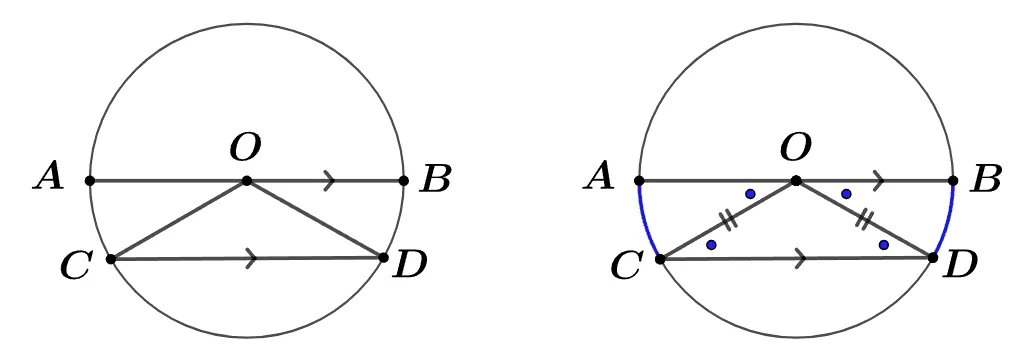
지름이 $\overline{AB}$인 원 $O$에 대하여 $\overline{AB}⫽\overline{CD}$ 일때 다음이 성립한다.
$\angle{AOC}\bbox[#ffff00]{=}\angle{OCD}\bbox[#dcff8c]{=}\angle{ODC}\bbox[#ffff00]{=}\angle{ODC}$
$\therefore\; \bbox[#ffff00]{\text{엇각}},\;\bbox[#dcff8c]{\overline{OC}=\overline{OD}}$
[문제]
원 $O$의 지름 $\overline{AB}$ 와 평행한 현 $\overline{CD}$에 대하여 반지름 $\overline{OD}$의 연장선과 원이 만나는 점을 $E$라고 할 때 다음을 만족하는 $\angle{AOD}=x$의 크기를 구하여라.
$\overset{\mmlToken{mo}{⏜}}{EC}:\overset{\mmlToken{mo}{⏜}}{CD}=1:2$
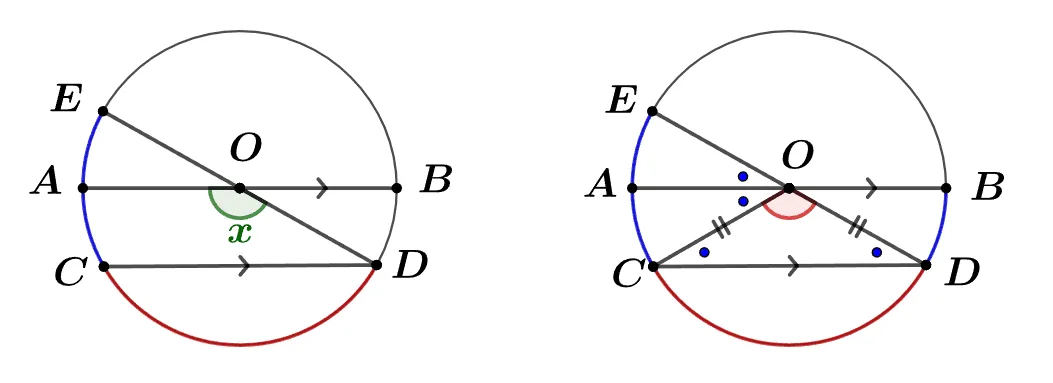
[풀이]
$\angle{OCD}\bbox[#dcff8c]{=}\angle{ODC}\bbox[#ffff00]{=}\angle{AOC}\bbox[#94feff]{=}\angle{EOA}$
$\therefore\;\bbox[#dcff8c]{\overline{OC}=\overline{OD}},\; \bbox[#ffff00]{\text{엇각}},\;\bbox[#94feff]{\text{외각}}$
$\overset{\mmlToken{mo}{⏜}}{EC}:\overset{\mmlToken{mo}{⏜}}{CD}=1:2$
$\quad \xrightarrow[]{\text{정비례}} \; \angle{EOC} : \angle{COD}=1:2$
$\angle{COD}=180^\circ\times \dfrac{2}{3}=120^\circ\\[1em]$
$\angle{AOC}=180^\circ\times \dfrac{1}{3}=60^\circ$
$\therefore\;\angle{AOD}=\dfrac{1}{2}\angle{AOC}+\angle{COD}=150^\circ$
지름과 현의 연장선
[문제]
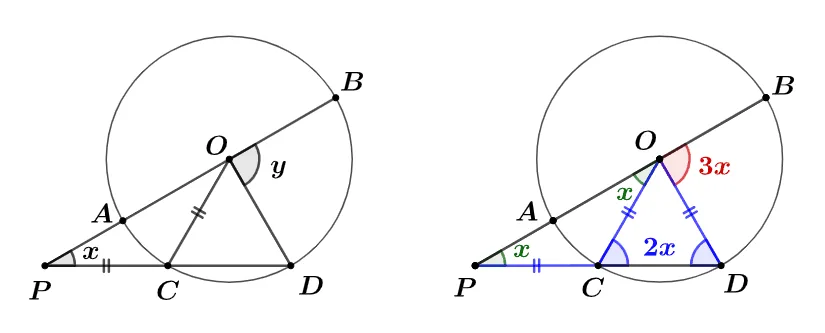
원 $O$의 현$\overline{CD}$의 연장선에 $\overline{PC}=\overline{CO}$ 를 만족하는 점 $P$에 대하여 직선 $\overrightarrow{PO}$와 원 $O$가 만나는 두 점을 $A,\;B$라고 할 때 $\angle{BOD}=y$를 $\angle{CPO}=x$로 나타내라.
[풀이]
$\triangle{COP},\; \triangle{OCD}$가 이등변삼각형 이므로 다음이 성립한다.
$\angle{CPO}=\angle{COP}=x$
$\angle{OCD}=\angle{ODC}=2x$
$\triangle{OCP}$와 평각 $\angle{AOB}=180^\circ$에 대하여
$2x+2x+\bbox[#ffff00]{\angle{COP}}=180^\circ \cdots (1)$
$\angle{AOC}+\angle{BOD}+\bbox[#ffff00]{\angle{COP}}=180^\circ \cdots (2)$
(1), (2)를 정리하면 다음과 같은 결과를 얻을 수 있다.
$\begin{align} \bbox[#dcff8c]{\angle{AOC}}&+\angle{BOD}=4x\\[1em]
&\bbox[#dcff8c]{x}+\angle{BOD}=4x\\[1em]
&\therefore\; \angle{BOD}=3x\end{align}$
[문제]
반지름이 3인 원 $O$의 지름 $\overline{AB}$와 현$\overline{CD}$의 연장선이 만나는 점 $P$에 대하여 $\overline{PC}=\overline{CO}$이다. 색칠한 부채꼴BOD의 넓이가 $\dfrac{9}{4}\pi$일 때 $\overset{\mmlToken{mo}{⏜}}{AC}$의 길이를 구하여라.
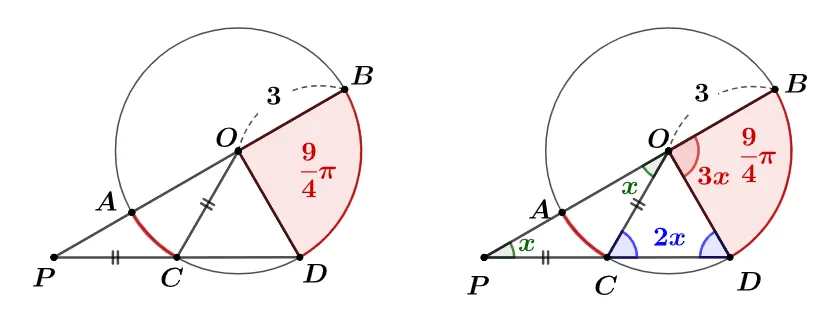
[풀이]
$\overline{PC}=\overline{OC}=\overline{OD}$인 $\triangle{COP},\; \triangle{OCD}$에 대해 삼각형의 내각과 외각의 성질을 적용하면 $\angle{BOD}=3x$이다.
부채꼴 $BOD$의 호의길이 $\bbox[#dcff8c]{l}$과 넓이 $\bbox[#ffff00]{S}$에 대하여
$\bbox[#ffff00]{\dfrac{9}{4} \pi}=\dfrac{1}{2}\times 3\times \bbox[#dcff8c]{l}\\[1em]$
$\bbox[#dcff8c]{l}=\bbox[#ffff00]{\dfrac{9}{4} \pi}\times\dfrac{2}{3}\\[1em]$
$\bbox[#dcff8c]{l}=\dfrac{3}{2}\pi\\[1em]$
호의 길이와 중심각은 정비례 하므로
$\therefore\;\overset{\mmlToken{mo}{⏜}}{AC}=\bbox[#dcff8c]{\dfrac{3}{2}\pi}\times \dfrac{1}{3}=\dfrac{1}{2}\pi$
영역의 넓이
넓이의 합과 차
구할 수 있는 도형의 넓이의 합과 차를 이용하는 유형
[문제그림]
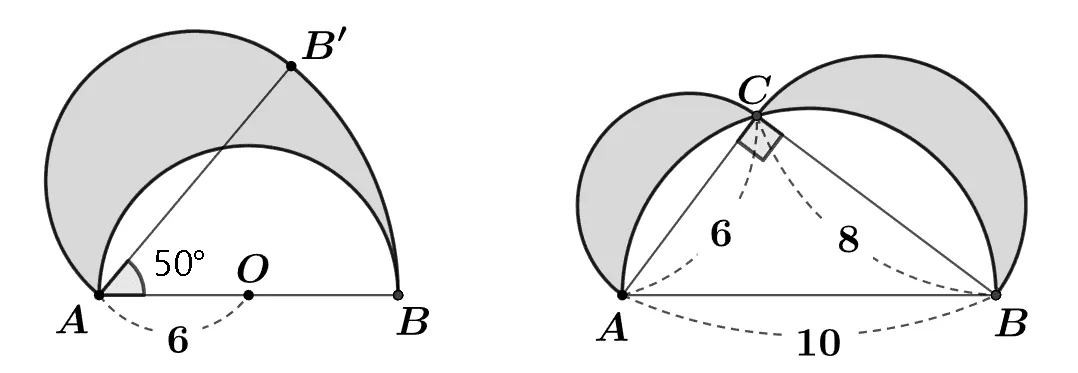
[문제1] 지름이 $\overline{AB}$인 반원을 $A$를 중심으로 $\overset{\mmlToken{mo}{⏜}}{BB’}$를 따라 $50^\circ$회전한 도형에 대하여 색칠한 영역의 넓이를 구하여라.
[문제2] $\angle{ACB}=90^\circ$인 직각삼각형 $\triangle{ABC}$의 세 변$\overline{AB},\;\overline{BC},\; \overline{CA}$를 지름으로 하는 반원에 대하여 색칠된 영역의 넓이를 구하여라.
[풀이그림]
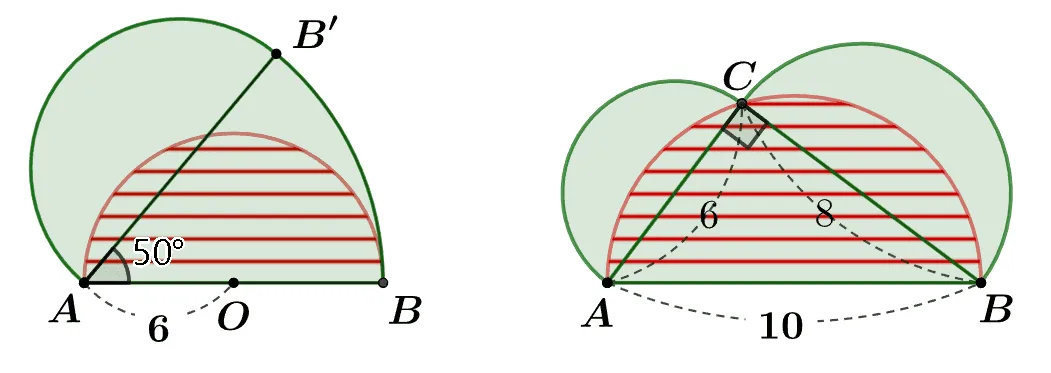
[문제1 풀이]
${\color{green}\text{반원}}+{\color{green}\text{부채꼴 B’AB}}-{\color{red}\text{반원}}$$={\color{green}\text{부채꼴 B’AB}}\\[1em]$
$\begin{align}\therefore\; {\color{green}\text{부채꼴 B’AB}}&=12\times12\pi\times\dfrac{50^\circ}{360^\circ}\\[1em]
&=20\pi\end{align}$
[문제2 풀이]
색칠된 영역의 넓이는 작은 두 반원과 삼각형을 더한 도형에서 큰 반원을 제외한 부분이다. 이를 적용하면 다음과 같이 영역의 넓이를 구할 수 있다.
$\begin{align}&{\color{green}\text{작은 두 반원}}+\bbox[#ffff00]{{\color{green}\triangle{ABC}}}-{\color{red}\text{큰 반원}}\\[1em]
&={\color{green}\dfrac{9\pi}{2}+\dfrac{16\pi}{2}} +\bbox[#ffff00]{{\color{green}\dfrac{1}{2}\times 6\times 8}}-{\color{red}\dfrac{25\pi}{2}}\\[1em]
&=\bbox[#ffff00]{\dfrac{1}{2}\times 6\times 8}\\[1em]
&=24\end{align}$
중학교 2학년 이라면 닮음과 피타고라스 정리를 이용해 다음과 같이 정리해 보길 바란다.
[2번 다른풀이]
직각 삼각형 $\triangle{ABC}$의 세 변 $a, b, c$와 각 변을 지름으로 하는 닮은인 세 원에 대해 가장 긴 변이 $c$일 때 다음이 성립한다.
- 닮음비 : $a:b:c$ $\rightarrow$ 넓이비 : $a^2:b^2:c^2$
- 피타고라스 정리 : $a^2+b^2=c^2$
따라서 작은 두 반원의 넓이의 합은 큰 반원의 넓이와 같다.
$\begin{align}&{\color{green}\text{작은 두 반원}}+\bbox[#ffff00]{{\color{green}\triangle{ABC}}}-{\color{red}\text{큰 반원}}\\[1em]
&=\bbox[#ffff00]{{\color{green}\triangle{ABC}}}\end{align}$
풀이 생략.
합동인 영역 이동
합동인 도형을 찾아 대칭, 평행이동 시켜 넓이를 구하는 유형
[문제]
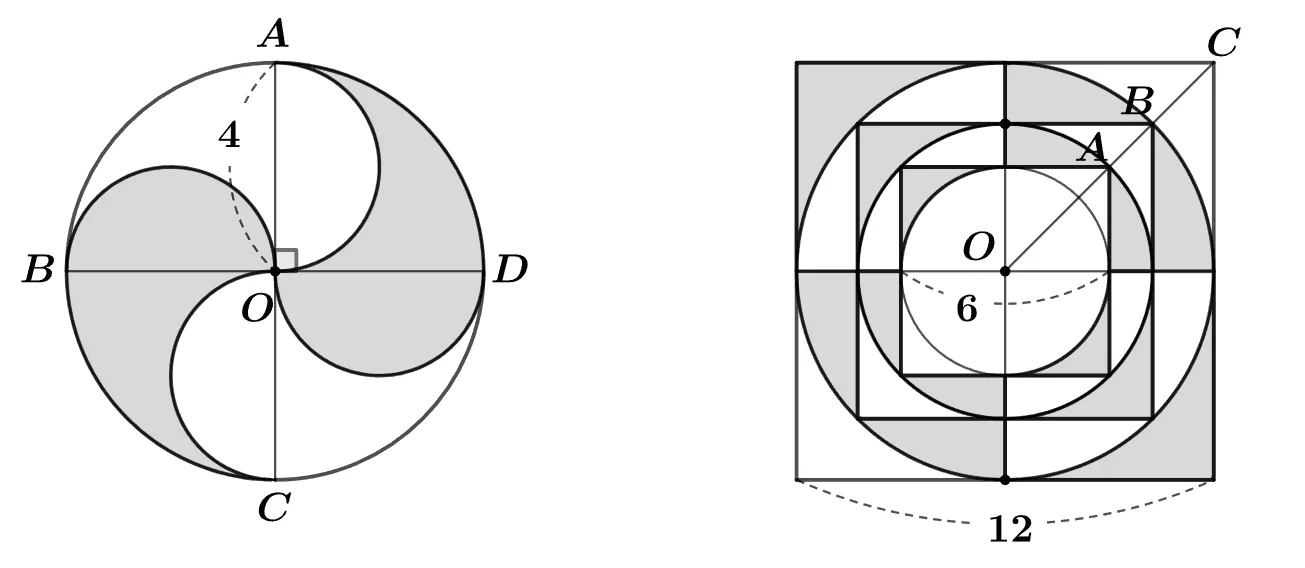
[문제1] 반지름이 4인 원 $O$에 반지름 $\overline{OA},\;\overline{OB},\;\overline{OC},\;\overline{OD}$를 지름으로 하는 반원을 그린 도형에 대하여 색칠한 영역의 넓이를 구하여라.
[문제2] 한 변의 길이가 $6$인 정사각형에 꼭 맞는 지름이 6인 원 $O$를 그린 도형에 $\overline{OA}$를 반지름으로 하는 동심원을 그리고 다시 이 원에 꼭 맞는 정사각형을 각 변이 서로 평행하도록 그리는 과정을 반복한 것이다. 세 번째 정사각형의 한 변의 길이가 $12$일 때 색칠한 영역의 넓이를 구하여라.
[풀이]
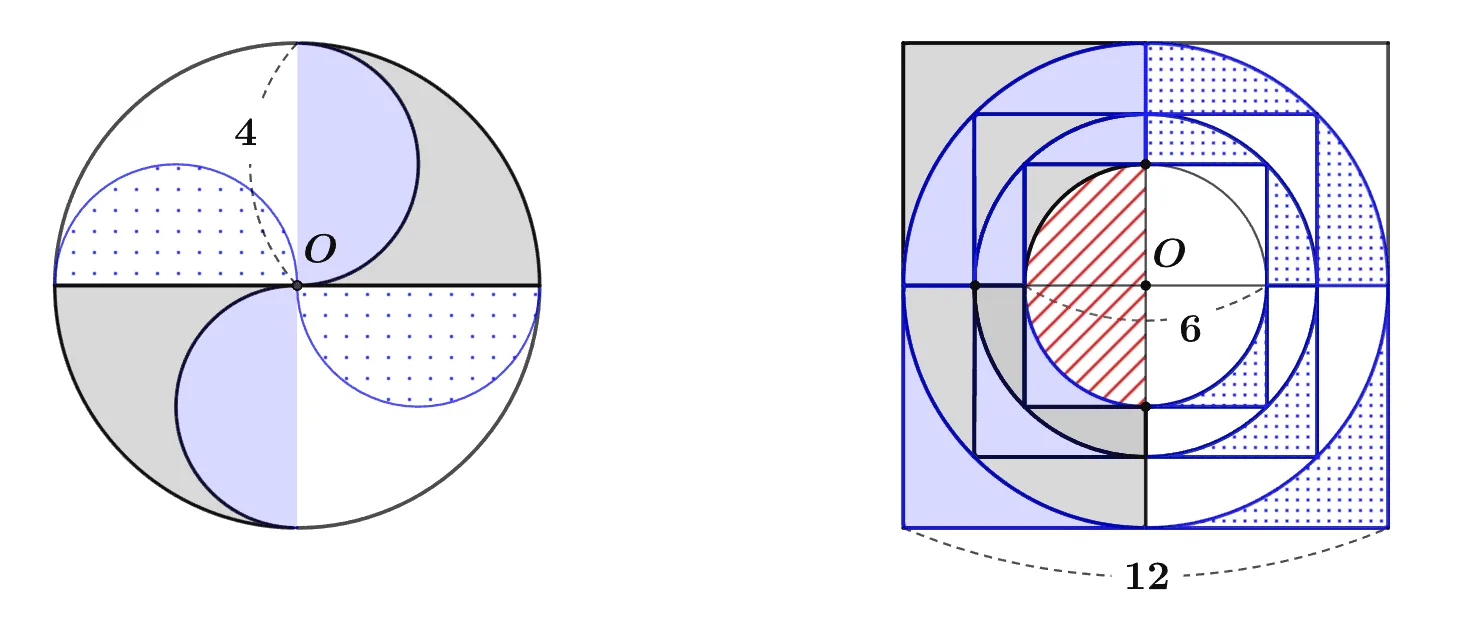
[문제1 풀이]
반원이 서로 합동이 되므로 그림과 같이 이동하여 생각할 수 있다. 따라서 주어진 영역의 넓이는 다음과 같다.
$\bbox[#ffff00]{\text{사분원 넓이}}\times 2=\bbox[#ffff00]{16\pi\times\dfrac{1}{4}}\times 2=8\pi$
[문제2 풀이]
합동인 도형을 한쪽으로 이동하면 위의 그림과 같이 생각할 수 있다. 따라서 넓이는 다음과 같다.
$\begin{align} \bbox[#ffff00]{\text{직사각형}}&-{\color{red}\text{반원}}\\[1em]
&=\bbox[#ffff00]{12\times 6}-{\color{red}9\pi\times\dfrac{1}{2}}\\[1em]
&=72-\dfrac{9\pi}{2}\end{align}
$
영역의 넓이가 같은 문제
동일한 영역의 넓이를 추가하여 넓이를 비교하는 유형
[문제]
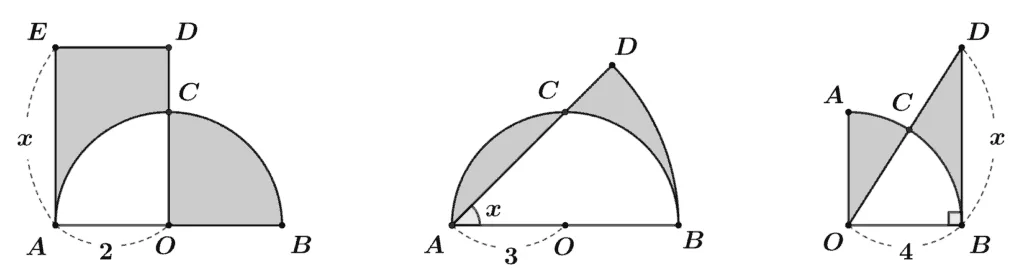
[문제1] 반원 AOB와 직사각형 $\square{AODE}$에 대하여 색칠한 두 영역의 넓이가 같을 때 $\overline{AE}=x$의 길이를 구하여라.
[문제2] 반원 AOB와 부채꼴 DAB에 대하여 색칠한 두 영역의 넓이가 같을 때 $\angle{DAB}=x$의 크기를 구하여라.
[문제3] 사분원 AOB와 직각삼각형 $\triangle{DOB}$에 대하여 색칠한 두 영역의 넓이가 같을 때 $\overline{BD}=x$의 길이를 구하여라.
[풀이]
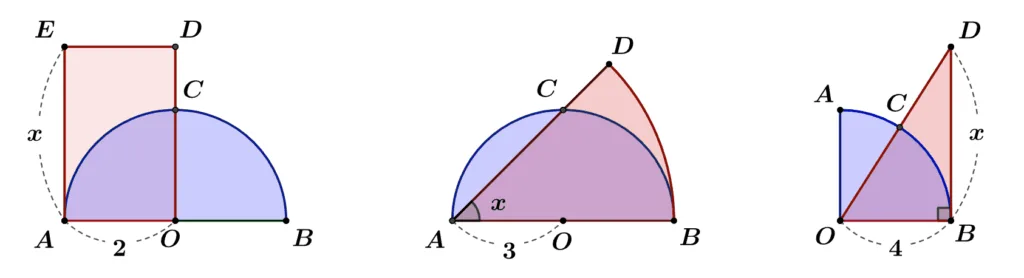
[문제1 풀이]
두 영역에 사분원 AOC을 각 각 포함시켜 생각하면 빨간영역과 파란영역의 넓이가 같음을 알 수 있다.
$\begin{align}{\color{blue}\text{반원 넓이}}&={\color{red}\square{AOBE}\text{ 넓이}}\\[1em]
{\color{blue}\dfrac{1}{2}\times4\pi}&={\color{red}2x}\\[1em]
\therefore\; x=\pi \end{align}$
[문제2 풀이]
두 영역에 $\overset{\mmlToken{mo}{⏜}}{BC},\;\overline{AB},\;\overline{AC}$로 둘러싸인 영역을 각 각 포함시키면 파란 영역과 빨간 영역의 넓이가 같음을 알 수 있다.
$\begin{align}{\color{blue}\text{반원 넓이}}&={\color{red}\text{부채꼴 DAB 넓이}}\\[1em]
{\color{blue}\dfrac{1}{2}\times9\pi}&={\color{red}36\pi\times\dfrac{x^\circ}{360^\circ}} \end{align}$
$\begin{align} \therefore x&={\color{blue}\dfrac{1}{2}\times9\pi}\times{\color{red}\dfrac{360^\circ}{36\pi}}\\[1em]
&=45^\circ\end{align}$
[문제3 풀이]
두 영역에 부채꼴 COD의 넓이를 각 각 포함 시키면 파란 영역과 빨간 영역의 넓이가 같다.
$\begin{align}{\color{blue}\text{사분원 넓이}}&={\color{red}\triangle{DOB}\text{ 넓이}}\\[1em]
{\color{blue}\dfrac{1}{4}\times16\pi}&={\color{red}\dfrac{1}{2}\times 4 \times x}\end{align}$
$\therefore \;x=\dfrac{16\pi}{4}\times\dfrac{2}{4}=2\pi$
심화 문제
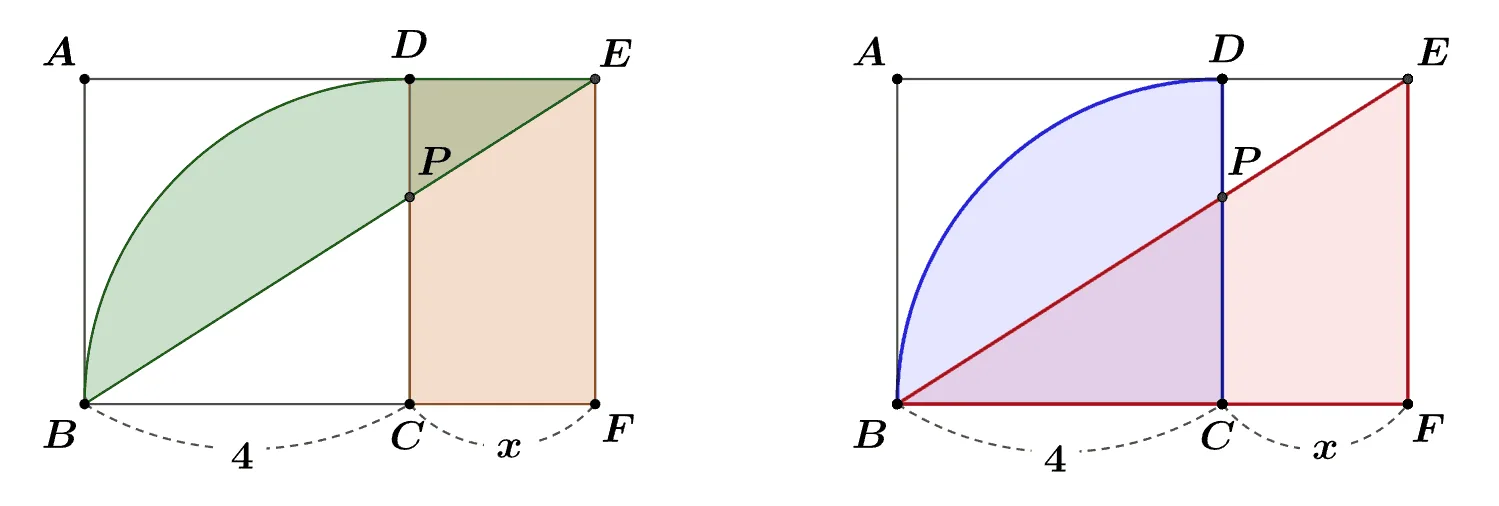
[문제]
한 변의 길이가 4인 정사각형 $\square{ABCD}$와 직사각형 $\square{DCFE}$에 대하여 ${\color{green}\text{색칠된 도형}}$의 넓이가 $\square{DCFE}$와 같을 때 $\overline{CF}=x$의 길이를 구하여라.
[풀이]
${\color{green}\text{색칠된 도형}}$과 $\square{DCFE}$의 공통 영역 $\triangle{DEP}$를 제외한 영역에 $\triangle{PBC}$를 각 각에 포함시키면 파란 영역과 빨간 영역의 넓이가 같다.
$\begin{align} {\color{blue}\dfrac{1}{4}\times16\pi}&={\color{red}\dfrac{1}{2}\times(4+x)\times 4}\\[1em]
{\color{blue}4\pi}&={\color{red}8+2x}\end{align}$
$\therefore\; x=2\pi-4$
정삼각형 작도 관련 문제
정삼각형 작도 관련 사실
먼저 정삼각형의 작도와 관련된 사실에 대해 다음 두 문제를 이용해 정리하자.
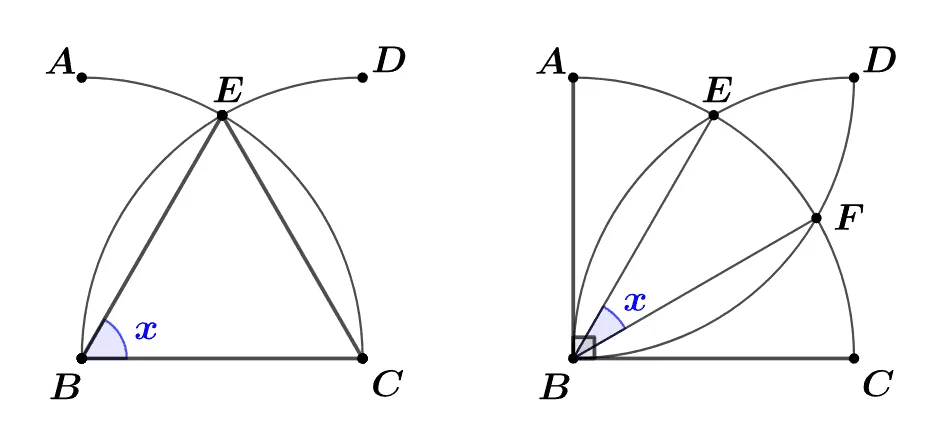
[문제1] 자와 컴퍼스를 이용해 작도한 도형이다. $\triangle{EBC}$가 정삼각형 임을 보여라.
[문제2] 중심각이 $90^\circ$인 부채꼴ABC에 대하여 반지름이 같고 중심이 $C,\;A$인 사분원이 $\overset{\mmlToken{mo}{⏜}}{AC}$와 만나는 점을 각 각 $E,\;F$라고 할 때 $\angle{EBF}=30^\circ$임을 보여라.
[풀이]
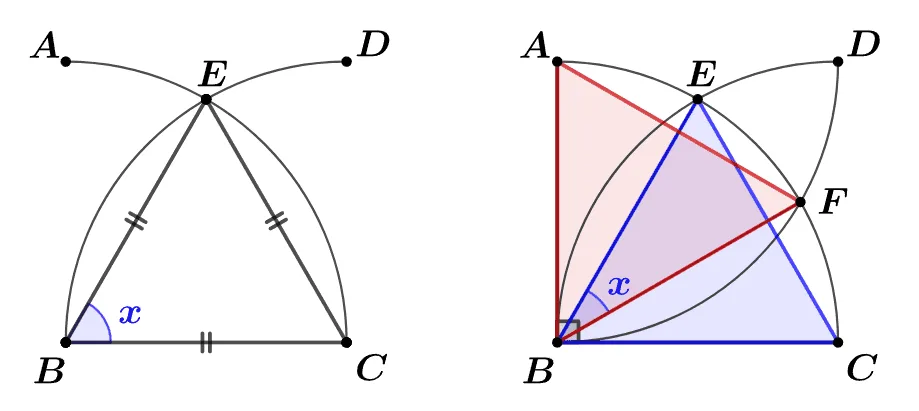
[문제1 풀이]
$\overline{BE}=\overline{CE}=\overline{BC}$(반지름)이고 따라서$\triangle{EBC}$는 정삼각형이다.
$\angle{EBC}=\angle{BCE}=\angle{CEB}=60^\circ$라는 사실도 추가로 알 수 있다.
[문제2 풀이]
$\triangle{EBC},\;\triangle{ABF}$는 세변의 길이가 반지름으로 같은 정삼각형이다.
$\angle{ABE}=\angle{FBC}=30^\circ\\[1em]$
$\therefore\; \angle{EBF}=30^\circ$
정삼각형 작도 관련 문제
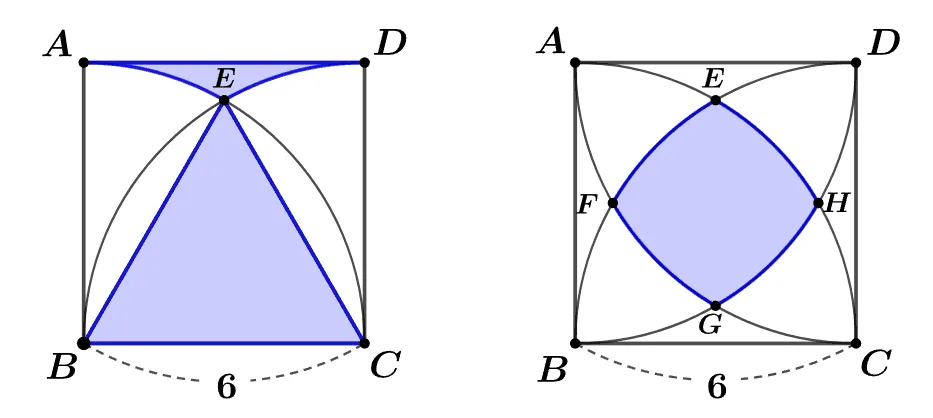
[문제1] 한 변의 길이가 $6$인 정사각형 $\square{ABCD}$의 두 꼭짓점 $B,\; C$를 중심으로 반지름이 $6$인 사분원을 그리고 두 원의 교점을 $E$라고 할 때 색칠된 도형의 넓이를 구해라.
[문제2] 한 변의 길이가 $6$인 정사각형 $\square{ABCD}$의 네 꼭짓점에서 반지름이 $6$인 사분원을 그리고 네 사분원의 교점을 $E,\;F,\;G,\;H$라고 할 때 색칠된 도형의 둘레를 구하여라.
[풀이 그림]
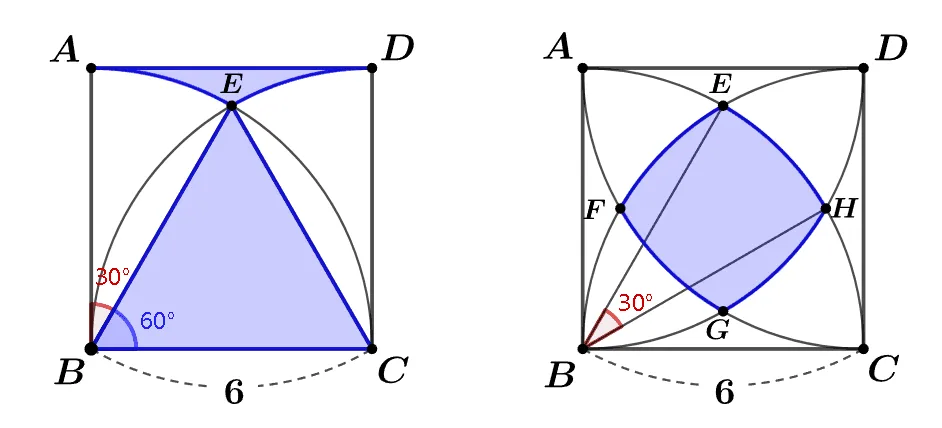
[문제1 풀이]
$\triangle{EBC}$는 정삼각형 이므로 $\angle{ABE}=\angle{ECD}=30^\circ$이다.
색칠되지 않은 부분이 부채꼴이므로 다음과 같이 넓이를 구할 수 있다.
$\begin{align}{\color{blue}\text{파란색 도형}}&=\square{ABCD}-\text{색칠되지 않은 도형}\\[1em]
&=36-6^2\pi\times\dfrac{30}{360}\times2\\[1em]
&=36-6\pi\end{align}$
따라서 색칠된 도형의 넓이는 $36-6\pi$ 이다.
[문제2 풀이]
$\triangle{EBC},\;\triangle{ABH}$은 정삼각형 이므로 다음이 성립한다.
- $\angle{EBC}=\angle{ABH}=60^\circ$
- $\angle{ABE}=\angle{HBC}=30^\circ$
- $\angle{EBH}=30^\circ$
중심각이 $30^\circ$인 호의 길이에 대하여
- $\overset{\mmlToken{mo}{⏜}}{EH}=\overset{\mmlToken{mo}{⏜}}{HG}=\overset{\mmlToken{mo}{⏜}}{GF}=\overset{\mmlToken{mo}{⏜}}{FE}$
- $\overset{\mmlToken{mo}{⏜}}{FE}=(2\times6\times\pi)\times\dfrac{30}{360}=\pi$
따라서 색칠된 도형의 둘레는 $4\pi$ 이다.
정사각형과 내부 반원 문제
정사각형과 반원에 대한 사실
먼저 당연해 보이는 두 가지 사실에 대해 문제를 통해 정리해 보기로 하자.
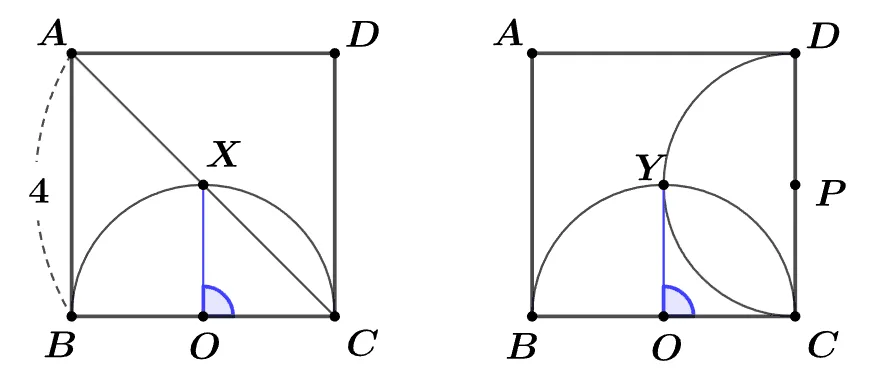
[문제1] 정사각형 $\square{ABCD}$의 대각선 $\overline{AC}$와 $\overline{BC}$를 지름으로 하는 반원 $O$가 만나는 교점을 $X$라고 할 때 $\angle{XOC}$의 크기를 구하여라.
[문제2] 정사각형 $\square{ABCD}$에서 $\overline{BC},\; \overline{CD}$를 지름으로 하는 두 반원 $O,\; P$의 교점 $Y$에 대하여 $\angle{YOC}=90^\circ$임을 보여라.
[풀이]
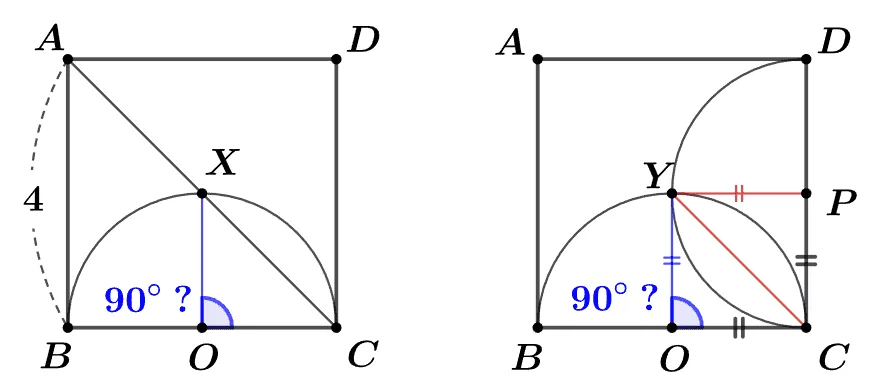
[문제1 풀이]
$\triangle{ABC}\equiv\triangle{ADC}$ (SAS 합동)
$\angle{XCO}=45^\circ$
$\overline{OX}=\overline{OC}$(반지름)
$\angle{OCX}=\angle{OXC}=45^\circ$
$\therefore \; \angle{XOC}=90^\circ$
[문제2 풀이]
보조선 $\overline{YP}$, $\overline{YC}$에 대하여
$\triangle{YOC}\equiv\triangle{YPC}$(SSS 합동)
$\angle{YCP}=\angle{YCO}=45^\circ$ (직각)
$\angle{YCO}=\angle{COY}=45^\circ$ (이등변삼각형)
$\therefore\; \angle{YOC}=90^\circ$
문제 1, 2의 사실을 정리하면
$\triangle{CXO}\equiv\triangle{CYO}$
$\therefore\;X=Y$
따라서 반원의 교점은 대각선 위에 있음을 알 수 있다.
정사각형과 반원에 대한 문제
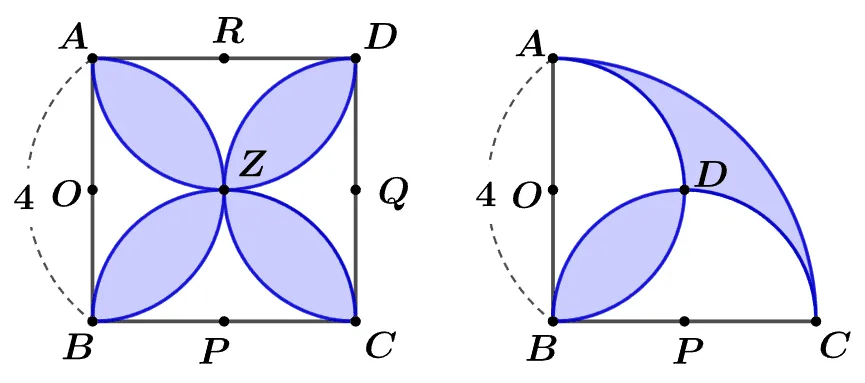
[문제1] 정사각형 $\square{ABCD}$에서 $\overline{AB},\;\overline{BC},\; \overline{CD},\;\overline{DA}$를 지름으로 하는 반원 $O,\; P,\;Q,\;R$의 교점 $Z$에 대하여 $\overline{AB}=4$일 때 색칠된 도형의 넓이를 구하여라.
[문제2] 반지름이 $4$인 사분원의 두 반지름 $\overline{AB},\;\overline{BC}$를 지름으로 하는 두 반원 $O,\;P$의 교점을 $D$라고 할 때 색칠된 도형의 넓이를 구하여라.
[풀이]
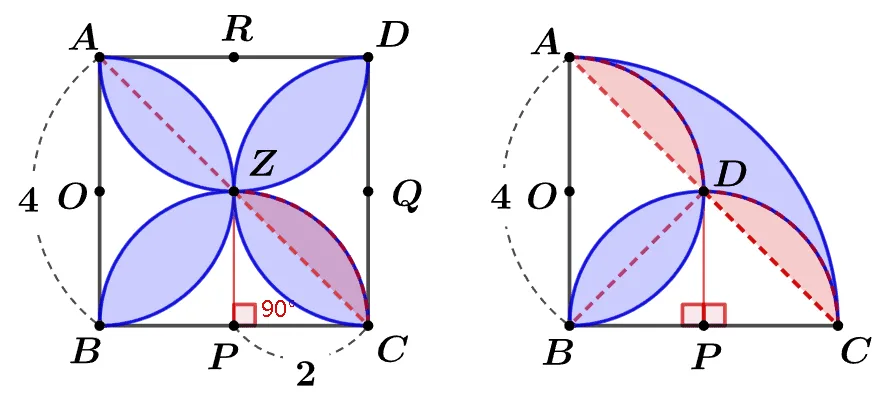
[문제1 풀이]
$\begin{align} {\color{red}\text{빨간 영역}}&=\bbox[#ffff00]{\text{부채꼴 ZPC}}-\bbox[#dcff8c]{\triangle{ZPC}}\\[1em]
&=\bbox[#ffff00]{4\pi\times\dfrac{90^\circ}{360^\circ}}-\bbox[#dcff8c]{\dfrac{1}{2}\times2\times2}\\[1em]
&=\pi-2\end{align}$
$\therefore\; {\color{blue}\text{파란 영역}}={\color{red}(\pi-2)}\times 8=8\pi-16$
[문제2 풀이]
$\angle{BPD}=\angle{DPC}=90^\circ$
$\text{부채꼴 BPD}\equiv\text{부채꼴 DPC}$
따라서 쌀알 모양을 $\overline{BD}$로 나누어 빨간 영역으로 옮겨 아래와 같이 계산 할 수 있다.
$\begin{align} {\color{blue}\text{파란 영역}}&=\bbox[#ffff00]{\text{부채꼴ABC}}-\bbox[#dcff8c]{\triangle{ABC}}\\[1em]
&=\bbox[#ffff00]{16\pi\times\dfrac{90^\circ}{360^\circ}}-\bbox[#dcff8c]{\dfrac{1}{2}\times 4\times4}\\[1em]
&=4\pi-8\end{align}$
$\therefore\; {\color{blue}\text{파란 영역}}=4\pi-8$
도형의 자취 문제
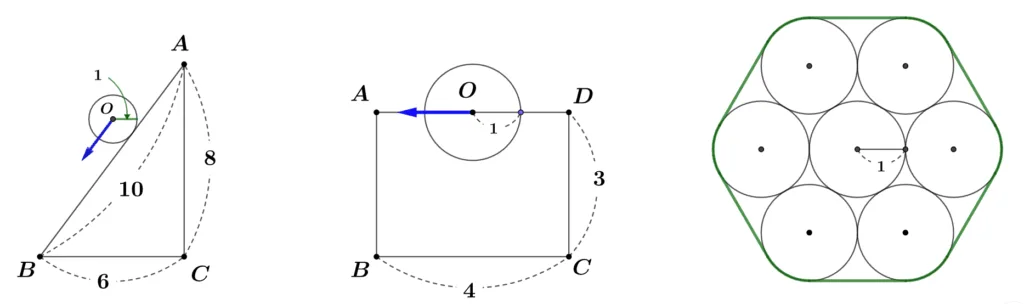
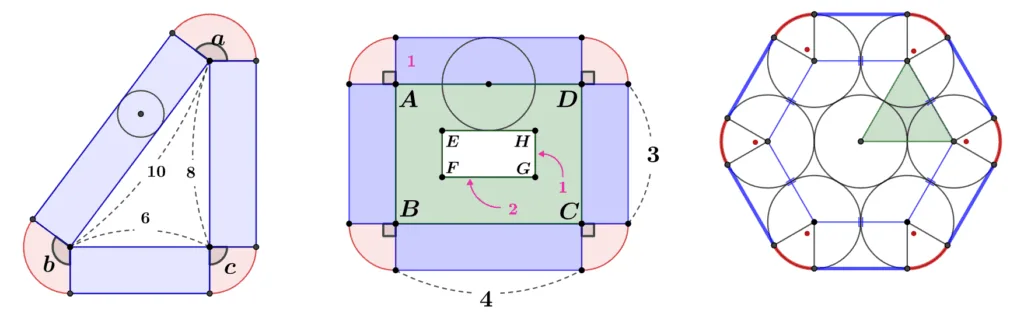
[문제1] $\triangle{ABC}$의 둘레를 반지름이 1인 원 $O$가 돌고 있다. 원 한 바퀴 돌 때 원이 지나간 자리의 넓이를 구하여라.
[문제2] 중심 $O$가 직사각형 $\square{ABCD}$의 변위에 있는 반지름이 1인 원에 대하여 원이 변을 따라 한 바퀴 돌 때 지나간 자리의 넓이를 구하여라.
[문제3] 반지름이 1인 원형 통나무 7개를 그림과 같이 묶을 때 필요한 끈의 최소 길이를 추측하려고 한다. 녹색 곡선의 둘레를 계산하여라.
[풀이]
[문제1 풀이]
원이 이동하면서 만들어진 영역은 삼각형의 각 변에서 지름의 길이 만큼 이다.
$\begin{align}&({\color{blue}\text{직사각형}})+({\color{red}\text{부채꼴}})\\[1em]
&=({\color{blue}10\times2+8\times2+6\times2})+({\color{red}4\pi})\\[1em]\end{align}$
$\therefore\; 48+4\pi$
[문제2 풀이]
원이 이동하면서 만들어진 영역은 사각형의 변위의 점에서 양쪽으로 반지름의 길이 만큼 이다.
$\begin{align}&({\color{blue}\text{직사각형}})+({\color{green}\text{직사각형}})+({\color{red}\text{부채꼴}})\\[1em]
&({\color{blue}4+3+4+3})+({\color{green}12-2})+({\color{red}\pi})
\end{align}$
$\therefore\; 24+\pi$
[문제3 풀이]
인접한 세 원의 중심을 연결한 ${\color{green}\text{녹색 삼각형}}$은 세 변의 길이가 2인 정삼각형이다. 따라서 바깥쪽 원의 중심을 연결한 도형은 한 변의 길이가 2인 정육각형이다.
$\begin{align}&({\color{blue}\text{정 육각형 둘레}})+({\color{red}\text{부채꼴의 호}})\\[1em]
&=({\color{blue}2\times6})+({\color{red}2\pi})\end{align}$
$\therefore\; 12+2\pi$
회전 도형의 자취
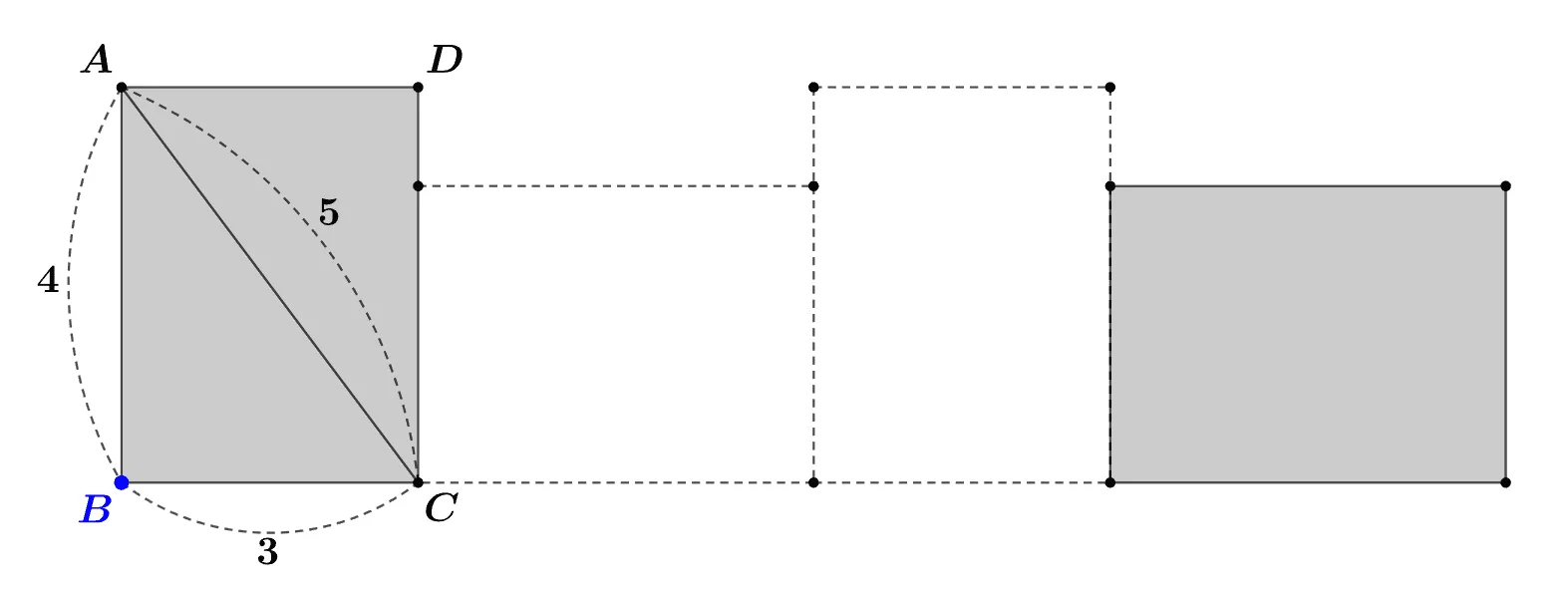
[문제] 두 변의 길이와 대각선의 길이가 각 각 $3, 4, 5$인 직사각형 $\square{ABCD}$를 $\overrightarrow{BC}$ 위에서 3번 회전시킬 때 점 ${\color{blue}B}$가 움직인 거리를 구하여라.
[풀이]
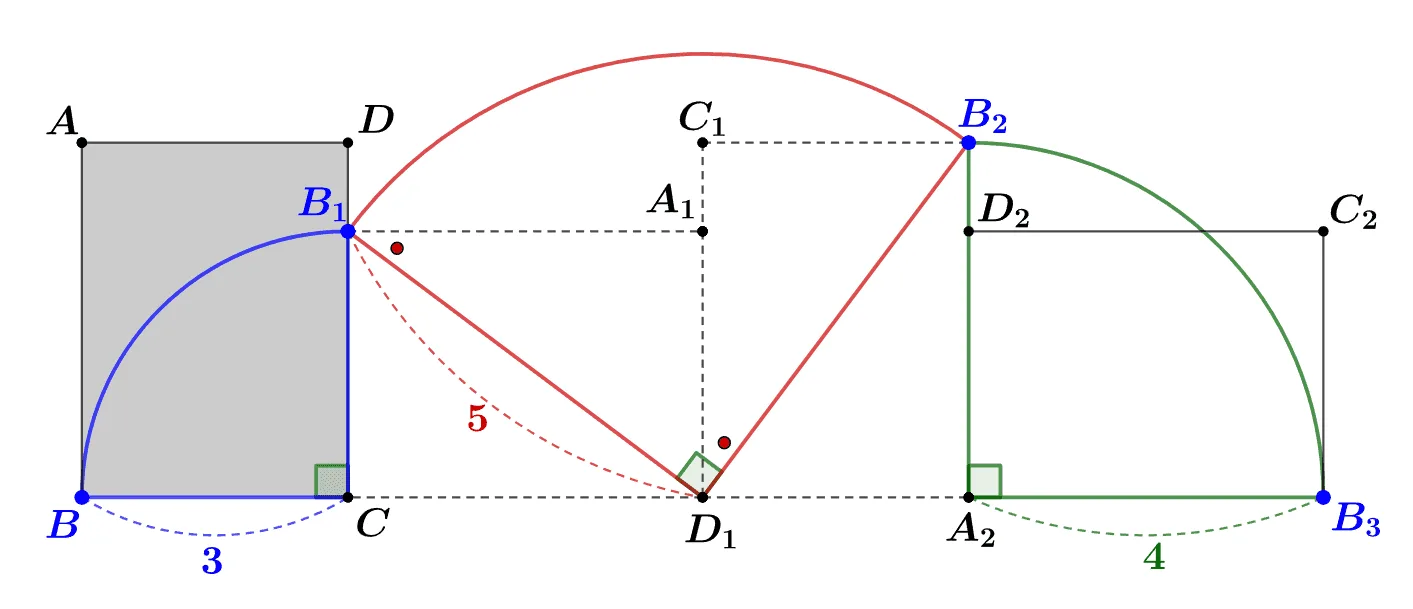
점 ${\color{blue}B}$가 회전하면서 움직인 거리는 다음과 같다.
$\begin{align}&({\color{blue}\overset{\mmlToken{mo}{⏜}}{BB_1}})+({\color{red}\overset{\mmlToken{mo}{⏜}}{B_1B_2}})+({\color{green}\overset{\mmlToken{mo}{⏜}}{B_2B_3}})\\[1em]
&({\color{blue}\dfrac{1}{4}\times6\pi})+({\color{red}\dfrac{1}{4}\times10\pi})+({\color{green}\dfrac{1}{4}\times8\pi})
\end{align}$
$\therefore\; 6\pi$
이상으로 원과 부채꼴에 대한 문제풀이를 마무리 하겠습니다.