이번 시간에는 상대도수분포표를 이용해 도수의 총합이 다른 두 집단을 공정하게 비교하는 방법에 대해 다루었습니다. 상대도수를 이용한 도수분포다각형으로 두 집단의 경향성을 분석하는 과정을 통해 상대도수의 필요성에 대해 생각하는 시간이 되길 바랍니다.
개요
상대도수
도수의 총합이 다른 두 집단을 비교하기 위해 계급의 상대도수를 다음과 같이 정의하여 사용한다.
- $(\text{계급의 상대도수})=\dfrac{(\text{계급의 도수)}}{(\text{도수의 총합})}$
[상대도수의 필요성]
- 집단의 크기 차이를 제거 $\rightarrow$ 두 집단의 공정한 비교
[상대도수 변형식]
- $(\text{계급의 도수})=(\text{상대도수}) \times (\text{도수의 총합})$
- $(\text{도수의 총합})=\dfrac{(\text{계급의 도수})}{(\text{상대도수})}$
상대도수분포표
도수분포표를 이용해 상대도수를 구하는 과정은 다음과 같다.
| 계급 (점수) | 도수 | 상대도수 |
|---|---|---|
| 50$^\text{이상}$~ 59$^\text{미만}$ | 5 | $\dfrac{5}{50}=0.10$ |
| 60 ~ 69 | 10 | $\dfrac{10}{50}=0.20$ |
| 70 ~ 79 | 15 | $\dfrac{15}{50}=0.30$ |
| 80 ~ 89 | 12 | $\dfrac{12}{50}=0.24$ |
| 90 ~ 99 | 8 | $\dfrac{8}{50}=0.16$ |
| 합계 | 50 | 1.00 |
위의 과정을 통해 다음과 같은 사실을 알 수 있다.
상대도수 성질
- (상대도수 총합) $=1$
\begin{flalign}
&\dfrac{\textcolor{blue}{5+10+15+12+8}}{50}\\[1em]
&\dfrac{\textcolor{blue}{\text{도수의 총합}}}{50}\\[1em]
&=1
&&\end{flalign} - (상대도수) $\propto$ (계급의 도수)
분수식과 정비례 , 반비례 관계
$\bbox[#ffff00]{A}=\dfrac{\bbox[#ffff00]{X}}{Y}$에 대하여
$Y$가 일정 할 때 $\bbox[#ffff00]{A,X}$는 $\bbox[#ffff00]{\text{ 서로 정비례}}$
$\bbox[#dcff8c]{A}=\dfrac{X}{\bbox[#dcff8c]{Y}}$에 대하여
$X$가 일정 할 때 $\bbox[#dcff8c]{A,Y}$는 $\bbox[#dcff8c]{\text{ 서로 반비례}}$
두 집단의 비교
도수의 총합이 다른 $A,\;B$반의 단원평가 점수를 도수와 상대도수를 이용해 나타낸 표이다. 자료에서 상위권을 비교하는 공정한 방법으로서 상대도수의 필요성을 정리해 보자.
| 점수 (계급) | A반 (명) | A반 상대 도수 | B반 (명) | B반 상대 도수 |
|---|---|---|---|---|
| 0$^\text{이상}$~ 8$^\text{미만}$ | 3 | 0.15 | 4 | 0.16 |
| 8 ∼ 16 | 4 | 0.20 | 6 | 0.24 |
| 16 ∼ 24 | 4 | 0.20 | 5 | 0.20 |
| 24 ∼ 32 | 5 | 0.25 | 6 | 0.24 |
| 32 ∼ 40 | 4 | 0.20 | 4 | 0.16 |
| 합계 | 20 | 1.00 | 25 | 1.00 |
상대도수의 필요성
- 24$^\text{이상}$~ 40$^\text{미만}$인 학생 수
- A반 : 9명, B반 :10명
단순히 학생수가 많다고 B반이 잘한다고 할 수 있을까? 집단의 크기가 다르기 때문에 공정하다고 볼 수 없다. 따라서 공정하게 비교하기 위해 상대도수를 이용할 필요가 있다.
상대도수 특징과 제한점
특징
- 상대도수 총합 : 1
- 상대도수는 계급의 도수에 정비례
- 도수의 총합이 다른 두 집단의 공정한 비교
제한점
- 한 눈에 자료의 경향성을 확인하기 어려움
상대도수, 히스토그램?
- 상대도수 : 두 집단의 비교할 때 사용
- 히스토그램 : 두 집단의 비교에 적절하지 않음.
위와 같은 이유로 상대도수를 이용해 히스토그램을 그리는 활동은 실제와 전혀 맞지 않다.
따라서 여기서는 도수분포다각형을 통해 두 집단을 비교하는 과정에 대해서만 살펴보도록 하겠습니다. 일반적인 도수에서 내용은 아래의 포스팅을 참고해 주세요.
상대도수를 이용한 도수분포다각형
도수분포다각형은 두 집단의 분포를 비교하는 시각적인 도구이다. 특히 두 집단의 크기가 서로 다른 경우 상대도수를 이용해 도수분포다각형을 만들면 전체적인 경향성을 공정하게 비교할 수 있다.
$\textcolor{red}{\text{계급값}}$을 이용하면 히스토그램을 그리지 않고 도수분포다각형을 그릴 수 있다.
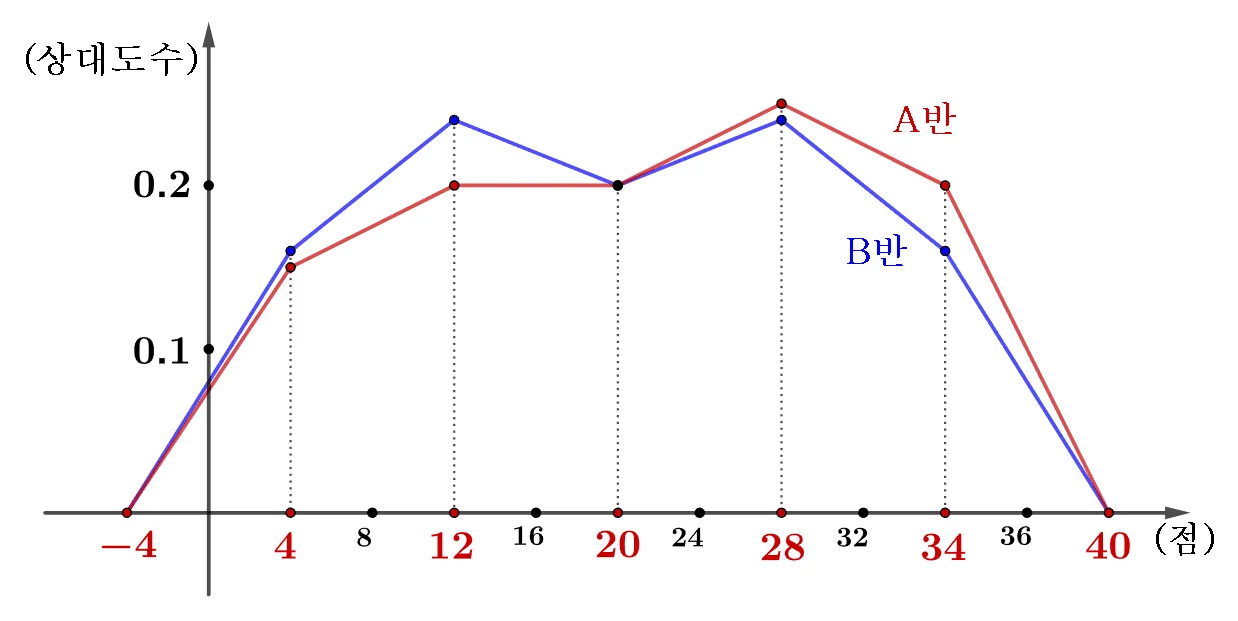
이를 통해 다음과 같은 사실을 알 수 있다.
- A반은 상위권 학생의 비율이 높다.
- B반은 A반보다 성적이 고르다.
특징과 제한점
특징
- 상대도수 $\rightarrow$ 공정한 비교
- 두 집단의 분포와 경향성을 한 눈에 비교
- $(\text{상대도수분포다각형의 면적})=(\text{계급의 크기})$
\begin{flalign}
\because \; &(\text{상대도수분포다각형의 면적})\\[1em]
&=(\text{계급의 크기}) \times (\text{상대도수 총합}) \\[1em]
&=(\text{계급의 크기}) \times (1)\\[1em]
&=(\text{계급의 크기})
&&\end{flalign}
제한점
- 도수에 대한 정보 없음 (비율로 표현)
중고등학교 통계 프로그램 사이트
중고등학교 통계수업에 활용할 수 있는 프로그램을 제공하는 사이트 입니다.