삼각형의 합동조건 이등변삼각형 성질 증명

삼각형의 합동조건 이등변삼각형 성질 조건 증명

by

삼각형의 합동조건은 중학교 기하를 다루는데 매우 중요한 도구입니다. 이번 시간에는 도형의 합동에 대한 이론과 삼각형의 합동조건에 대해 정리하고 이를 토대로 초등학교 에서 배운 이등변삼각형의 성질을 합동조건을 이용해 증명하는 과정을 다루었습니다.

학습지 다운로드

도형의 합동

도형의 합동 : 두 도형이 완전히 포개어 질 때 서로 합동이라고 한다

  • 기호 : (도형1)$\equiv$ (도형2)
  • 대응 : 합동인 두 도형에서 서로 포개어 지는 꼭짓점, 변, 각은 서로$\bbox[#ffff00]{\text{대응한다}}$라고 한다.
    • 대응하는 꼭짓점, 변, 각 $\rightarrow$ 대응점, 대응변, 대응각

합동인 도형의 성질

두 도형이 합동이면 다음 성질이 성립한다.

  1. 대응각의 크기가 같다.
  2. 대응변의 길이가 같다.
  3. 넓이가 같다.

삼각형의 합동

합동인 삼각형 용어 정리

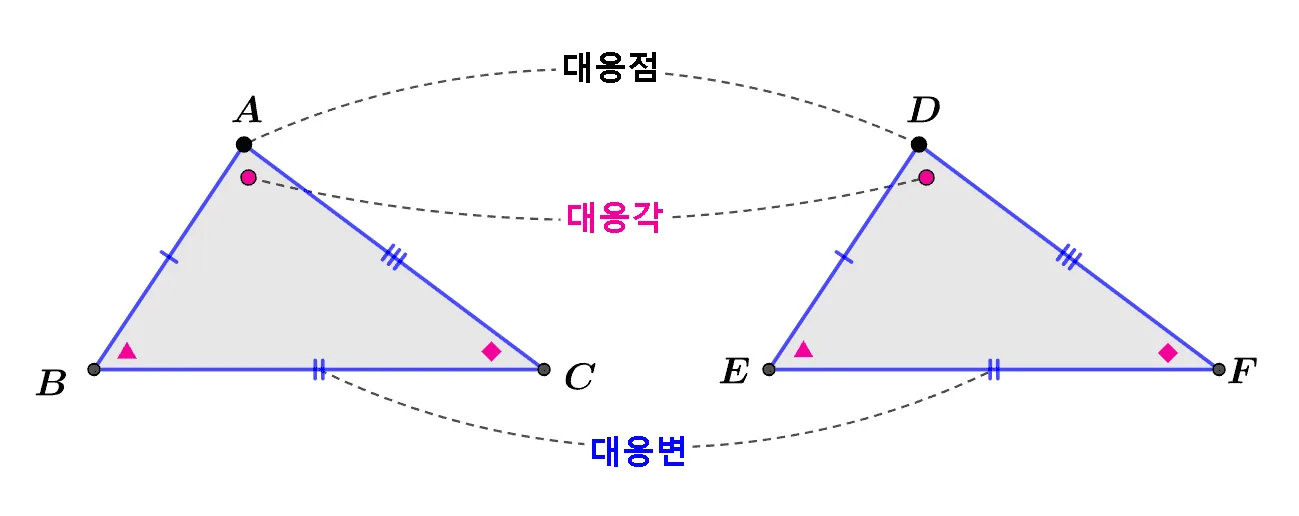
위의 합동인 삼각형 $\triangle{ABC}$와 $\triangle{DEF}$에서 대응점, 대응각, 대응변은 다음과 같다.

  • 대응점: $(\bbox[#ffff00]{A,D}),\;(\bbox[#dcff8c]{B,E}),\;(\bbox[#94feff]{C,F})$
  • 대응각: $(\angle{A},\angle{D})$, $(\angle{B},\angle{E})$, $(\angle{C},\angle{F})$ 크기가 같다.
  • 대응변: $(\overline{AB},\overline{DE})$, $(\overline{BC},\overline{EF})$, $(\overline{CA},\overline{FD})$ 길이가 같다.

위와 같이 $\triangle{ABC}$와 $\triangle{DEF}$가 합동임을 나타내는 기호는 아래와 같다.

  • 기호 : $\triangle{\bbox[#ffff00]{A}\bbox[#dcff8c]{B}\bbox[#94feff]{C}}\equiv\triangle{\bbox[#ffff00]{D}\bbox[#dcff8c]{E}\bbox[#94feff]{F}}$ (대응점 순서 일치)

합동기호와 등호는 서로 다른 의미로 사용되므로 주의하자.

  • $\triangle{ABC}\equiv\triangle{DEF}$ : 합동이다.
  • $\triangle{ABC}=\triangle{DEF}$ : 넓이가 같다.

합동과 넓이에 대하여 다음이 성립한다.

  • $\triangle{ABC}\equiv\triangle{DEF}$ 이면 $\triangle{ABC}=\triangle{DEF}$이다.
  • $\triangle{ABC}=\triangle{DEF}$ 라고 해서 $\triangle{ABC}\equiv\triangle{DEF}$인 것은 아니다.

삼각형의 합동조건

작도를 통해 학습했던 삼각형이 하나로 결정될 조건은 다음과 같다.

  1. 세 변의 길이가 주어진 경우
    • (가장 긴 변 길이)$<$(나머지 변의 합)
  2. 두 변의 길이와 끼인각의 크기
  3. 한 변의 길이와 양 끝각의 크기
    • (양 끝각의 합)$<180^\circ$

위의 조건중 하나가 주어지면 삼각형은 오직 하나로 결정된다(작도된다). 따라서 두 삼각형이 세 가지 조건 중 하나를 동시에 만족한다면 두 삼각형은 서로 정확히 겹쳐진다, 즉 합동이다.

이를 토대로 두 삼각형의 합동조건을 정리하면 다음과 같다.

  1. 세 쌍의 대응변의 길이가 각각 같을 때 ($\bbox[#ffc5fd]{SSS}$ 합동)
  2. 두 쌍의 대응변의 길이가 각각 같고 $\bbox[#ffff00]{\text{끼인각}}$의 크기가 같을 때 ($\bbox[#ffc5fd]{SAS}$ 합동)
  3. 한 쌍의 대응변의 길이가 같고 $\bbox[#ffff00]{\text{양 끝각}}$의 크기가 각각 같을 때 ($\bbox[#ffc5fd]{ASA}$ 합동)

매번 조건을 서술하기 번거롭기 때문에 변(Side), 각(Angle)의 머릿글자 S, A를 따서 각 합동조건을 $\bbox[#ffc5fd]{SSS}, \bbox[#ffc5fd]{SAS}, \bbox[#ffc5fd]{ASA}$ 로 표현하기로 하자.

합동조건을 시각적으로 아래와 같이 표현하고 암기하는 것이 편하다.

삼각형의 합동조건 SSS SAS ASA

이등변삼각형의 성질 조건

초등학교에서 두 변의 길이가 같은 삼각형을 이등변삼각형으로 배웠고, 다음과 같은 사실을 종이접기를 통해 직관적으로 학습하였다. 이등변삼각형의 정의를 이용해 아래의 두 성질에 대해 증명해 보기로 하자.

  • 이등변삼각형 : 두 변의 길이가 같은 삼각형
    1. 성질: 이등변삼각형은 두 밑각의 크기가 같다.
    2. 조건: 두 밑각의 크기가 같으면 이등변삼각형이다.

합동을 학습하면 위의 두 가지 사실에 대해 증명할 수 있다. 전반적인 사고는 중학교 2학년 수준이지만 합동인 삼각형을 찾아 증명하는 과정은 1학년 수준에서 학습할 수 있으므로 합동조건을 적용해 증명해 보자.

이등변삼각형의 성질 증명

1.이등변삼각형은 두 밑각의 크기가 같다.

이등변삼각형의 성질 증명

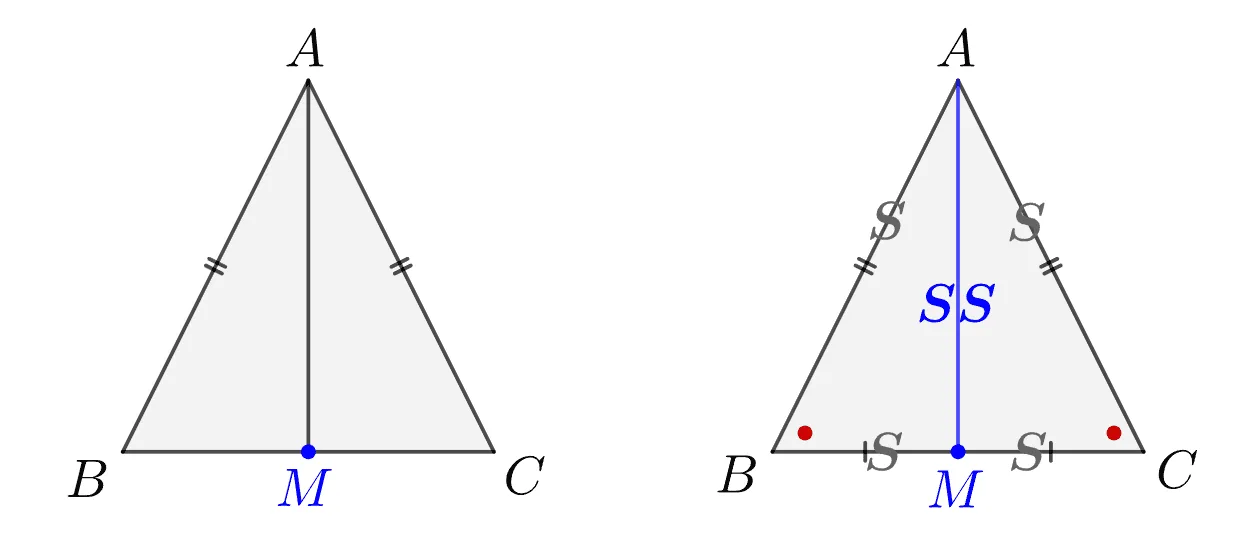
[증명]

증명의 핵심은 $\overline{BC}$의 중점 $M$에 대해 보조선 $\overline{AM}$을 그리는 것이다. 이 후 과정은 중학교 1학년 수준으로 해결 할 수 있다.

$\triangle{ABM}\equiv\triangle{ACM}$ (SSS 합동)
$\because \;\overline{AB}=\overline{AC}$, $\overline{BM}=\overline{CM}$, $\overline{AM}\text{ : 공통}$

$\therefore\; \angle{ABM}=\angle{ACM}$

Q.E.D.

이등변삼각형의 조건 증명

2.두 밑각의 크기가 같으면 이등변 삼각형 이다.

이등변삼각형의 조건 증명

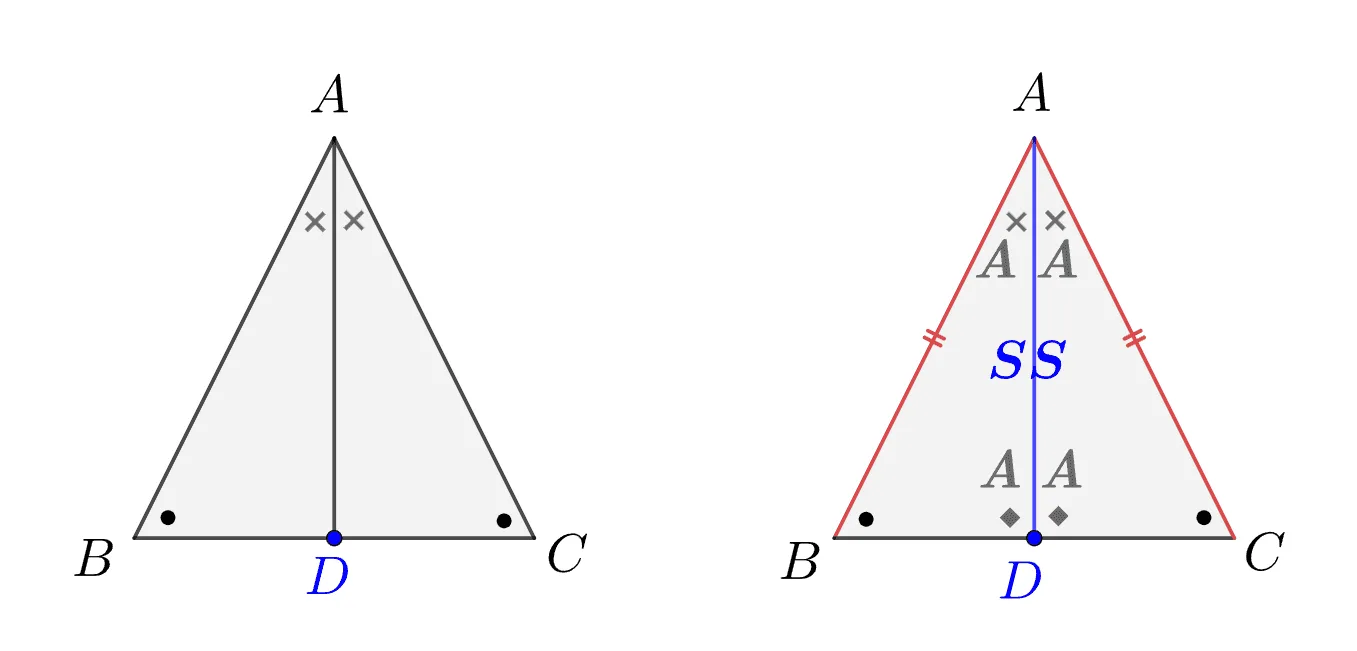
[증명]

증명의 핵심은 $\angle{A}$의 이등분선과 $\overline{BC}$의 교점 $D$에 대하여 보조선 $\overline{AD}$를 그리는 것이다. 이 후 과정은 중학교 1학년 수준에서 해결 가능하다.

$\triangle{ABM}\equiv\triangle{ACM}$ (ASA 합동)
$(\because\; \angle{BAD}=\angle{CAD}$, $\angle{ADB}=\angle{ADC}$, $\overline{AD}\text{ : 공통})$

$\therefore \; \overline{AB}=\overline{AC}$

Q.E.D.

위의 증명에서 $\triangle{ABM}\equiv\triangle{ACM}$ 이므로$\angle{ADB}=\angle{ADC}=90^\circ$, $\overline{BD}=\overline{CD}$이고 이는 다음을 의미한다.

  • $\angle{A}$의 이등분선이 $\overline{BC}$를 수직이등분 한다.

맺음말

삼각형의 합동 조건과 이등변삼각형의 성질을 증명하는 과정을 통해 기하학의 논리적 사고를 깊이 이해할 수 있는 시간이 되었길 바랍니다. 수학적 지식은 처음부터 완벽하게 배우기 어려운 만큼, 학습 과정에서 부족한 논리를 증명을 통해 보완하는 자세를 가지는 것이 중요합니다. 이러한 과정은 수학적 사고력을 키우고, 더욱 엄밀한 수학적 이해를 돕는 데 큰 도움이 될 것입니다.

중학교 1학년 목차

전체 목차 (홈페이지)