이번 시간에는 반비례에 대하여 정리해 보려고 한다. 반비례의 예시를 통해 반비례의 정의 성질 관계식에 대하여 정리하고, 반비례 그래프를 그리고 그래프의 성질에 대해 정리해 보기로 합시다.
목차
반비례 예시
반비례에 대하여 수학적으로 정리하기 전 먼저 다음의 예시를 통해 두 변수 $(x,y)$사의의 관계에 대해 살펴보자.
- 넓이가 60인 직사각형의 가로($x$)의 길이와 세로 ($y$)의 길이 사이 관계
$\begin{align} x=&\;\;1\quad \quad 2\;\;\;\quad 3\quad \; \quad 4\quad \quad\;\; 5 \quad \cdots\\[1em]
y=&\;60 \quad\; 30\quad\;\; 20\quad \;\;\;15\quad\;\;\; 12\; \;\;\cdots \\[1em]\end{align}$
넓이가 일정한 직사각형의 가로의 길이($x$)와 세로의 길이($y$) 사이의 관계를 정리하면 다음과 같은 결과를 얻을 수 있다.
$\begin{align} x\times y&=1\times60=2\times30=3\times20\\[1em]
&=4\times15=5\times12=60\end{align}$
$x\times y=\begin{cases}1\times60\xrightarrow[\;x:\;2\text{배}\;]{\;y:\;\dfrac{1}{2}\text{배}\;}2\times30\\[1em]
1\times60\xrightarrow[\;x:\;3\text{배}\;]{\;y:\;\dfrac{1}{3}\text{배}\;}3\times20\\[1em]
\quad \cdots \end{cases}$
위의 결과를 통해 두 변수 $x,\;y$사이의 관계를 정리해 보면 다음과 같다.
- $x$값이 $2$배, $3$배, $4$배 $\cdots$ 이면
$y$값은 $\dfrac{1}{2}$배, $\dfrac{1}{3}$배, $\dfrac{1}{4}$배 $\cdots$ 가 되는 관계
위와 같은 성질을 만족하는 두 변수 사이의 관계를 반비례 관계라고 한다.
반비례의 정의와 성질
반비례의 정의
두 변수 $x$, $y$에 대하여 다음과 같은 성질을 만족하는 관계를 ‘반비례’라고 한다.
- $x$값이 $2$배, $3$배, $4$배 $\cdots$ 이면
$y$값은 $\dfrac{1}{2}$배, $\dfrac{1}{3}$배, $\dfrac{1}{4}$배 $\cdots$ 가 되는 관계
반비례 관계는 $x(\neq0)$값에 따라 $y$값이 오직 하나($\bbox[#94feff]{x\text{값의 역수}}$)로 결정되기 때문에 $\bbox[#ffff00]{\text{함수}}$이다.
반비례의 성질
- 두 변수의 곱이 일정하다.
$\bbox[#ffff00]{x\text{값}}$이 $2$배, $3$배, $4$배 $\cdots\ \bbox[#ffc5fd]{\square}$배 됨에 따라 $\bbox[#dcff8c]{y\text{값}}$은 $\dfrac{1}{2}$배, $\dfrac{1}{3}$배, $\dfrac{1}{4}$배 $\cdots\ \bbox[#ffc5fd]{\dfrac{1}{\square}}$배 가 된다 따라서 두 변수의 곱을 정리하면 일정함을 알 수 있다.
$\bbox[#dcff8c]{x}\times \bbox[#ffff00]{y}\;\xrightarrow[y\text{값}:\;\dfrac{1}{\square}\text{배}\;]{x\text{값}:\;\square\text{배}} \bbox[#dcff8c]{x \times \square} \times \bbox[#ffff00]{y\times \dfrac{1}{\square}} = \bbox[#ffff00]{x} \times \bbox[#dcff8c]{y}$
$\therefore \; \bbox[#ffff00]{x\text{값}}\times \bbox[#dcff8c]{y\text{값}}= \text{일정}\\[1em]$
반비례 관계식
예로 들었던 상황을 관계식으로 정리하면 다음과 같다.
- 넓이가 60인 직사각형의 가로($x$)의 길이와 세로 ($y$)의 길이 사이 관계
- $x\times y=60\xrightarrow[\text{양변}\;\div x]{\text{등식의 성질}} y=\dfrac{60}{x}$
반비례 일반형 관계식
$x\times y$의 값이 일정하고, 일정한 값(상수)을 $a(\neq0)$로 두면 다음과 같이 표현 할 수 있다.
- $x\times y= a \; ,(\text{단}, a\neq0)$
- $\therefore \; y=\dfrac{a}{x}\;(\text{단}, \;a\neq0)$
여기서$a(\neq0)$조건은 $x,\;y$가 0이 될 수 없음을 알려 준다. $x\neq0$이므로 등식의 양변을 $x$나누어 정리할 수 있고, 반비례의 일반형 관계식을 얻을 수 있다.
이제 반비례 관계의 그래프에 대하여 정리해 보기로 하자.
반비례 그래프
반비례 관계식 $y=\dfrac{a}{x}\;(\text{단}, \;a\neq0)$의 그래프에 대해 학습해 보자.
$y=\dfrac{a}{x}\;(a>0)$ 그래프
$y=\dfrac{a}{x}\;(a>0)$의 그래프를 $y=\dfrac{1}{x},\; y=\dfrac{2}{x},\;y=\dfrac{1}{2x}$를 이용해 정리해 보자.
- 참고사항 $y=\dfrac{1}{2x}$은 반비례 이다.
- $y=\dfrac{a}{x}\xrightarrow[]{a=\dfrac{1}{2}} y= a \times \dfrac{1}{x}=\dfrac{1}{2x}$
1단계: 대응표 그리기
$y=\dfrac{1}{x},\; y=\dfrac{2}{x},\;y=\dfrac{1}{2x}$ 관계식을 이용해 대응표 만들면 아래와 같다. 연산에 취약한 학생은 $x$ 값을 대입하여 계산하면서 나눗셈의 생략 표현과 역수를 이용한 계산을 연습하길 바란다.
$\begin{align}y=\dfrac{a}{x} &\xrightarrow[]{\div \text{부활}} y=a \div x\\[1em]
&\xrightarrow[]{\div \rightarrow \text{역수의 곱}} y=a \times (x\text{의 역수})\end{align}$
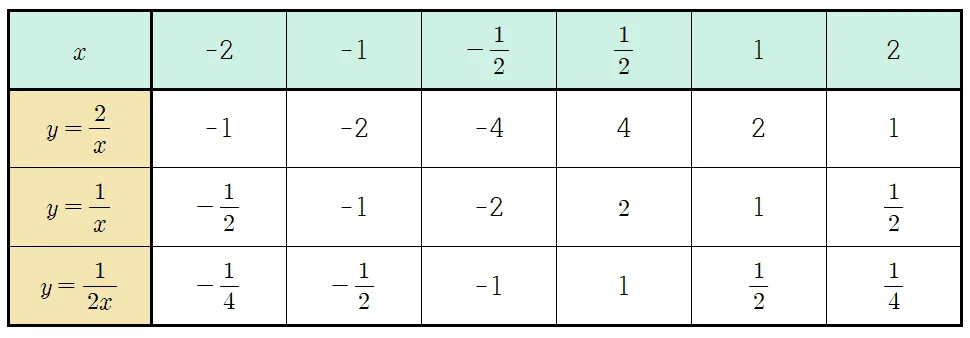
2단계: 순서쌍 만들기
대응표를 이용해 $(x,y)$의 순서쌍을 만든다.
3단계: 점찍기
대응표의 순서쌍을 이용해 점을 찍고, $x$값을 확장하여 정수와 유리수를 전체를 고려하면 대응표에 주어진 $x$값들 사이에도 무수히 많은 $x$값을 추가할 수 있다. 유리수까지 고려하여 점을 찍으면 그래프는 아래와 같은 곡선이 됨을 알 수 있다.
사실 수직선위에는 유리수만 있는 것이 아니다. 수직선위에 유리수가 아닌 무리수에 대해서도 생각해야 한다. 부족한 부분은 나중에 수를 확장하면서 자연스럽게 확장하여 생각하기로 하자.
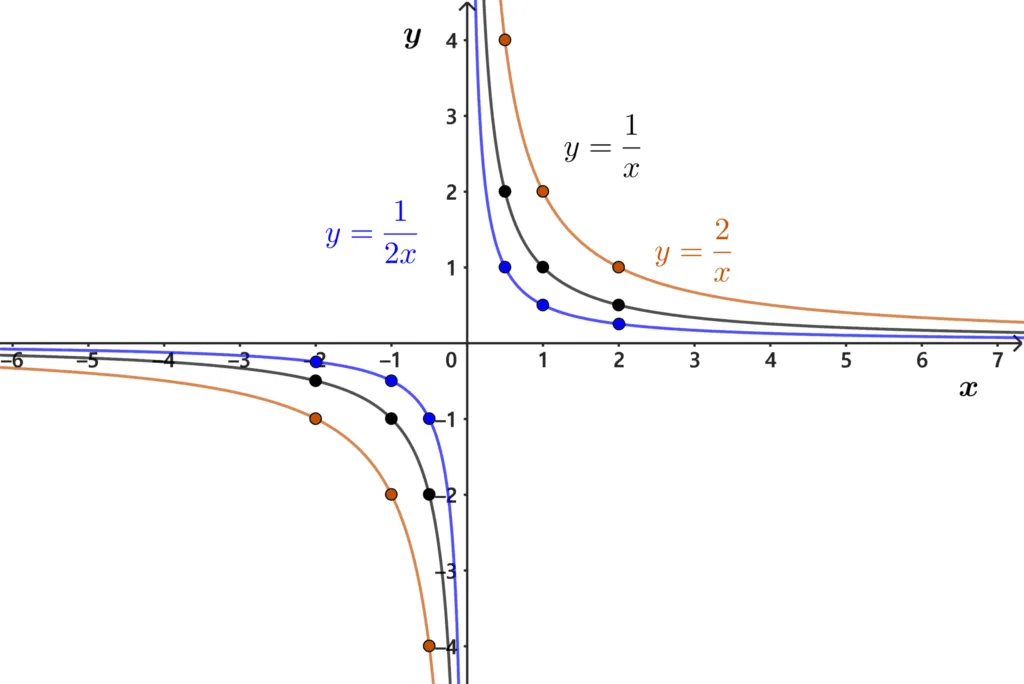
$y=\dfrac{a}{x}\;(a<0)$ 그래프
이번에는 $y=\dfrac{a}{x}\;(a>0)$ 그래프를 그려보기로 하자. $a>0$인 그래프를 그리는 과정과 일치하므로 대응표와 그래프만 제시하도록 하겠다. 대응표를 채우고 좌표평면에 점을 찍어보는 과정을 꼭 개인적으로 수행하고 넘어가길 바란다.
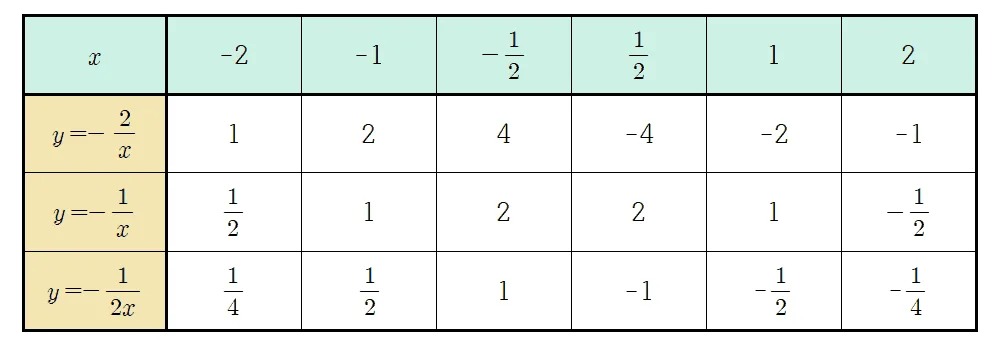
대응표를 이용해 순서쌍에 점을 찍고 $x$값을 유리수 전체로 확장하면 다음과 같은 그래프를 얻을 수 있다.
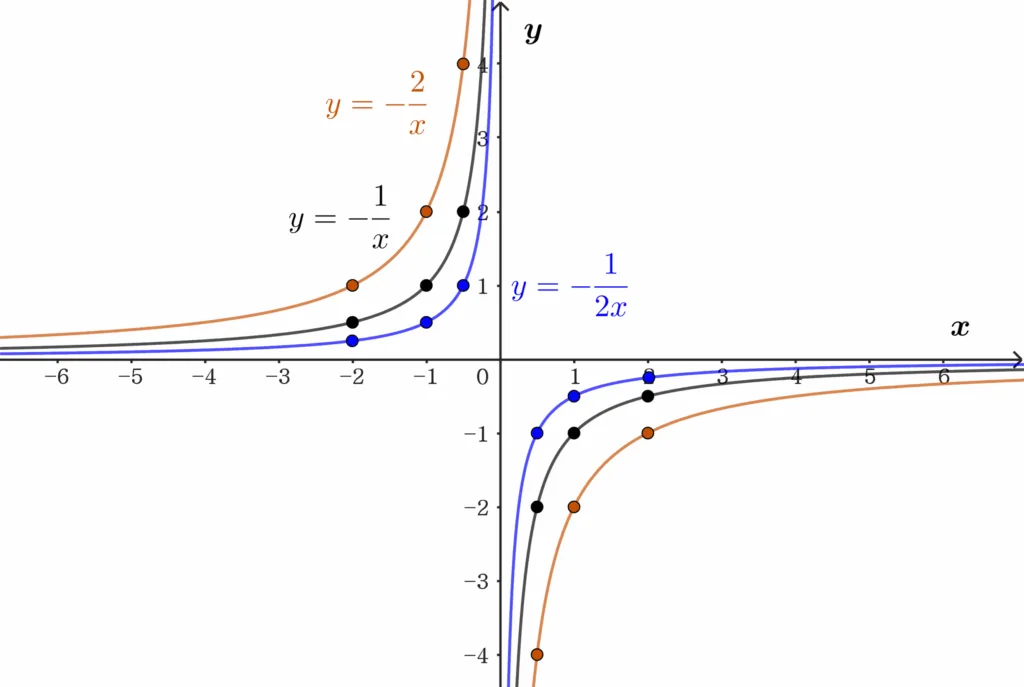
이제 반비례 $x\times y= a \; ,(a\neq0)$의 그래프의 성질을 정리해 보자.
$y=\dfrac{a}{x}$그래프 성질
$a$의 부호에 따라 그래프의 성질을 정리하면 다음과 같다.
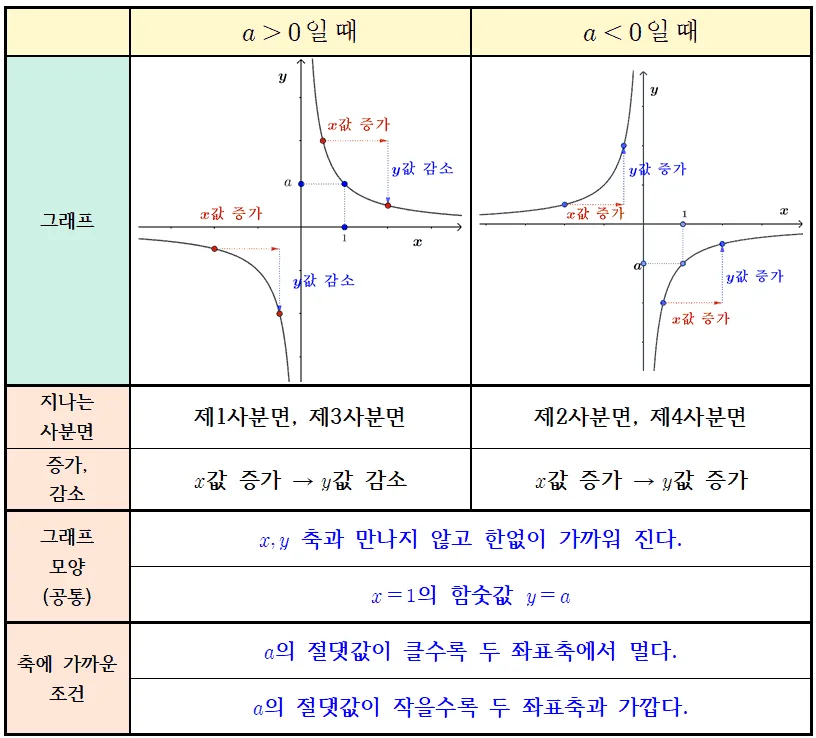
반비례 그래프의 공통성질
$y=\dfrac{a}{x}$의 그래프는 $a$의 부호에 관계없이 다음과 같은 성질을 갖는다.
- $x,\;y$축과 마나지 않으면서 한없이 가까워진다
- $x=1$에서 함숫값 $y=a$이다.
- $a$의 절댓값이 클 수록 좌표축에서 멀어진다.
- $a$의 절댓값이 적을 수록 좌표축과 가까워진다.
정리
반비례의 정의
- $x$값이 $2$배, $3$배, $4$배 $\cdots$ 이면
$y$값은 $\dfrac{1}{2}$배, $\dfrac{1}{3}$배, $\dfrac{1}{4}$배 $\cdots$ 가 되는 관계
반비레의 성질
- $x\times y=a(\text{상수, 일정})$
반비례 관계식
- $y=\dfrac{a}{x}\;(\text{단}, \;a\neq0)$
이상으로 반비례에 대한 학습을 마무리 하도록 하겠다.
