이 글에서는 삼각형과 다각형의 내각 외각 문제를 유형별로 정리 하였습니다. 앞으로 수학학습 과정에 의미 있는 문제를 위주로 다루었으니 이해하고 넘어가길 바랍니다.
목차
삼각형 내각 외각 성질 문제
$\triangle{ABC}$의 내각과 외각의 성질은 다음과 같다.
- $a+b+c=180^\circ$
- $(A\text{의 외각})=b+c$
첫 번째 성질을 변형하여 다음의 성질을 추가로 정리해 두자.
- $\dfrac{a}{2}+\dfrac{b}{2}+\dfrac{c}{2}=90^\circ$
화살촉 모양
[문제] 주어진 화살촉 모양의 도형에서 $x$의 크기를 $a,\;b,\;c$를 이용해 나타내라.
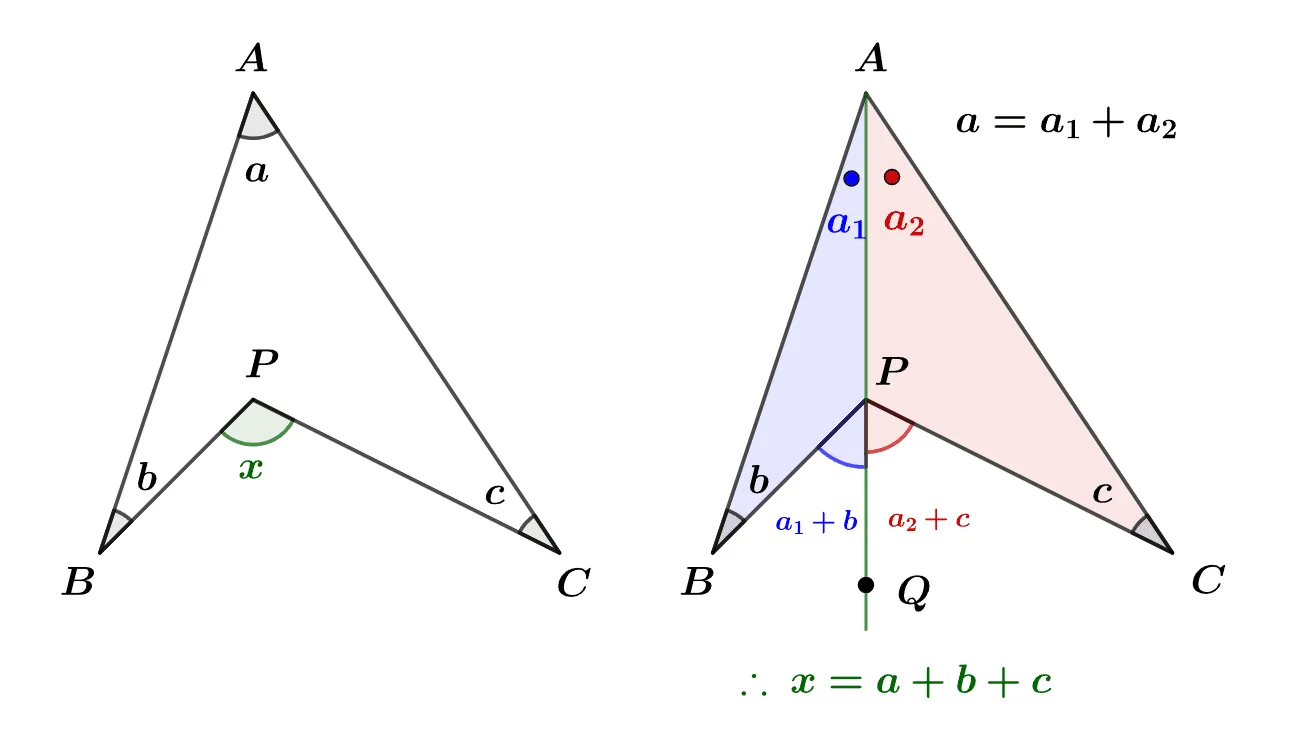
[풀이]
$\overline{AP}$에 의해 나누어진 $\bbox[#ffff00]{\angle{a}}$의 각을 각각 $\bbox[#ffff00]{a_1},\; \bbox[#ffff00]{a_2}$라고 두고, $\overline{AP}$의 연장선 위의 점을 Q라고 할 때
$\angle{BPQ}=\bbox[#ffff00]{a_1}+b$, $\angle{CPQ}=\bbox[#ffff00]{a_2}+c$
$\therefore\; x=\bbox[#ffff00]{a_1}+\bbox[#ffff00]{a_2}+b+c=\bbox[#ffff00]{a}+b+c$
화살촉 유형
[문제] 아래의 도형에서 $a+b+c+d+e+f+g$의 값을 구하여라.
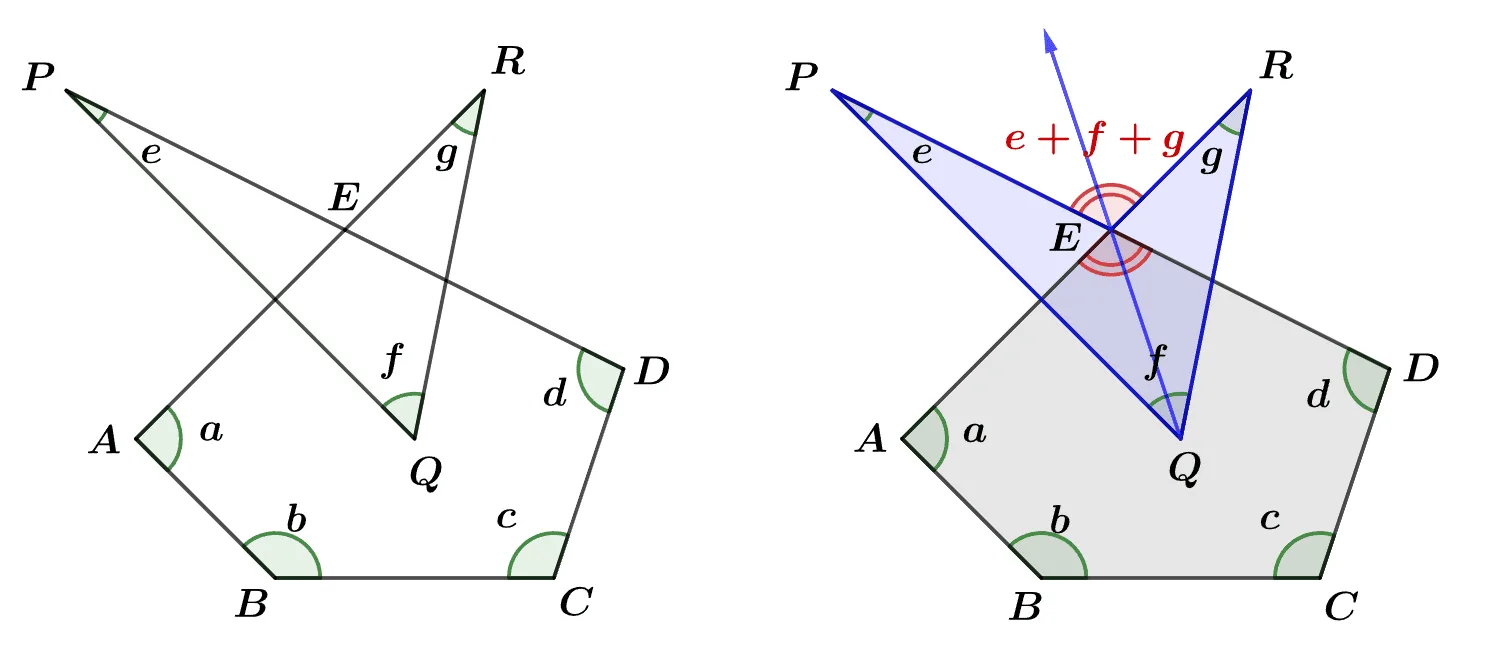
[풀이]
화살촉 모양의 다각형에서 $\overrightarrow{QE}$를 그으면 삼각형의 외각의 성질에 의해 $\angle{PER}=e+f+g$이다.
맞꼭지각의 성질에 의해 $\angle{PER}=\angle{AED}=e+f+g$이므로 $a+b+c+d+e+f+g$는 오각형의 내각의 크기의 합이다.
$\therefore\; 180^\circ \times (5-2)=540^\circ$
삼각형의 각의 이등분선
내심과 관련된 문제 유형
[문제] $\triangle{ABC}$의 두 내각 $\angle{A},\; \angle{C}$을 이등분하는 직선이 만나는 교점$I$에 대하여 $\angle{AIC}$를 $\angle{B}=b$로 나타내어라.
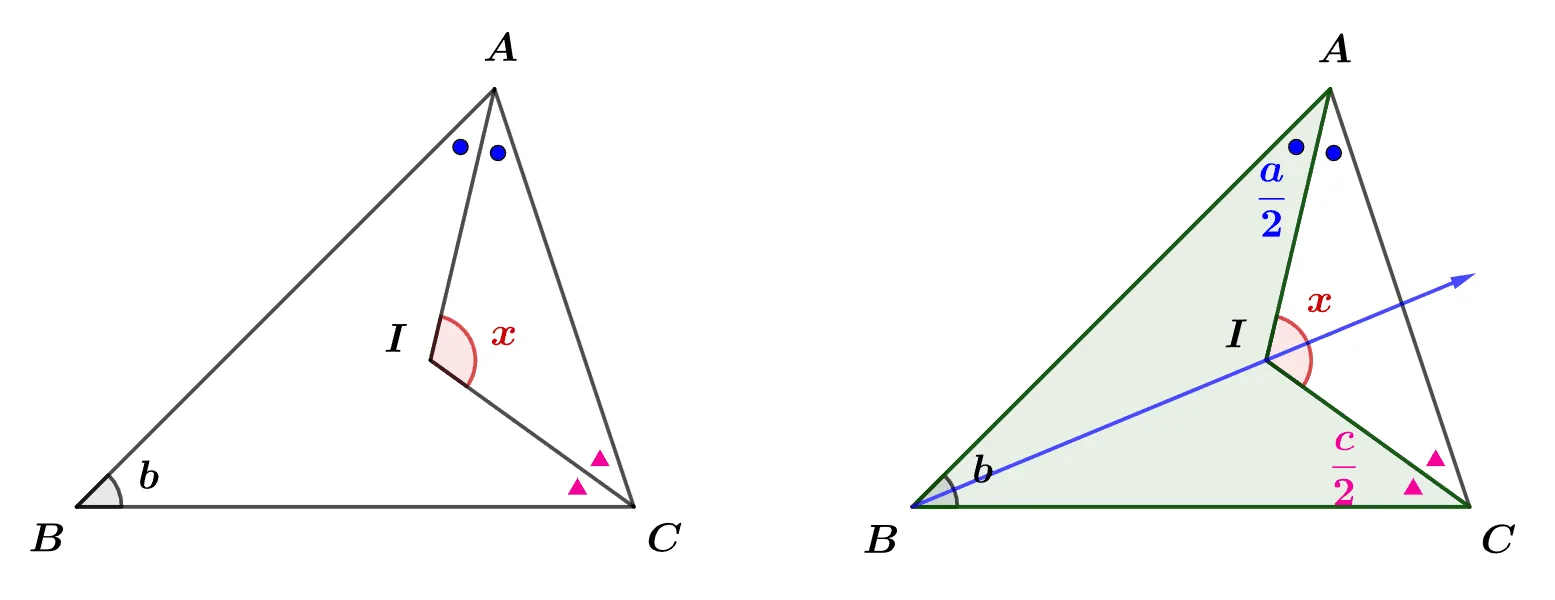
삼각형 내부에 점 $I$가 있어 화살촉 모양의 도형을 이용할 수 있다.
다각형 $ABCI$의 $\overrightarrow{BI}$에 대하여 삼각형의 외각의 성질을 적용하면
$x=b+\dfrac{a}{2}+\dfrac{c}{2}\\[1em]$이고
$\dfrac{a}{2}+\dfrac{b}{2}+\dfrac{c}{2}=90^\circ$이므로
$\therefore\; x=90^\circ+\dfrac{b}{2}$
삼각형$\triangle{ABC}$의 내부의 점$P$가 주어질 때 화살촉 모양의 도형이 만들어 지고 이를 이용해 각을 구할 수 있음을 기억하자.
방심과 관련된 문제 유형
[문제1] $\triangle{ABC}$의 두 변의 연장선 위의 점 $P,\;Q$와 각 $\angle{CAQ}$와 $\angle{ACP}$의 이등분선의 교점 $E$에 대하여 $\angle{AEC}$의 크기를 $a,\;c$를 이용해 나타내어라.
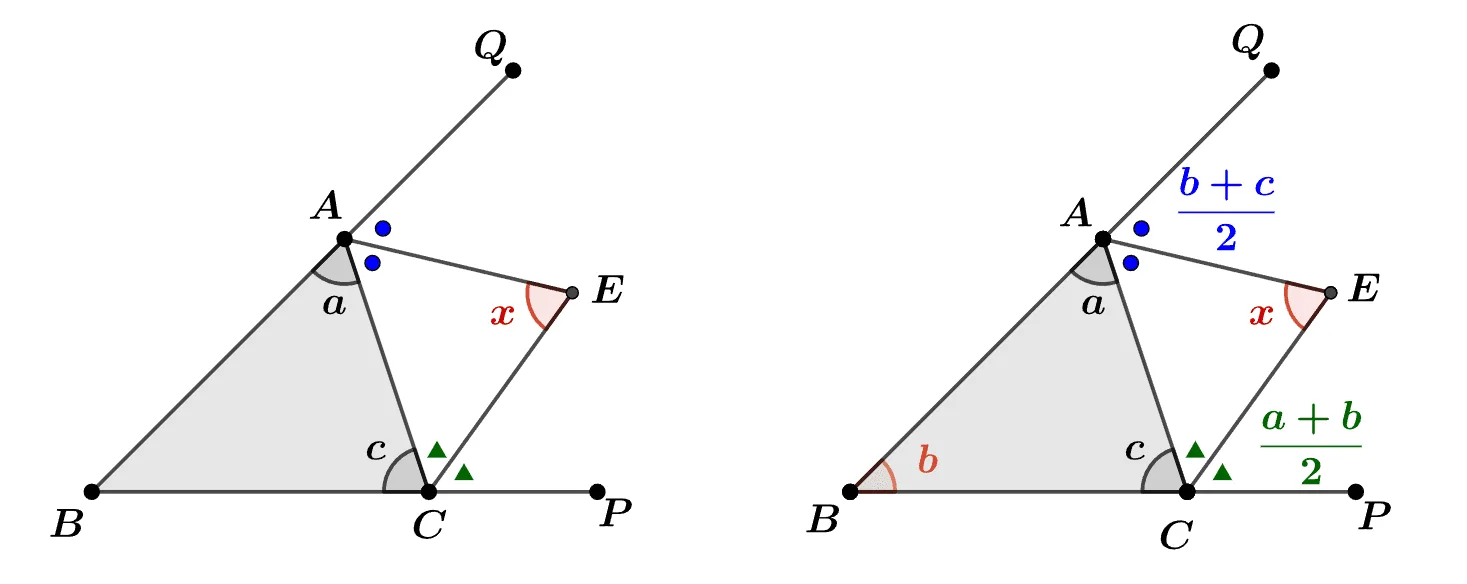
$\angle{B}=b$로 두면 삼각형 외각의 성질에 의해
$\angle{CAQ}=b+c$, $\angle{ACP}=a+b\\[1em]$이고
$\angle{CAE}=\dfrac{b+c}{2}$, $\angle{ACE}=\dfrac{a+b}{2}\\[1em]$이며, $\dfrac{b+c}{2}+\dfrac{a+b}{2}+x=180^\circ$이다.
좌변을 고려하여 $180^\circ=a+b+c$ 로 두면
$\begin{align}\dfrac{b+c}{2}&+\dfrac{a+b}{2}+x=a+b+c\\[2em]
x&=a+b+c-\dfrac{b+c}{2}-\dfrac{a+b}{2}\\[2em]
\therefore \;x&=\dfrac{a}{2}+\dfrac{c}{2}\end{align}$
[문제2] $\triangle{ABC}$의 변 $\overline{BC}$의 연장선 상의 점 $P$와 $\angle{ABC}\;\angle{ACP}$를 이등분하는 두 직선의 교점 $E$에 대하여 $\angle{BEC}$의 크기를 $a$를 이용해 나타내어라.
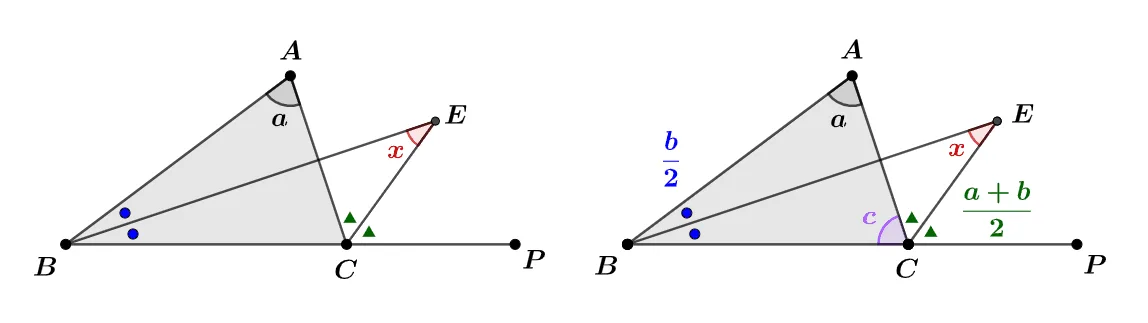
[풀이]
$\angle{ABC}=b,\;\angle{ACB}=c$로 두면
$\angle{EBC}=\dfrac{b}{2},\; \angle{ECB}={\color{#b477f0}c}+{\color{#246b25}\dfrac{a+b}{2}}$이다.
$\triangle{EBC}$에 대하여 $\dfrac{b}{2}+{\color{#b477f0}c}+{\color{#246b25}\dfrac{a+b}{2}}+x=180^\circ$이다.
좌변을 고려하여 $180^\circ=a+b+c$로 두면
$\begin{align}\dfrac{b}{2}+&c+\dfrac{a+b}{2}+x=a+b+c\\[2em]
x&=a+b+c-\dfrac{b}{2}-c-\dfrac{a+b}{2}\\[2em]
\therefore\;x&=\dfrac{a}{2}\end{align}$
나비 모양 도형
[예제] 주어진 도형 에서 $x+y=z+w$ 이 성립함을 보여라.
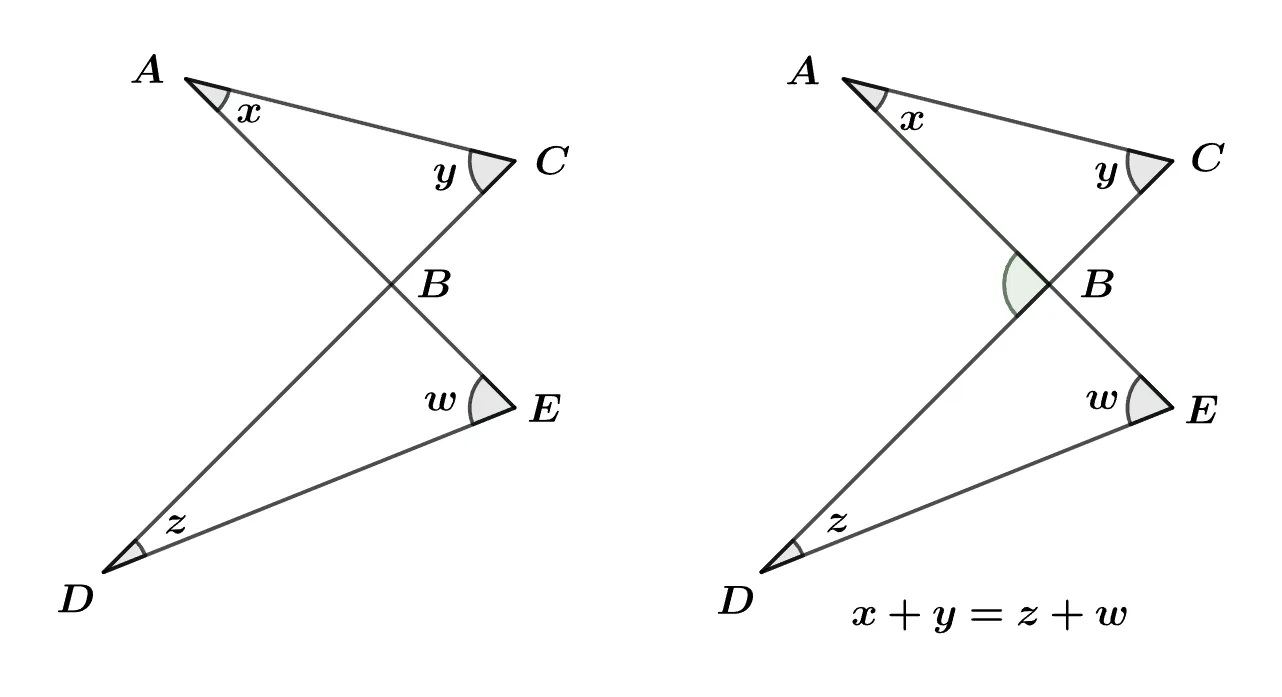
[풀이] 삼각형 외각의 성질에 의해
$\triangle{ABC}$의 외각 $\angle{ABD}=x+y$ 이고,
$\triangle{BDE}$의 외각 $\angle{ABD}=z+w$ 이다.
따라서 $x+y=z+w$ 이다.
문제 유형
[문제1] 주어진 도형에 대하여 $a+b+c+d+e+f+g+h$값을 구하여라.
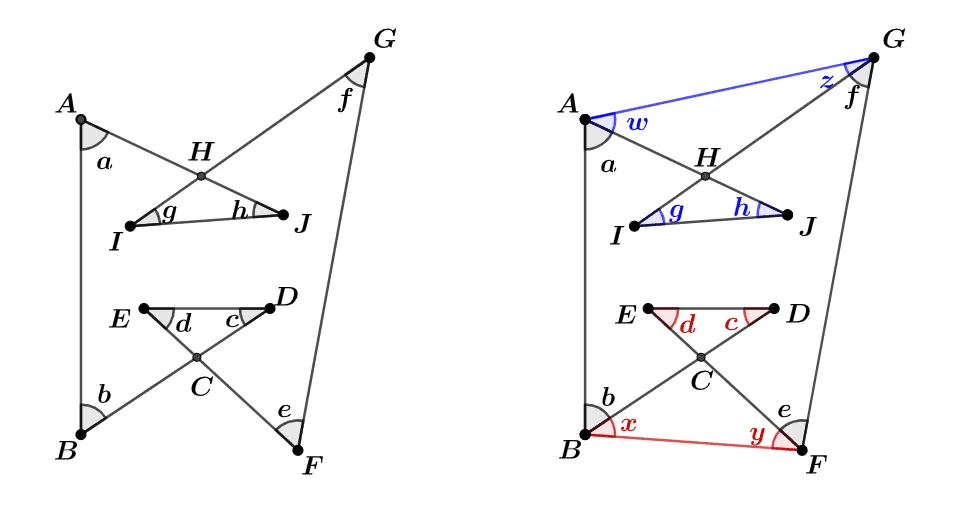
삼각형 외각의 성질에 의해
$\bbox[#ffff00]{c+d}=\bbox[#ffff00]{x+y}$, $\bbox[#dcff8c]{g+h}=\bbox[#dcff8c]{w+z}$ 이고 따라서
$\begin{align}a+&b+\bbox[#ffff00]{c+d}+e+f+\bbox[#dcff8c]{g+h}\\[1em]
&=a+b+\bbox[#ffff00]{x+y}+e+f+\bbox[#dcff8c]{w+z}\\[1em]
&=360^\circ\end{align}$
[문제2] 주어진 도형에 대하여 $a+b+c+d+e+f+g+h+i+j$값을 구하여라.
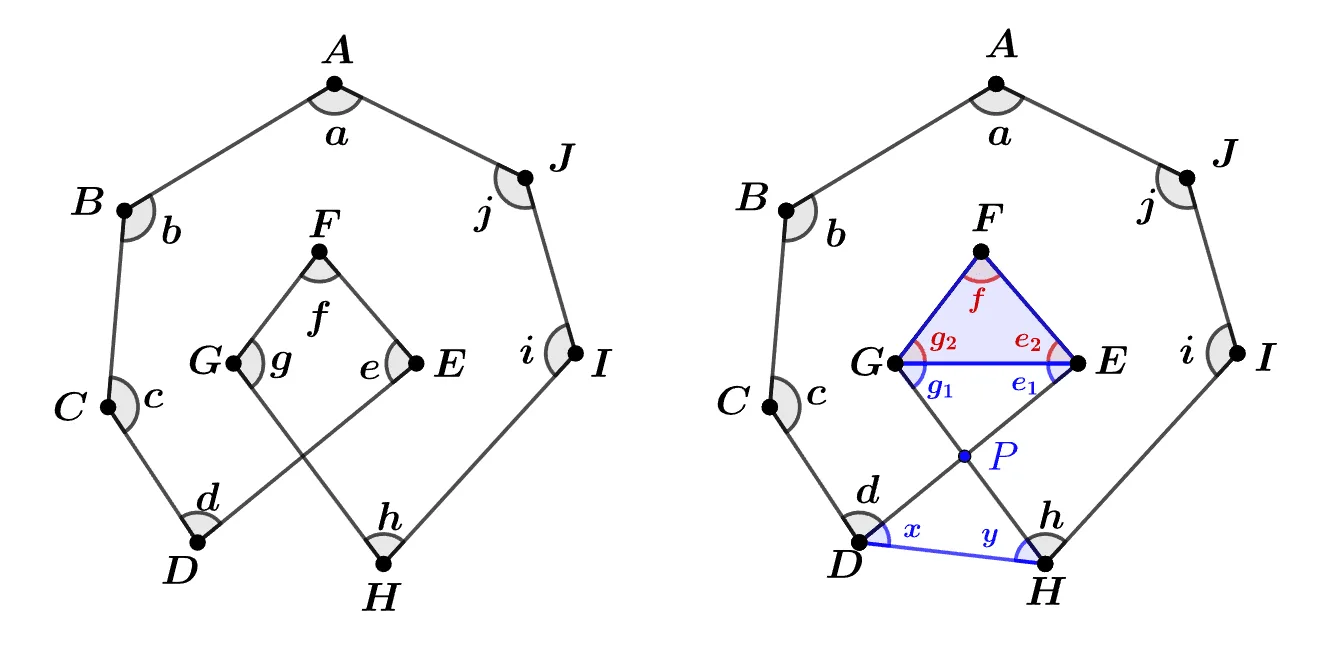
[풀이]
보조선 $\overline{DH}$, $\overline{GE}$을 그린다.
- $\overline{DH}$ : 다각형의 내각의 합을 이용하기 위한 보조선
- $\overline{GE}$ : 각을 옮겨 계산하기 위한 보조선
점 ${\color{blue}P}$를 중심으로 나비 모양의 도형에서 다음이 성립한다.
${\color{blue}g_1}+{\color{blue}e_1}={\color{blue}x}+{\color{blue}y}$
위의 사실을 이용해 주어진 식을 정리하면
$\begin{align}&a+b+c+d+e+f+g+h+i+j\\[1em]
&=\begin{pmatrix}a+b+c+d+({\color{blue}e_1}+e_2)\\[1em]
+f+({\color{blue}g_1}+g_2)+h+i+j\end{pmatrix}\\[1em]
&=\begin{pmatrix}\bbox[#ffff00]{a+b+c+d+{\color{blue}x+y}+h+i+j}\\[1em]
+\bbox[#dcff8c]{e_2+f+g_2}\end{pmatrix}\\[1em]
&=\bbox[#ffff00]{\text{7각형의 내각의 합}}+\bbox[#dcff8c]{\text{삼각형의 내각의 합}}\\[1em]
&=\bbox[#ffff00]{180^\circ\times(7-2)}+\bbox[#dcff8c]{180^\circ}\end{align}$
$\therefore\; (\text{준식})=1080^\circ$
다각형 내각 외각 문제
오각성 문제
[문제] 주어진 오각성에 대하여 $a+b+c+d+e$의 값을 구하여라.
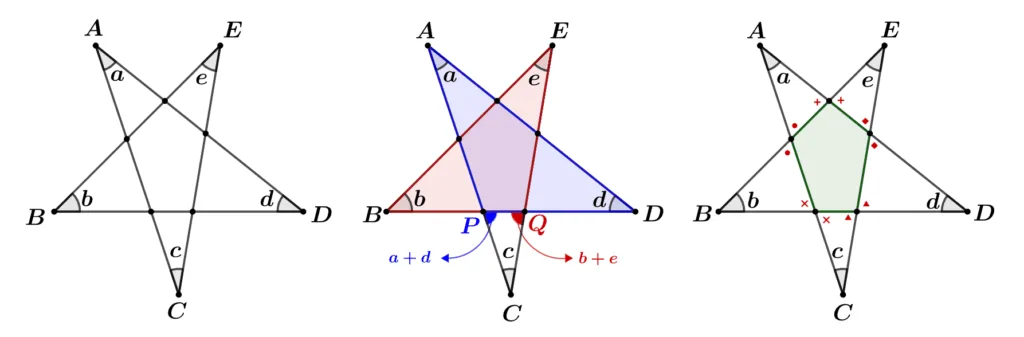
[풀이1]
$\triangle{APD},\;\triangle{EBQ}$에 대하여 외각의 성질을 적용하면 $\color{blue}\angle{CPQ}=a+d$, $\color{red}\angle{PQC}=b+e$이고
$\begin{align}{\color{blue}a}&+{\color{red}b}+c+{\color{blue}d}+{\color{red}e}\\[1em]
&=\triangle{PQC} \text{의 내각의 합}\\[1em]
&=180^\circ\end{align}$
[풀이2]
5개 삼각형의 내각을 오각형의 외각을 이용해 모두 더하면 다음과 같다.
$\begin{align} \begin{pmatrix}\bbox[#ffff00]{a+b+c+d+e}\\[1em]
+{\color{red}2}\times({\color{red}\circ}+{\color{red}\bullet}+{\color{red}\times}+{\color{red}\blacktriangle}+{\color{red}\blacklozenge})\end{pmatrix}\\[1em]
=\begin{pmatrix}\bbox[#ffff00]{a+b+c+d+e}\\[1em]
+{\color{red}2}\times {\color{red}\text{오각형 외각의 합}}\end{pmatrix}\\[1em]
=\bbox[#ffff00]{a+b+c+d+e}+{\color{red}2}\times {\color{red}360^\circ}\end{align}$
5개 삼각형에서 내각의 합을 모두 더하면 $180^\circ\times 5$ 이므로 다음이 성립한다.
$\bbox[#ffff00]{a+b+c+d+e}+{\color{red}2}\times {\color{red}360^\circ}=180^\circ\times 5$
이항하여 계산하면
$\begin{align}\bbox[#ffff00]{a+b+c+d+e}&=180^\circ(5-{\color{red}4})\\[1em]
&=180^\circ\end{align}$
칠각성 문제
[문제] 주어진 칠각성에 대하여 $a+b+c+d+e+f+g$의 값을 구하여라.
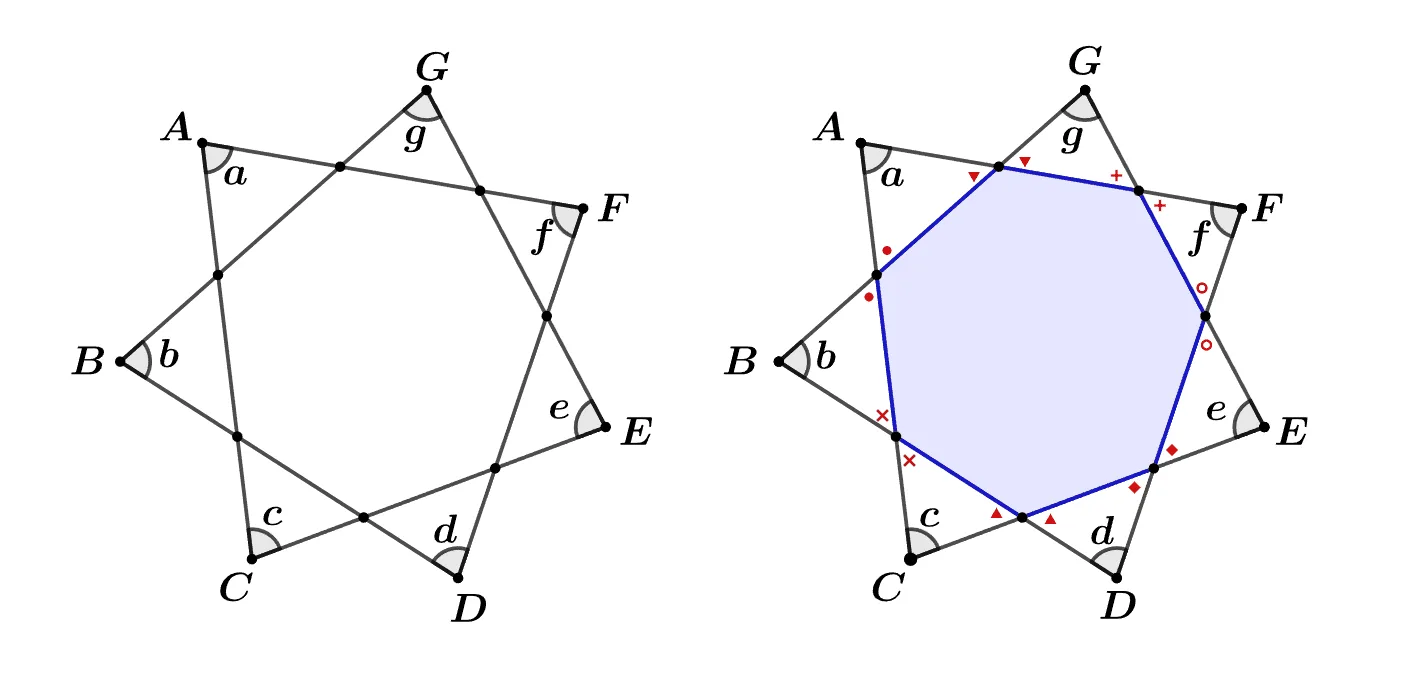
[풀이}
7개 삼각형의 내각을 칠각형의 외각을 이용해 모두 더하면 다음과 같다.
$\begin{pmatrix} a+b+c+d+e+f+g\\[1em]
+{\color{red}2}\times {\color{red}\text{칠각형 외각의 합}}\end{pmatrix}\\[2em]$
$=a+b+c+d+e+f+g+{\color{red}2}\times {\color{red}360^\circ}$
7개 삼각형의 내각을 모두 더한 값은 $180^\circ\times 7$이므로
$\begin{pmatrix}\bbox[#ffff00]{a+b+c+d+e+f+g}\\[1em]+{\color{red}2}\times {\color{red}360^\circ}\end{pmatrix}
=180^\circ\times 7$
이항하여 계산하면
$\begin{align} &\bbox[#ffff00]{a+b+c+d+e+f+g}\\[1em]
&\quad=180^\circ\times(7-{\color{red}4})\\[1em]
&\quad=540^\circ\end{align}$
이상으로 다각형과 삼각형의 내각과 외각의 성질에 관련된 문제풀이를 마무리 하도록 하겠습니다. 다양한 문제를 참고서를 이용해 풀어보시길 바랍니다.
