다면체와 정다면체 문제

이 글에서는 다면체와 정다면체와 관련된 문제를 다루었습니다. 정다면체를 변형시킨 쌍대 다면체, 준정다면체, 깎은 정다면체와 관련된 문제와 전개도를 활용한 다양한 문제에 대한 내용을 포함하고 있습니다.

다면체 문제

[문제] 다음 조건을 모두 만족하는 입체도형의 면, 모서리, 꼭짓점 개수를 구하여라.

• 두 밑면은 서로 평행하다.
• 옆면의 모양은 사다리꼴이다.
• 밑면의 모양은 구각형이다.

[풀이] 주어진 조건을 만족하는 입체도형은 구각뿔대이다.

• 면 : 9+2=11
• 모서리 : 9+9+9=27
• 꼭짓점 : 9+9=18

[문제] 다음 조건을 만족시키는 입체도형의 꼭짓점 개수를 구하여라.

• 밑면이 하나이다.
• 옆면이 삼각형이다.
• 모서리와 꼭짓점의 개수를 더하면 25이다.

[풀이] 주어진 조건을 만족하는 입체도형은 $n$각뿔이다.

• $n$각뿔의 모서리 개수 : $n+n=2n$
• $n$각뿔의 꼭짓점 개수 : $n+1$

$2n+n+1=3n+1=25$
$n=8$이고 8각뿔의 꼭짓점 개수는 9개이다.

정다면체 문제

정다면체의 정의

[문제] 정다면체에 대한 설명 중 바르지 않은 것을 찾아 고치시오.

1. 각 면의 모양이 모두 합동인 정다각형이다.
2. 자연수 n에 대하여 정n각형으로 정다면체를 만들 수 있을 때, 가능한 n의 값은 5개이다.
3. 각 꼭짓점에 모인 면의 개수는 일정하다.
4. 정삼각형으로 만들 수 있는 정다면체는 하나이다.
5. 정다면체는 오직 5개 뿐이다.
6. 모든 정다면체는 평행한 면이 있다.
7. 정다면체의 면의 개수보다 꼭짓점의 개수가 더 많다.
8. 정다면체의 모서리 개수는 면, 꼭짓점 개수 보다 항상 많다.

[풀이] 1,3,5,8은 참이다.

2. 정삼각형, 정사각형, 정오각형만 정다면체를 만들수 있다. 따라서 자연수 n은 3개이다.

4. 정삼각형으로 만들 수 있는 정다면체는 정사면체, 정팔면체, 정이십면체 세 개이다.

6. 정사면체는 평행한 면이 없다.

7. 정팔면체는 꼭짓점(6개)보다 면(8개)의 수가 더 많다.

면 모서리 꼭짓점 개수

(볼록) 다면체의 면 하나에 적어도 $3$개의 모서리가 있고 모서리는 $2$개의 면이 만날 때 생긴다. 따라서 주어진 다면체의 최소 모서리 개수를 다음과 같이 생각할 수 있다.

$$\begin{array}{rl}{\displaystyle \frac{3\times \text{(면의 개수)}}{2}}& \le \text{(모서리 개수)}\\ {\displaystyle \frac{3}{2}}\times \text{(면의 개수)}& \le \text{(모서리 개수)}\\ \therefore \text{(모서리 개수)}& >\text{(면의 개수)}\end{array}$$

오일러 정리($v-e+f=2$)를 이용해 꼭짓점의 개수와 모서리의 개수를 비교하면

$$\begin{array}{rl}v& =e-f+2(f\ge 3)\\ v& =e-f+2\le e-1<e\end{array}$$

따라서 볼록 다면체의 모서리의 개수는 항상 면, 꼭짓점 개수보다 많다.

정다면체의 종류

[문제] 정다면체를 구성할 수 있는 조건을 찾고 만들 수 있는 정다면체를 구하여라.

1. 면의 모양이 정삼각형이고, 한 꼭짓점에 2개의 면이 모인다.
2. 면의 모양이 정사각형이고, 한 꼭짓점에 3개의 면이 모인다.
3. 면의 모양이 정삼각형이고, 한 꼭짓점에 4개의 면이 모인다.
4. 면의 모양이 정오각형이고, 한 꼭짓점에 3개의 면이 모인다.
5. 면의 모양이 정삼각형이고, 한 꼭짓점에 5개의 면이 모인다.
6. 면의 모양이 정육각형이고, 한 꼭짓점에 3개의 면이 모인다.

[풀이]

1. 입체도형을 구성하기 위해 한 꼭짓점에 최소 3개의 면이 필요하다.
2. 정육면체
3. 정팔면체
4. 정십이면체
5. 정이십면체
6. 정육각형의 한 내각이 ${120}^{\circ }$이므로 세 면이 모이면 ${360}^{\circ }$가 되고 평면을 만든다.

꼭짓점, 모서리 개수

[문제] 정십이면체와 정이십면체의 꼭짓점과 모서리 개수를 구하는 과정을 서술하여라.

[풀이]

• 정십이면체
  • 꼭짓점: ${\displaystyle \frac{5\times 12}{3}}=20$개
  • 모서리: ${\displaystyle \frac{5\times 12}{2}}=30$개
• 정이십면체
  • 꼭짓점: ${\displaystyle \frac{3\times 20}{5}}=12$개
  • 모서리: ${\displaystyle \frac{3\times 20}{2}}=30$개

풀이에 대한 자세한 설명은 정다면체 포스팅을 참고하길 바란다.

정다면체를 변형한 입체도형 문제

쌍대 다면체

[문제] 주어진 정다면체의 이웃한 면의 중심을 연결한 정다면체를 구해라.

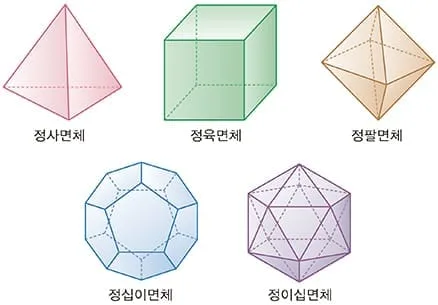
[풀이]

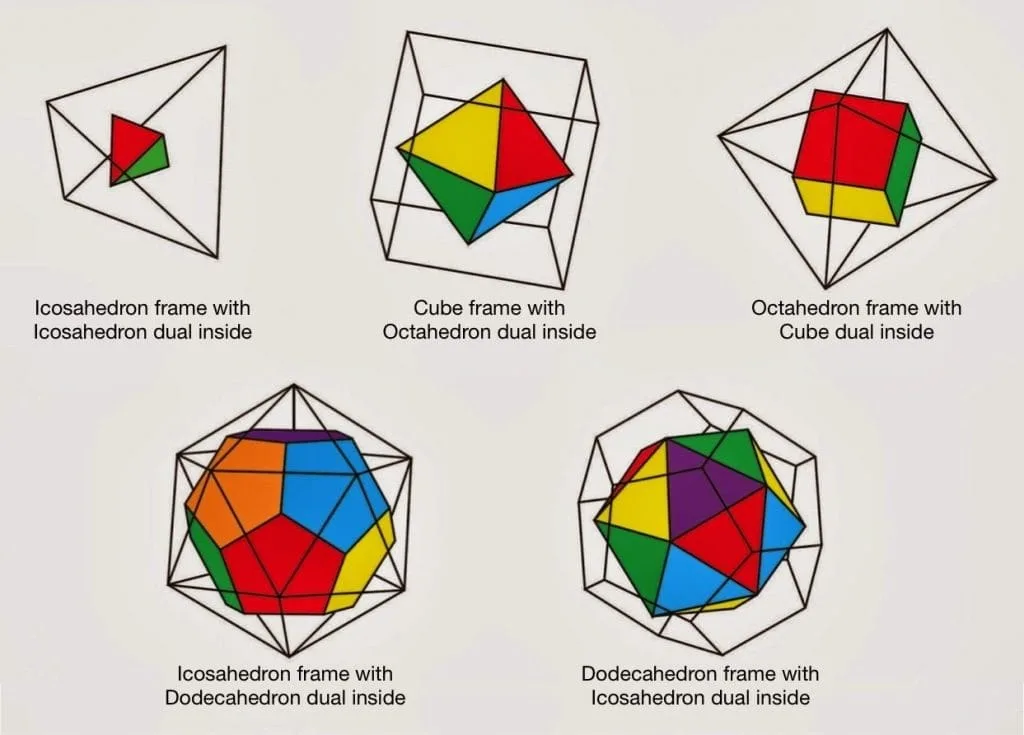
• 정사면체 $\leftrightarrow$ 정사면체
• 정육면체 $\leftrightarrow$ 정팔면체 (순환)
• 정십이면체 $\leftrightarrow$ 정이십면체 (순환)

준정다면체

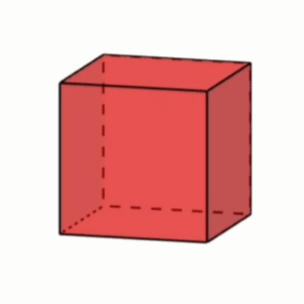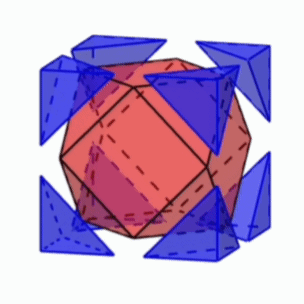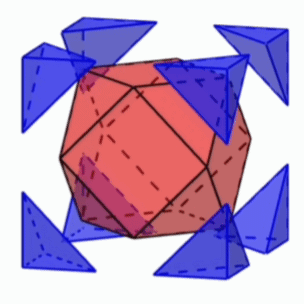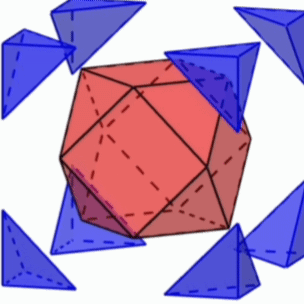
[문제] 정육면체의 모서리절반을 잘라낸 입체도형(육팔면체)에 대하여 다음에 답하여라.

1. 면의 종류와 개수
2. 꼭짓점 개수
3. 모서리 개수

[풀이]

1. 면의 종류 : 정삼각형, 정사각형
   정육면체의 면 $\to$ 정사각형 6개
   꼭짓점이 잘린 곳 $\to$ 정삼각형 8개
2. 꼭짓점 개수
   사각형이 6개 삼각형이 8개 이므로 중복을 허용하여 개수를 세고 중복횟수로 나누어 계산
   $4\times 6+3\times 8=48$$\underset{\text{중복:4}}{\overset{÷4}{\to }}{\displaystyle \frac{48}{4}}=12$개
3. 모서리 개수
4. 사각형이 6개 삼각형이 8개 이므로 중복을 허용하여 개수를 세고 중복횟수로 나누어 계산
   $4\times 6+3\times 8=48$$\underset{\text{중복:2}}{\overset{÷2}{\to }}{\displaystyle \frac{48}{2}}=24$개

깎은 정다면체

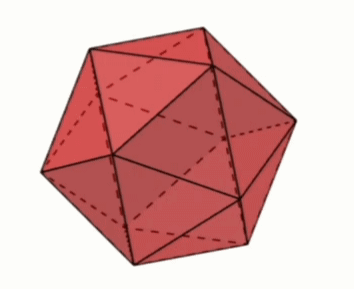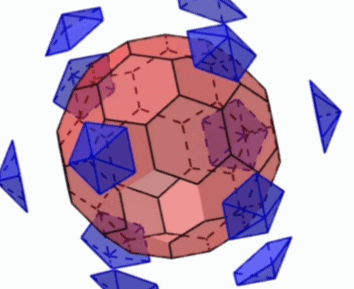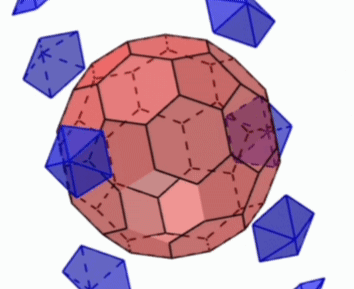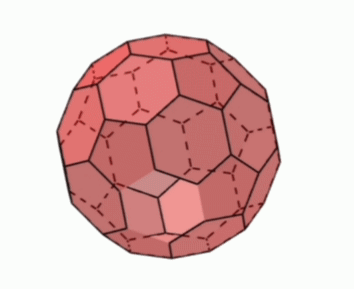
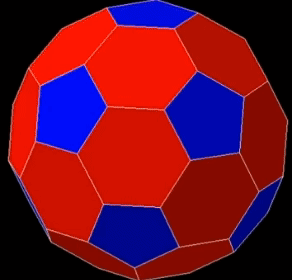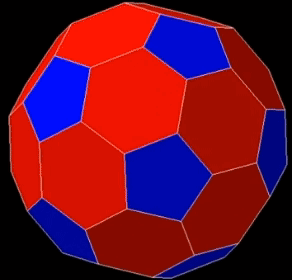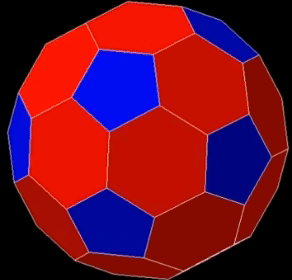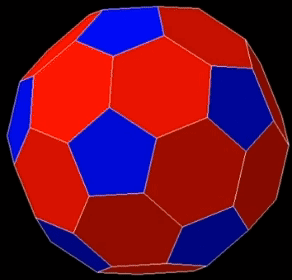
[문제] 정이십면체의 꼭짓점에서 모서리의 ${\displaystyle \frac{1}{3}}$만큼 잘라내서 만든 축구공모양의 입체도형(깎은이십면체)에 대하여 다음에 답하여라.

1. 면의 종류와 개수
2. 꼭짓점 개수
3. 모서리 개수

[풀이]

1. 면의 종류 : 정육각형, 정오각형
   이십면체의 면 $\to$ 정육각형 20개
   꼭짓점이 잘린 곳 $\to$ 정오각형 12개
2. 꼭짓점 개수
   육각형 20개 오각형 12개 이므로 중복을 허용하여 개수를 세고 중복 횟수 만큼 나누어 계산.
   $6\times 20+5\times 12=180$$\underset{\text{중복:3}}{\overset{÷3}{\to }}{\displaystyle \frac{180}{3}}=60$개
3. 모서리 개수
   육각형 20개 오각형 12개 이므로 중복을 허용하여 개수를 세고 중복 횟수 만큼 나누어 계산.
   $6\times 20+5\times 12=180$$\underset{\text{중복:2}}{\overset{÷2}{\to }}{\displaystyle \frac{180}{2}}=90$개

전개도 활용 문제

전개도와 위치관계

[문제] 주어진 전개도를 이용해 만든 정팔면체의 변 $\overline{AD}$와 꼬인위치에 있는 선분을 구하여라.

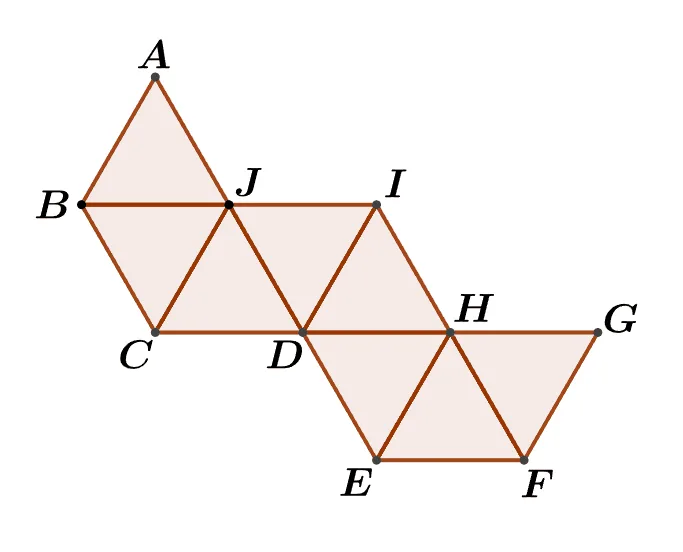
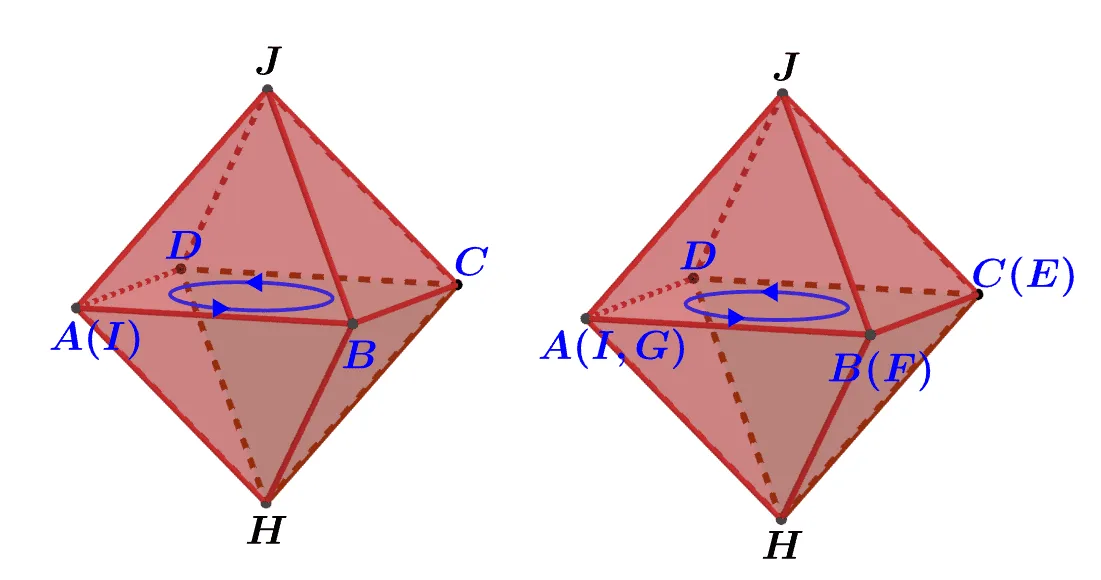
[풀이]

전개도를 이용해 입체도형의 꼭짓점의 기호를 붙일 때는 방향성을 가지고 순서대로 기호를 붙이면 된다. (반시계 방향)

• $A\to B\to C\to D\to I(=A)$
• $I\to D\to E\to F\to G(=A)$

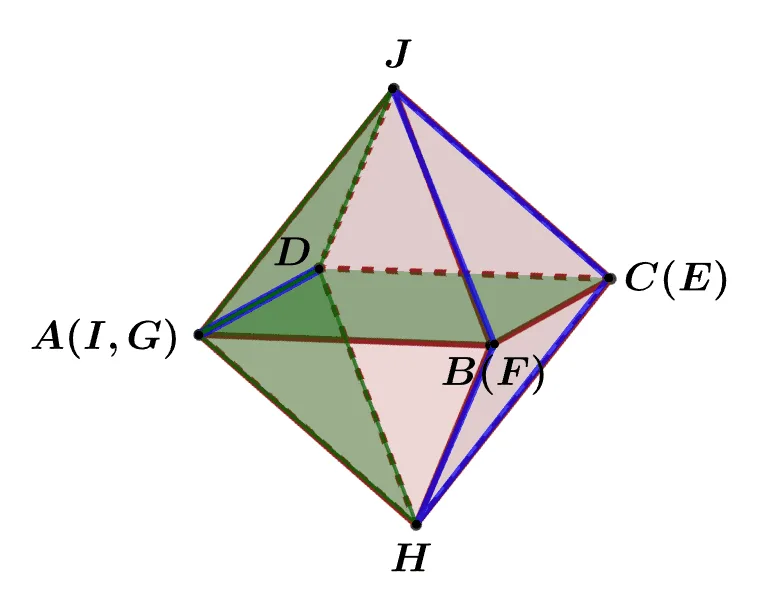
$\overline{AD}$와 꼬인위치를 찾는 방법은 다음과 같다.

꼬인위치는 평면상의 위치관계가 아니므로 $\overline{AD}$와 한 평면에 있을 수 있는 선분을 제외 한다.

• $\mathrm{△}JAD,\mathrm{△}HAD,\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}ABCD$위의 선분 제외

나머지 선분은 $\overline{AD}$와 만나지도 평행하지도 않고 따라서 꼬인위치라고 할 수 있다.

$\overline{JB},\overline{JC},\overline{HB},\overline{HC}$

전개도에서 만나는 점 찾기

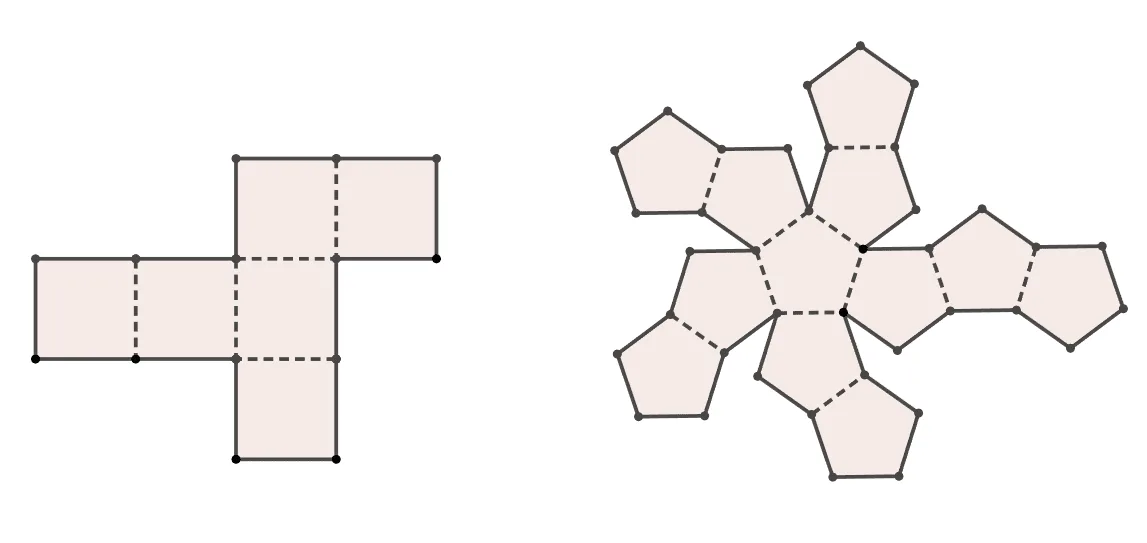
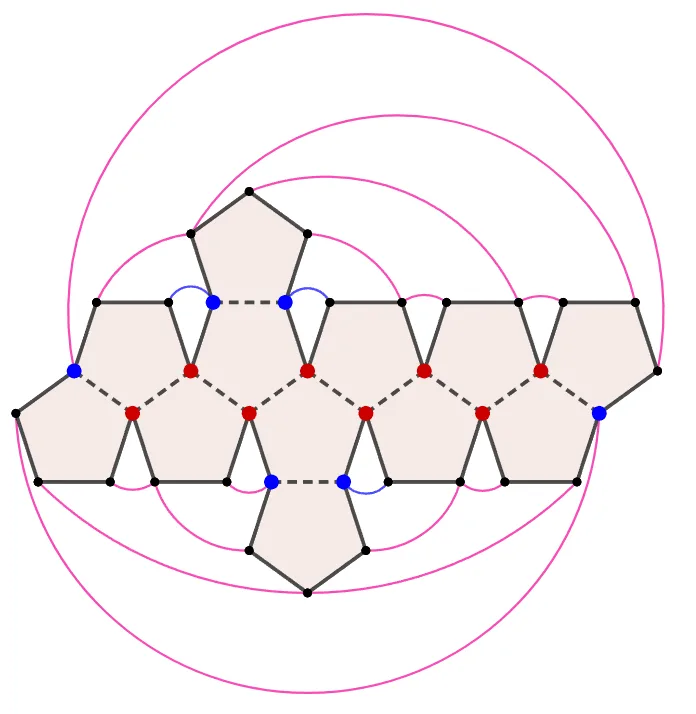
[문제] 전개도에서 만나는 점을 선으로 연결하여라.

[풀이]

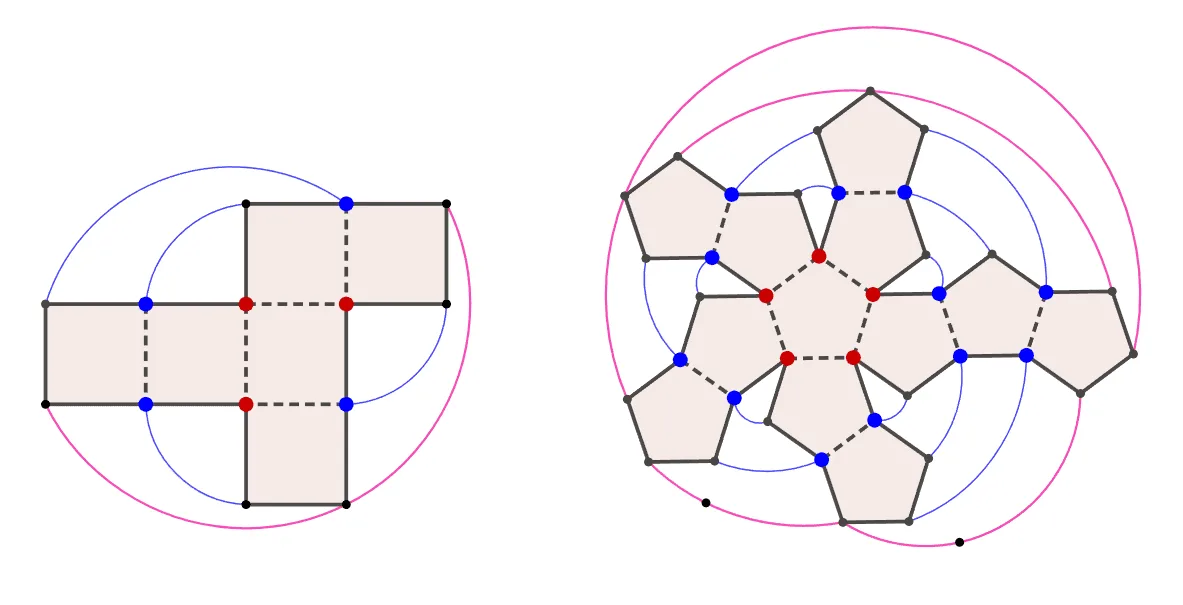
정육면체와 정십이면체는 한 꼭짓점에서 만나는 면의 개수가 3개이다.

• $\bullet$: 연결 안함 (3개 만남)
• $\bullet$: 면 하나와 연결
• $\bullet$: 면 두개와 연결

다음 문제에 다시 한번 적용해 보세요.

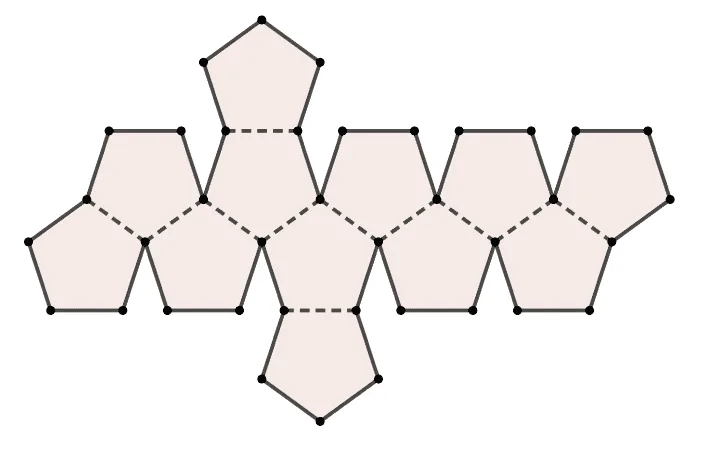
전개도와 최단거리

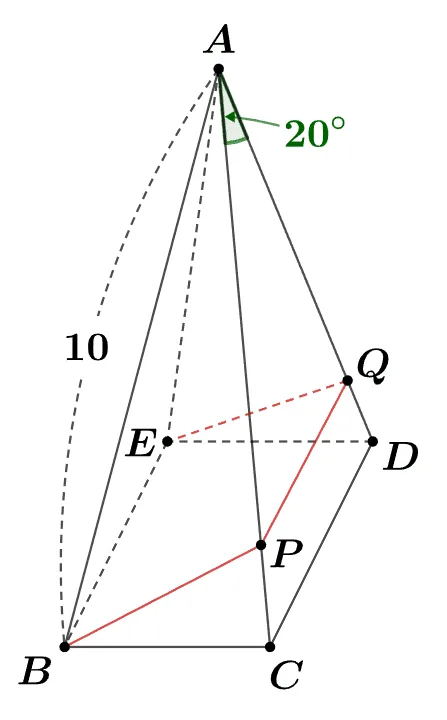
[문제] 밑면 $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/15.1.0/svg/25fb.svg">}BCDE$가 정사각형이고 $\mathrm{\angle }ACD={20}^{\circ }$인 사각뿔 A-BCDE에 대하여 꼭짓점 $B$에서 $\overline{AC},\overline{AD}$위의 점 $P,Q$를 지나 꼭짓점 E까지 이르는 최단거리를 구하여라.

[풀이]

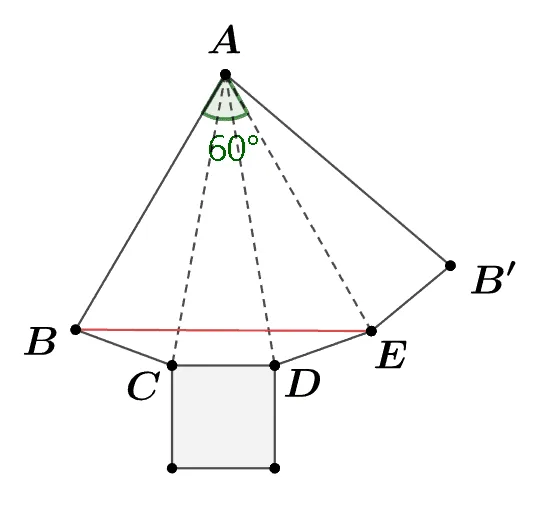
사각뿔의 전개도에서 직선 거리 $\overline{BE}$가 최단거리이다.

• $\mathrm{\angle }BAE={60}^{\circ }$이고 $\overline{AB}=\overline{AE}$이므로 $\mathrm{△}ABE$는 정삼각형이다.

따라서 $\overline{BE}=10$이다.

이상으로 다면체에 관련된 문제풀이를 마무리 하도록 하겠습니다.