삼각형의 내심은 세 내각의 이등분선이 만나는 점으로, 내접원의 중심이라는 사실은 널리 알려져 있습니다. 하지만 단순한 정의를 넘어서, 내심의 응용은 삼각형의 넓이, 접선의 길이, 각의 크기 계산 등 다양한 문제에 등장합니다.
이 글에서는 내심의 개념을 실제 문제에 어떻게 적용할 수 있는지를 세 가지 대표 응용을 통해 구체적으로 살펴봅니다. 단순한 이론 암기를 넘어, 내심을 도구로 활용하는 사고 과정까지 함께 익히고자 한다면, 끝까지 읽어보시길 권합니다.
목차
내심과 삼각형의 넓이
삼각형의 세 변의 길이가 주어질 때 함께 삼각형의 넓이를 내접원의 반지름을 이용해 간단한 공식으로 계산할 수 있습니다.
내접원의 반지름과 삼각형의 넓이
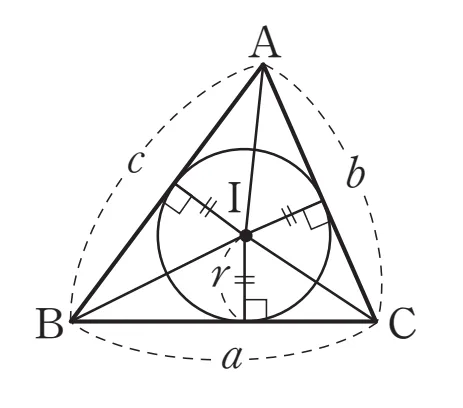
내접원의 반지름을 $r$이고, 세 변의 길이를 각각 $a,\;b,\;c$인 $\triangle{ABC}$의 넓이는 다음과 같이 표현할 수 있습니다.
$\triangle{ABC} = \dfrac{1}{2} \times (a + b + c) \times r $
[증명]
삼각형 $\triangle{ABC}$에 내접하는 원의 중심을 $I$, 내접원의 반지름을 $r$에 대하여 $\triangle{ABC}$의 넓이는 다음과 같습니다.
- $\triangle{ABC}=\triangle {ABI} + \triangle {BCI} + \triangle {CAI}$
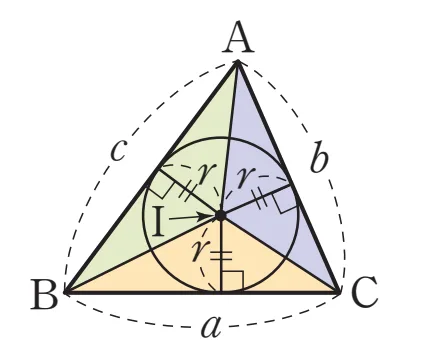
각 부분 삼각형의 넓이는 밑변과 높이를 이용하여 다음과 같이 나타낼 수 있습니다.
- $\triangle{ABI} = \dfrac{1}{2} \times c \times r$
- $\triangle{BCI} = \dfrac{1}{2} \times a \times r$
- $\triangle{CAI} = \dfrac{1}{2} \times b \times r$
변변 더하면 $\triangle{ABC}$의 넓이는 다음과 같습니다.
- $\triangle{ABC} = \dfrac{1}{2} \times (a + b + c) \times r $
예제
세 변의 길이가 각각 $6cm,\ 8cm,\ 10cm$ 이고, 넓이가 $24cm^2$인 $\triangle{ABC}$의 내접원의 반지름 $r$을 구하시오.
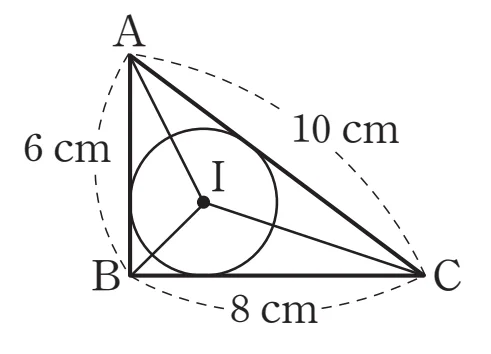
- $\triangle{ABC}=\dfrac{1}{2} \times (6+8+10) \times r = 24$
위의 방정식을 풀면 내접원의 반지름을 구하면 다음과 같습니다.
\begin{flalign} \dfrac{1}{2} \times (24) \times r &= 24\\
r&=2&& \end{flalign}
내심과 접선의 길이
교육과정에서 접선의 길이는 중학교 2학년에서는 내심과 관하여 정리하고, 중학교 3학년에서는 원 밖의 한 점에서 그은 두 접선의 길이로 정리합니다. 이 두가지 내용은 정확히 같은 의미를 가지고 있습니다.
중학교 3학년에서는 접선의 성질을 삼각형에서 사각형으로 확장하여 다루고 사각형의 내심이 존재할 조건에 대해서도 다루게 됩니다. (중학교 3학년 듀란드 정리)
- 사각형이 원에 외접하면 마주보는 변의 길이 합이 같다.
- 마주보는 변의 길이 합이 같은 사각형은 원에 외접한다. (사각형의 내심이 존재할 조건)
내접원과 접선의 길이
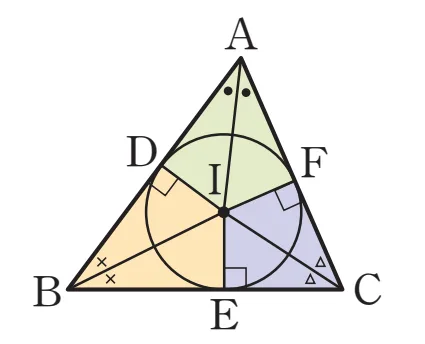
삼각형 $\triangle ABC$에 내접하는 원이 세 변 $\overline{AB}$, $\overline{BC}$, $\overline{CA}$에 접하는 점을 각각 $D$, $E$, $F$라 하면 다음이 성립합니다.
- $\overline{AD} = \overline{AF}$
- $\overline{BE} = \overline{BD}$
- $\overline{CE} = \overline{CF}$
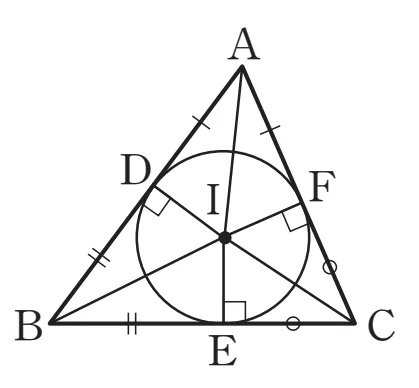
[증명]
$I$가 내심이므로 $\overline{DI}=\overline{EI}=\overline{FI}$이고 따라서 다음이 성립합니다. (RHS 합동)
- $\triangle{ADI} \equiv \triangle{AFI}$, $\Rightarrow \overline{AD} = \overline{AF}$
- $\triangle{BDI} \equiv \triangle{BEI}$, $\Rightarrow \overline{BE} = \overline{BD}$
- $\triangle{CEI} \equiv \triangle{CFI}$, $\Rightarrow \overline{CE} = \overline{CF}$
따라서 $\overline{BE}$의 길이는 다음을 이용하여 구할 수 있습니다.
- $\overline{AB}+\overline{BC}-\overline{CA}=2\times\overline{BE}$
직각삼각형에서 내접원의 반지름
아래의 직각삼각형 $\triangle{ABC}$의 내심$I$에 대하여, 접점을 지나는 내접원의 반지름을 연결할 때 생기는 $\square{IDCE}$는 다음과 같은 이유로 정사각형이 됩니다.
- 네 각의 크기가 직각(직사각형), 이웃하는 변의 길이가 같다.
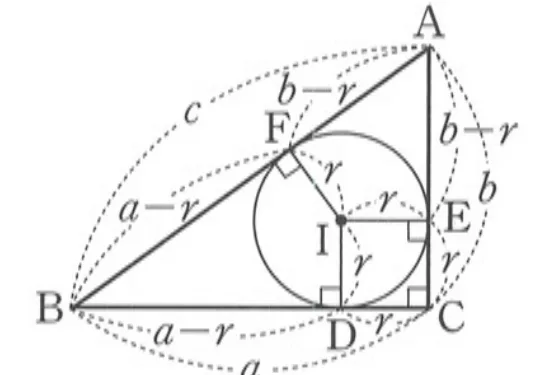
따라서 빗변의 길이가 $c$이고, 빗변이 아닌 두 변의 길이가 $a,\ b$일 때 내접원의 반지름 $r$은 다음을 만족합니다.
- $a+b-c=2r$
예제
삼각형 $\triangle ABC$의 세 변의 길이가 각각 $\overline{AB} = 15$, $\overline{BC} = 13$, $\overline{CA} = 12$일 때, $\overline{BD}$의 길이를 구하여라.
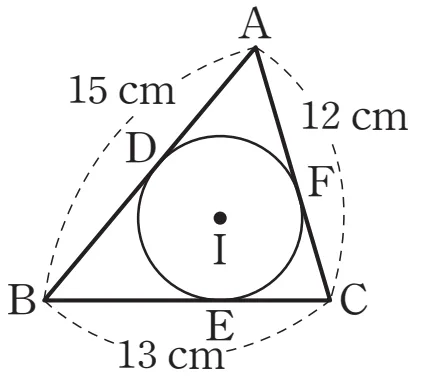
$\overline{BD} = \overline{BE} = x$로 두면, 다음이 성립합니다.
- $\overline{CE} = \overline{CF} = 13-x$
- $\overline{AD} = \overline{AF} = 15-x$
\begin{flalign}\overline{CA}&=\overline{AF}+\overline{CF}\\
&=(13-x)+(15-x)=12&&\end{flalign}
위의 식을 풀면 $\overline{BD}=8$임을 알 수 있습니다.
내심과 각의 크기
내심은 세 각의 이등분선이 만나는 점으로, 이를 기준으로 나누어진 각의 관계를 이용하면 여러 각의 크기를 효율적으로 구할 수 있습니다.
내심과 삼각형의 각의 크기1
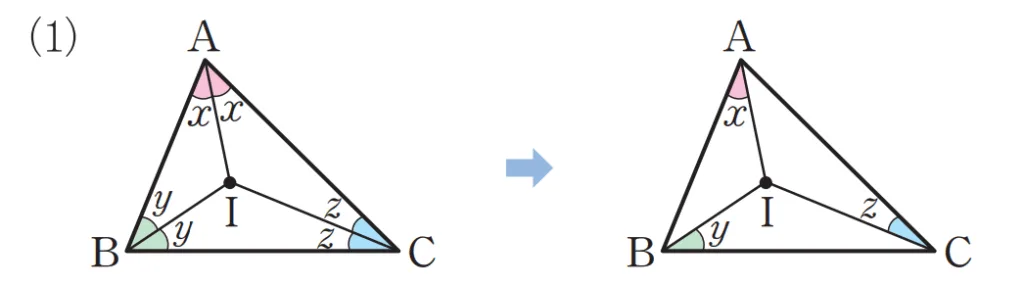
$\triangle{ABC}$의 내심$I$에 대하여 다음이 성립합니다.
- $\angle{x} + \angle{y} + \angle{z} = 90^\circ$
[증명]
$I$가 내심이므로 $\overline{AI},\;\overline{BI},\;\overline{CI}$는 각의 이등분선이고 $\angle{A},\;\angle{B},\;\angle{C}$의 이등분된 각을 각각 $x,\; y,\;z$라고 할 때, 다음을 만족합니다.
- $\angle{A}=2x$, $\angle{B}=2y$, $\angle{C}=2z$
삼각형의 세 내각의 크기의 합은 항상 $180^\circ$이므로, $\angle{A} + \angle {B} + \angle {C} = 180^\circ$ 이고 따라서 다음이 성립합니다.
- $2x+2y+2z=180^\circ$ $\Rightarrow\; x+y+z=90^\circ$
예제
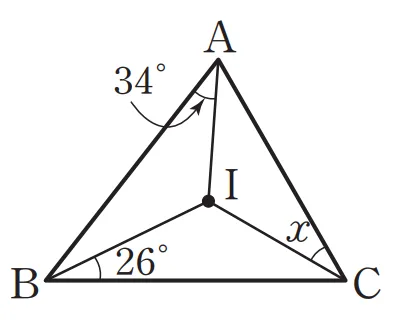
$\triangle{ABC}$의 내심 $I$에 대하여 각 $x$의 크기를 구하여라.
$34^\circ+26^\circ+\angle{x}=90^\circ$이고 따라서
$x=30^\circ$ 입니다.
내심과 삼각형의 각의 크기2
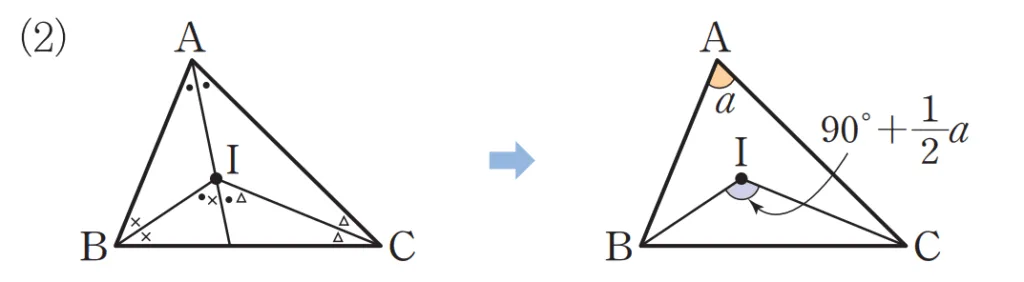
$\triangle{ABC}$의 내심$I$에 대하여 다음이 성립합니다.
- $\angle{BIC} = 90^\circ + \dfrac{1}{2} \angle{a}$
[증명]
$I$가 내심이므로 $\overline{AI},\;\overline{BI},\;\overline{CI}$는 각의 이등분선이고 $\angle{A},\;\angle{B},\;\angle{C}$의 이등분된 각을 각각 $x,\; y,\;z$라고 할 때, 다음을 만족합니다.
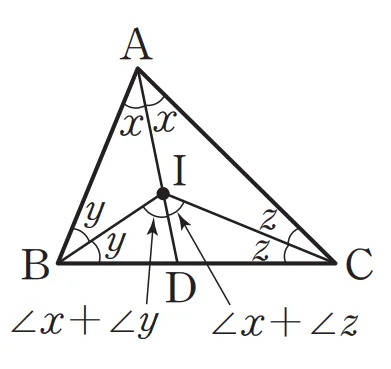
선분 $\overline{BC}$의 연장선과 $\overline{BC}$가 만나는 점을 $D$로 두고, $\angle{BIC}$를 삼각형 $\triangle ABI$와 $\triangle ACI$의 외각의 합으로 생각하면 다음과 같습니다.
- $\angle{BID}=x+y$
- $\angle{CID}=x+z$
변변 더하여 정리하면 다음과 같습니다.
\begin{flalign} \angle{BIC} &= \angle{BID}+\angle{CID}\\
&=x+\bbox[#ffff00]{x+y+z}\\
&=\bbox[#ffff00]{90^\circ} + \bbox[#dcff8d]{x} &&\end{flalign}
따라서 다음과 같은 결과를 얻을 수 있습니다.
- $\angle{BIC} =\bbox[#ffff00]{90^\circ} + \bbox[#dcff8d]{\dfrac{1}{2}\angle{a}}$
예제
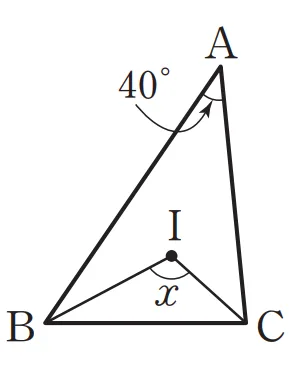
$\triangle{ABC}$의 내심 $I$에 대하여 각 $x$의 크기를 구하여라.
$\angle{x}=90^\circ+\dfrac{1}{2}\times 40^\circ$이고 $\angle{x}=110^\circ$입니다.
.
