도수분포표로 정리된 수많은 데이터를 어떻게 시각화하면 좋을까요?
바로 히스토그램과 도수분포다각형이 그 역할을 해줍니다.
이번 수업에서는 도수분포표를 히스토그램으로, 그리고 다시 도수분포다각형으로 변환하는 과정을 따라가며 각 그래프가 보여주는 통계적 의미와 한계에 대해 알아보았습니다. 히스토그램은 도수의 절대적인 분포를 보여주는 데에 강점을 가지지만, 두 집단을 비교하기에는 한계가 있습니다. 반면 도수분포다각형은 두 집단의 흐름이나 경향성을 직관적으로 파악하기에 더 유리한 도구입니다.
단순히 그래프를 그리는 기술을 넘어, 어떤 그래프가 어떤 상황에 적절한지를 판단하는 통계적 사고력을 키울 수 있는 시간이 될 것 입니다.
목차
히스토그램
히스토그램 : 도수분포표를 그래프로 나타낸 것
히스토그램을 그리는 과정
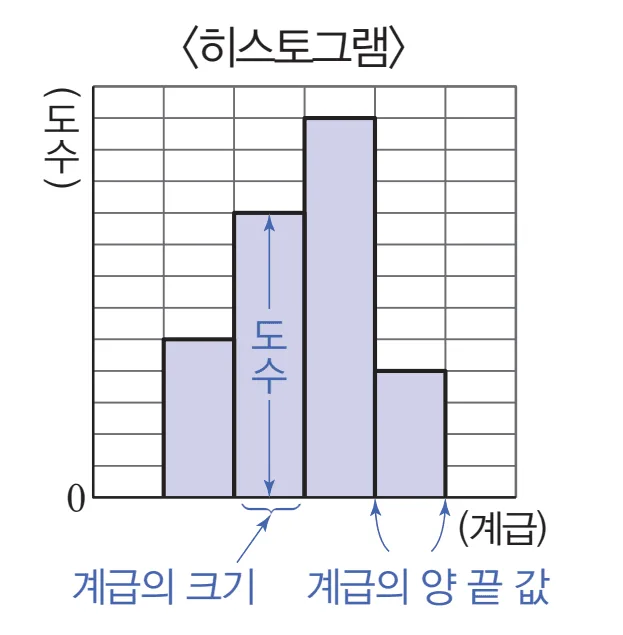
- 가로축 : 계급의 양 끝값
- 세로축 : 도수
- 직사각형을 그린다.
- 가로 길이: 계급의 크기
- 세로 길이 : 도수
- 직사각형 개수 : 계급의 개수
히스토그램 그리기
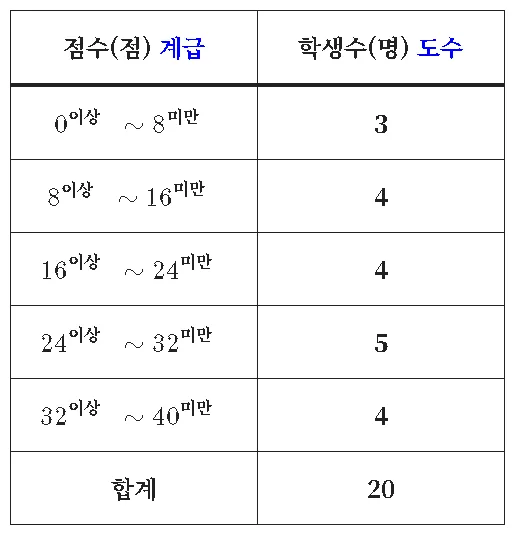
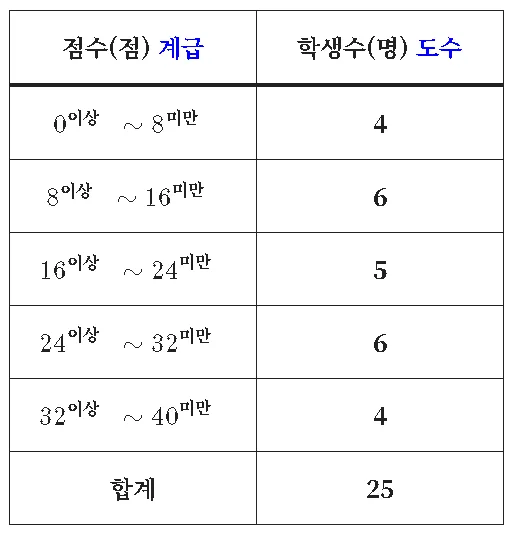
두 학급 $A,\;B$ 의 수학 단원평가 점수를 도수분포표로 나타낸 자료를 히스토그램으로 표현해 보자.
도수분포표
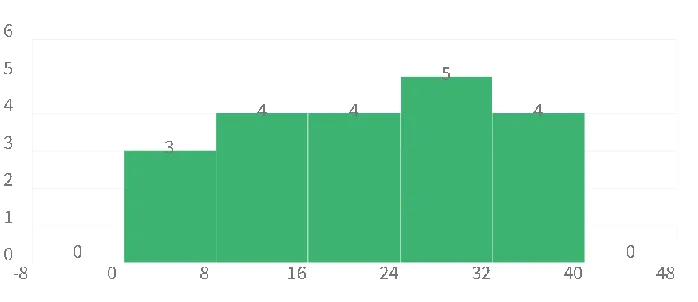
히스토그램
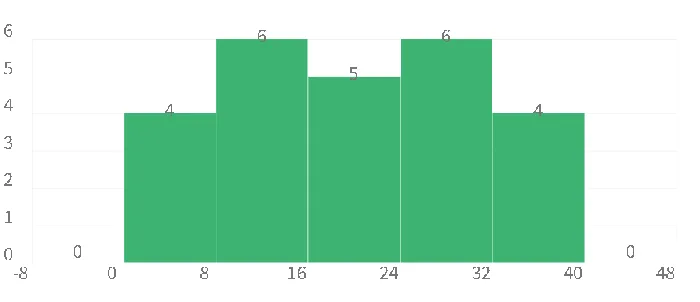
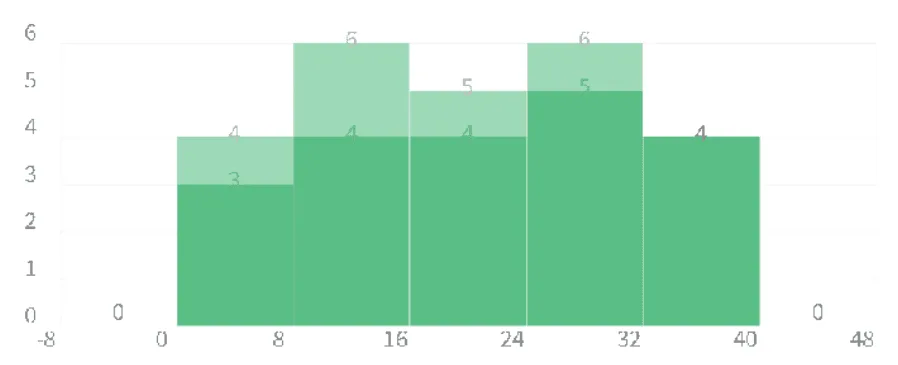
두 집단의 비교
다음과 같은 이유로 두 집단을 히스토그램을 이용해 비교하는 것은 효과 적이지 않다.
- 색이 겹쳐 두 집단을 비교하는데 사용하기 어려움.
히스토그램의 특징 제한점
특징
- 자료의 전체적 분포를 시각적으로 보여줌
- 직사각형 넓이 도수에 비례
- 직사각형 넓이 총합 : (계급의 크기)$\times$ (도수 총합)
제한점
- 두 집단을 비교하는데 적절하지 않음.
- 원자료 손실
- 계급의 크기, 개수에 따른 왜곡 편차
도수분포다각형
히스토그램의 양끝에 도수가 0일 계급을 추가하고 각 직사각형 윗변의 중점을 선분으로 연결한 것을 도수분포 다각형이라고 한다.
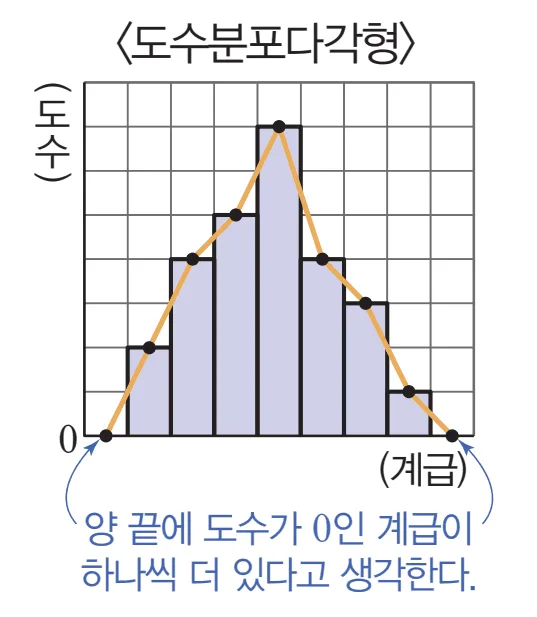
도수분포다각형 그리는 과정
- 도수분포표 $\rightarrow$ 히스토그램
- 각 직사각형 윗변의 중점을 선분으로 연결
- 양 끝에 도수가 0인 계급을 하나씩 추가, 중점을 선분으로 연결
도수분포 다각형 그리기
$A,\;B$ 두 반의 단원평가 점수에 대한 히스토그램을 이용해 도수 분포 다각형을 그리면 다음과 같다.
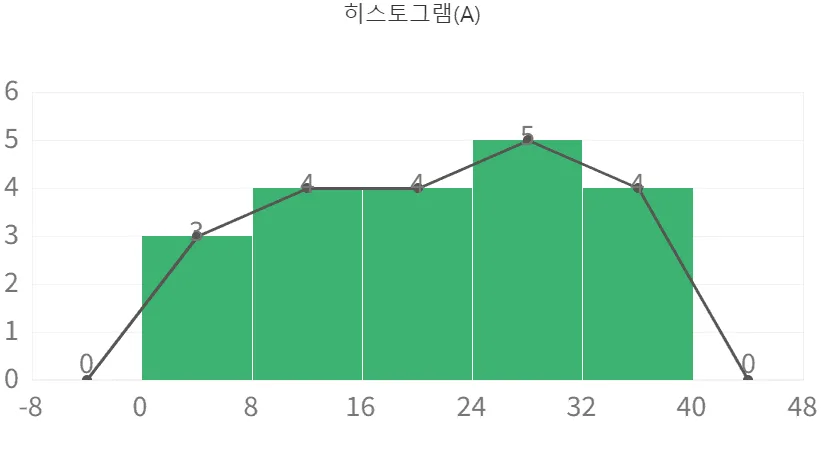
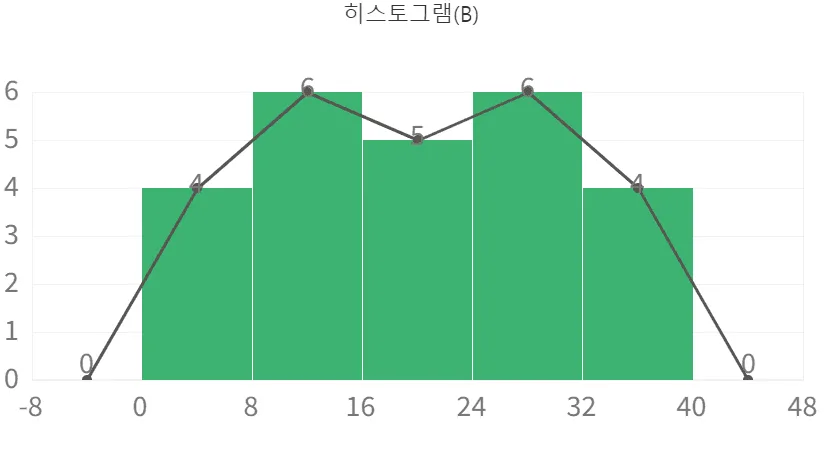
위의 과정에서 알 수 있듯이 히스토그램을 이용하지 않고 도수분포다각형을 그리는 방법을 정리하면 다음과 같다.
- (계급값, 도수) $\rightarrow$ 좌표 $\rightarrow$ 선분연결
도수분포다각형의 넓이
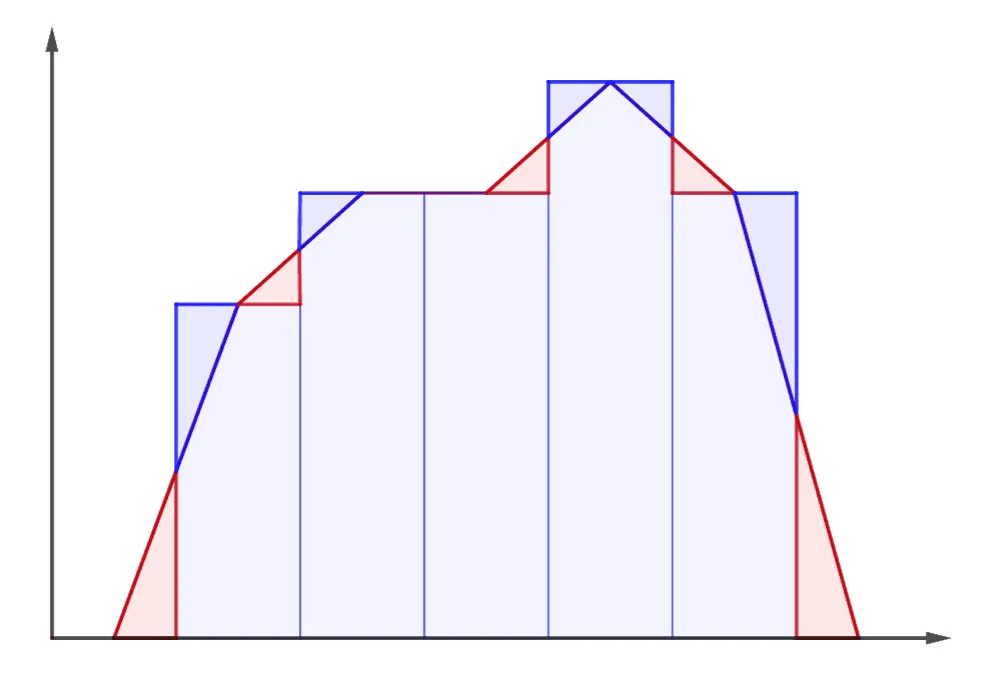
도수분포 다각형의 넓이와 히스토그램의 넓이를 비교하면 다음과 같다.
- (도수분포 다각형과 $x$축 사이의 넓이)
$=$ (히스토그램 직사각형 넓이 합)
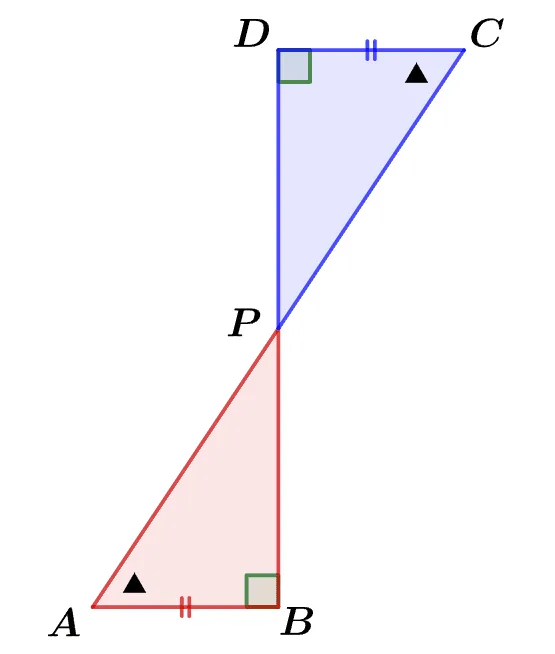
\begin{flalign}
\triangle{PAB}&\equiv \triangle{PCD}\\[1em]
&\overline{AB}=\overline{CD}\\[1em]
&\angle{PAB}=\angle{PCD}\\[1em]
&\angle{ABP}=\angle{CDP}\\[1em]
\triangle{PAB}&=\triangle{PCD}
&&\end{flalign}
따라서 도수분포다각형과 $x$축으로 둘러싸인 면적은 히스토그램의 사각형 면적과 동일하다.
\begin{flalign}
\therefore\; &\text{도수분포다각형면적}\\[1em]
&=(\text{계급의 크기}) \times (\text{도수 총합})
&&\end{flalign}
두집단 비교
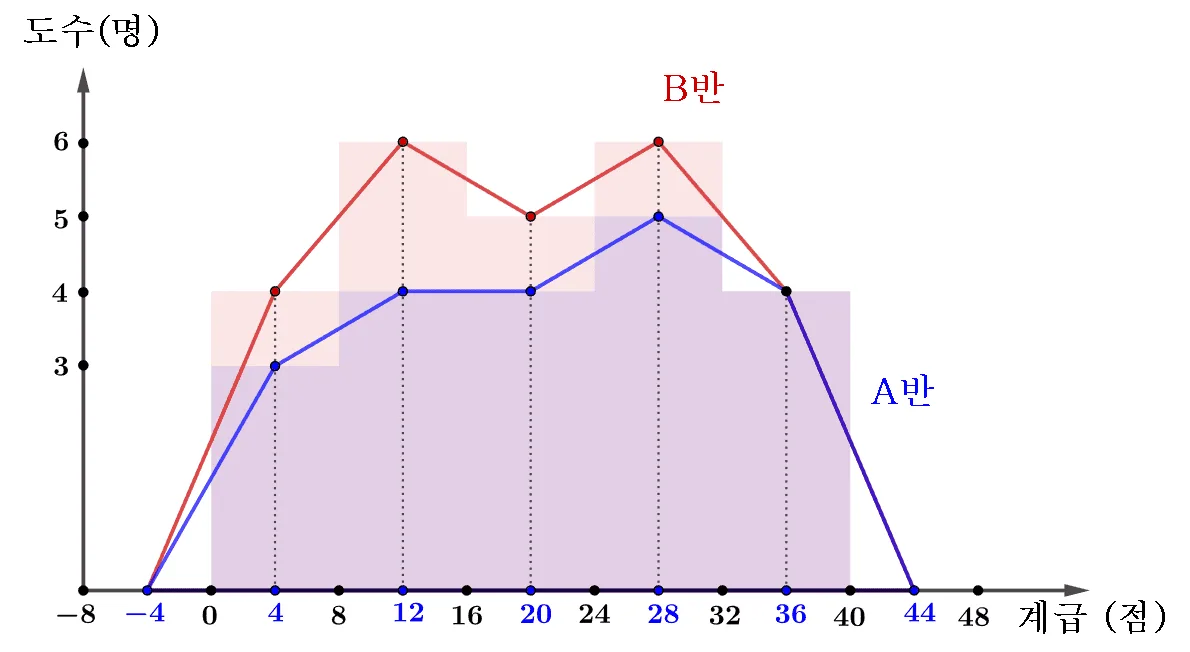
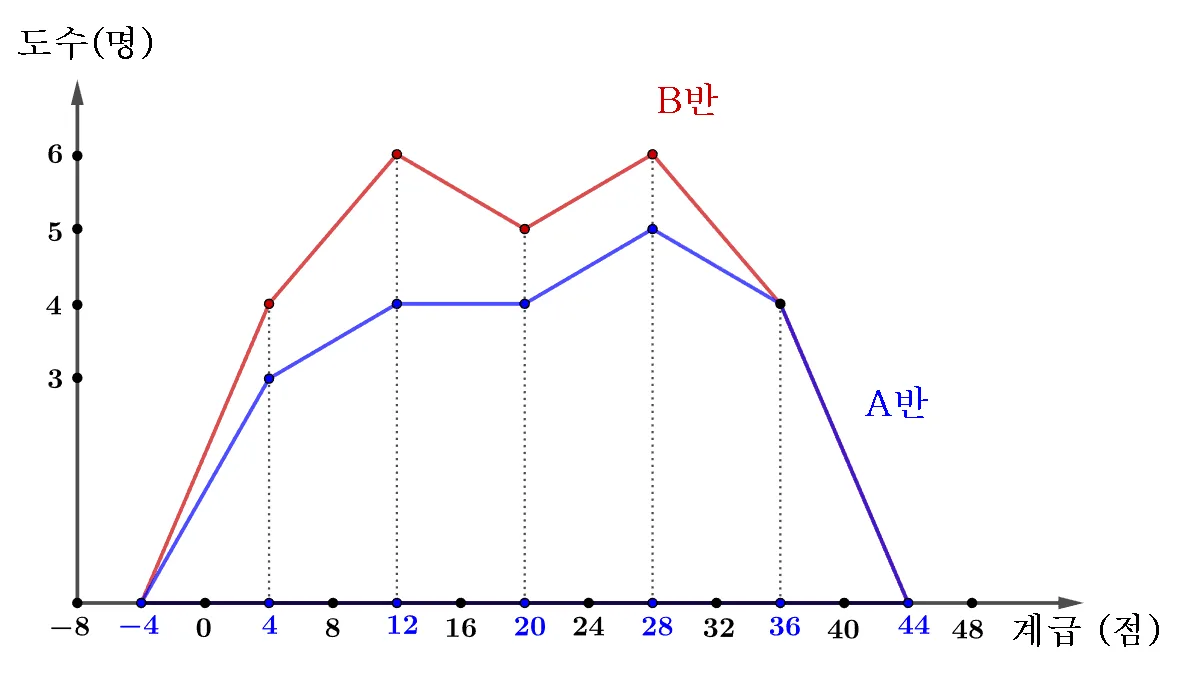
두 집단을 비교할 때 히스토그램보다 도수분포 다각형이 유리하다.
주의사항
위의 결과를 통해 $B$반의 성적이 더 좋다고 할 수 있을까?
- A반과 B반의 전체 학생수(도수의 총합)가 다르기 때문에 이렇게 단정 지을 수 없다.
이러한 경우에는 각 계급의 도수를 전체 학생수에 대한 비율로 바꾸어 생각할 필요가 있다.
도수분포다각형의 특징, 제한점
특징
- 데이터의 연속적인 변화를 시각적으로 표현
- 중심 경향, 대칭성을 직관적으로 파악
- 두 집단을 겹쳐서 비교
제한점
- 도수의 총합이 다른 두 집단을 비교할 때 주의
- 원자료의 손실
- 계급설정에 따른 왜곡, 편차
다음 수업에서는 도수의 총합이 다른 집단을 비교하는 방법에 대해 살펴보도록 하겠습니다.
중고등학교 통계 프로그램 사이트
중고등학교 통계수업에 활용할 수 있는 프로그램을 제공하는 사이트 입니다.
