이번 시간에는 고등학교 수학을 준비하는 학생을 위해 2023년 3월 고1 모의고사 수학 객관식 문제 19, 20, 21에 대한 풀이를 살펴보려고 합니다. 19, 20, 21 번을 제외한 나머지 문제는 학생들이 직접 해결해 보길 바란다.
다운로드
목차
2023년 3월 고1 모의고사 19

풀이
1단계 (거꾸로 풀기)
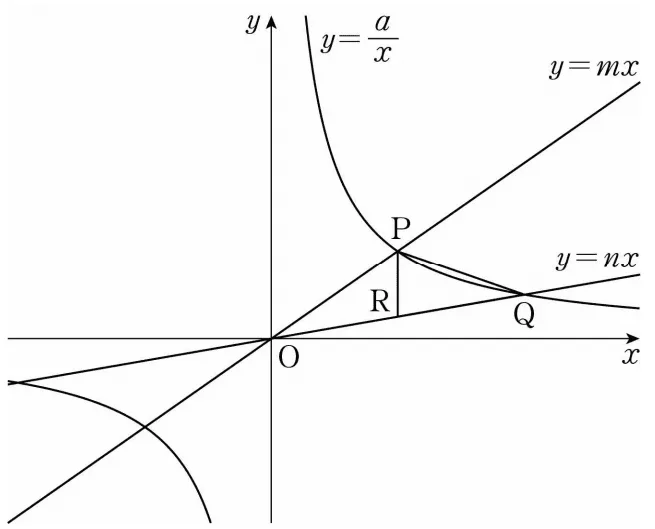
문제에서 삼각형의 넓이에 대한 값이 주어졌다. 따라서 정해진 값을 식으로 표현하면 문자들 사이의 관계를 알 수 있음을 빠르게 파악하는 것이 문제를 해결하는 첫 걸음이다. 삼각형의 넓이를 표현하는 과정은 아래와 같다.
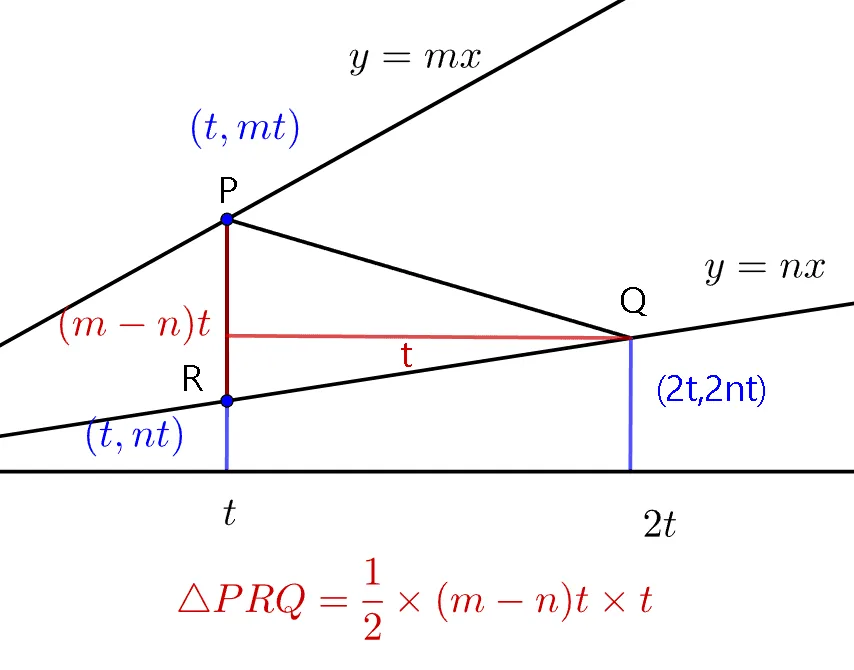
$P$의 $x$ 좌표를 $t$ 라고 두면 $\triangle{PQR}=\dfrac{1}{2}\times(m-n)t\times t=\dfrac{3}{2}$ 임을 알 수 있다. 이를 정리하면 다음과 같은 식을 얻을 수 있다.
- $(m-n)t^2=3$
2단계 풀이
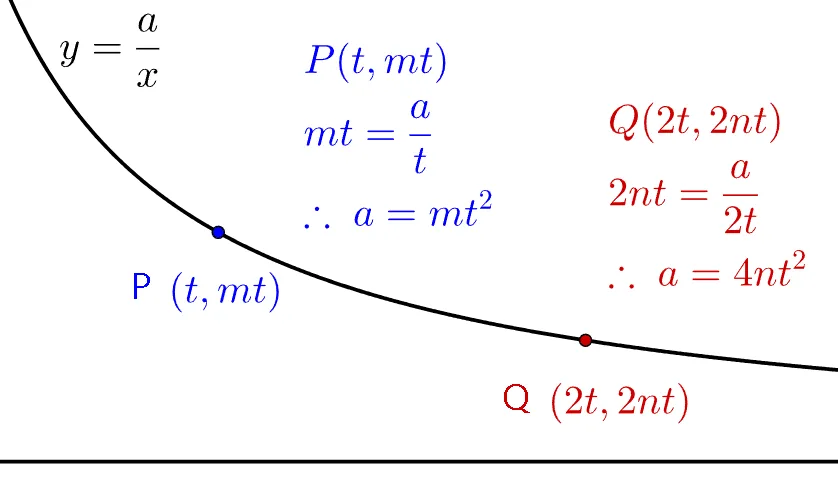
아직 사용하지 않은 조건을 이용하여 식을 더 만들면 문제를 해결할 수 있다. $P$, $Q$는 $y=\dfrac{a}{x}$위의 점이란 사실을 아직 이용하지 않았으므로 이를 이용해 식을 정리하면 다음과 같은 식을 얻을 수 있다.
3단계 식 정리
1,2단계에서 얻은 아래의 식을 연립하여 $a$ 값을 구하면 문제를 해결 할 수 있다.
$$\begin{align} &(m-n)t^2=3 \tag{1}
\\& a=mt^2 \tag{2}
\\& a=4nt^2 \tag{3}&&
\\& \end{align}$$
(2)와 (3)식을 연립 하면 $mt^2=4nt^2$이고, $t\neq0$ 일 때 다음이 성립한다.
$m=4n\tag{4}$
(1), (4)식을 연립 하면
$(m-n)t^2=3\;\rightarrow\;(4n-n)t^2=3\;\rightarrow\;nt^2=1$
이 결과를 (3)식에 대입하면 $\therefore\;a=4nt^2=4$
2023년 3월 모의고사 20

풀이
1단계(거꾸로 풀기)
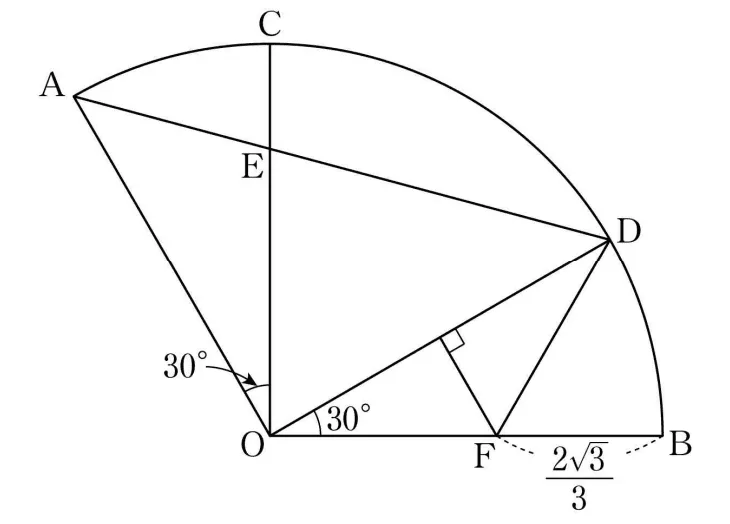
$\triangle{ODE}$의 넓이를 구할 수 있는 방법을 먼저 생각해 보자.
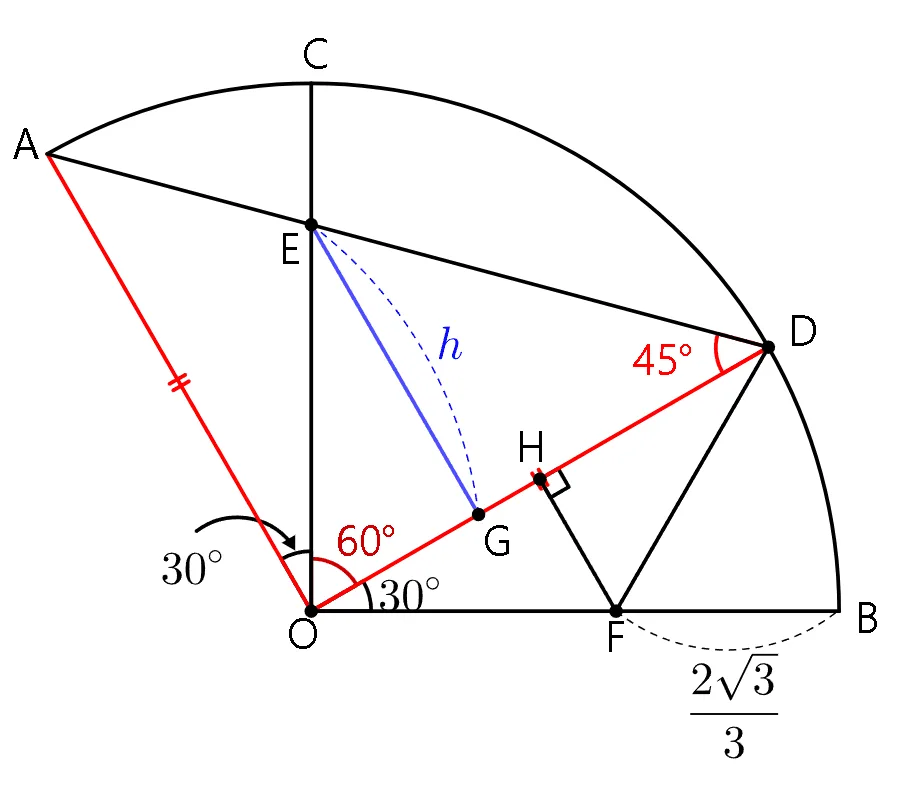
$\angle{EOD}=60^{\circ},\; \angle{AOD}=90^{\circ}$
$\overline{OA}=\overline{OD}\;\rightarrow\;\angle{ADO}=45^{\circ}$
따라서 $\overline{OD}$의 길이를 구하면 양 끝각이 특수각 이므로 $\triangle{ODE}$의 넓이를 삼각비를 이용해 구할 수 있다.
2단계 $\overline{OD}$ 구하기
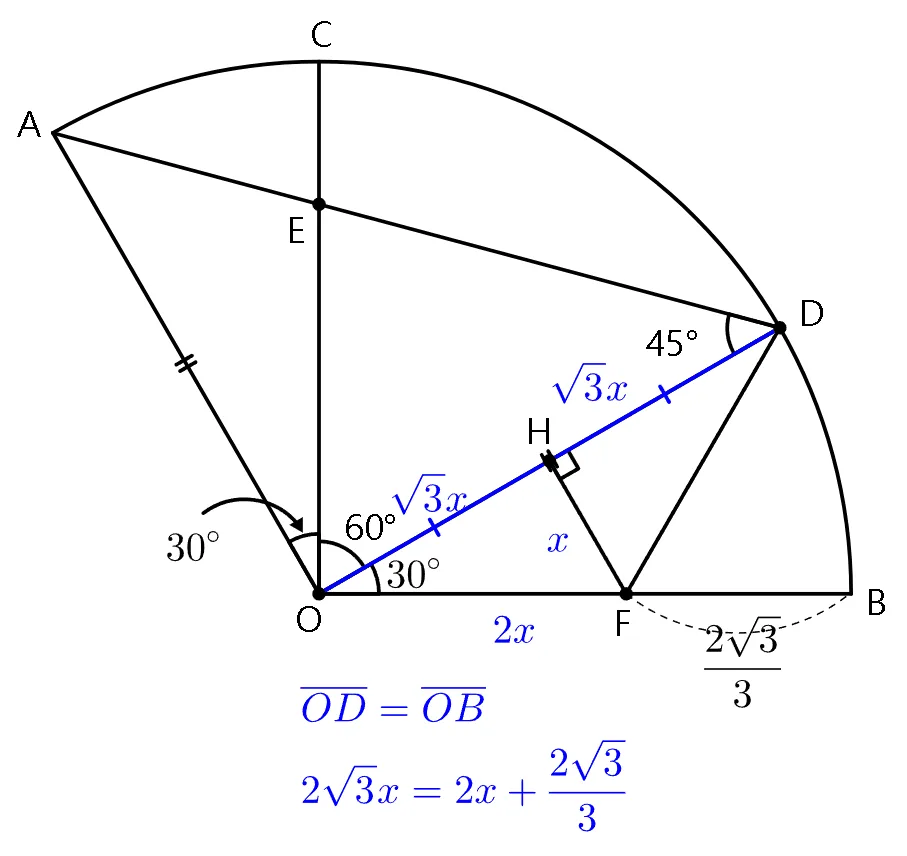
$\overline{HF}$는 $\overline{OD}$의 수직 이등분선
$\triangle{OHF}\equiv\triangle{DHF}(SAS)$
$\overline{HF}=x$라고 할 때
$\overline{OH}=\overline{HD}=\sqrt3x$이고
$\overline{OF}=2x$이다.
$\overline{OD}=\overline{OB}$임을 이용하면
$2\sqrt3x=2x+\dfrac{2\sqrt3}{3}$
$\therefore\;x=\dfrac{3+\sqrt3}{6}$
$\overline{OD}=2\sqrt3 \times x=\sqrt3+1$
3단계 $\triangle{ODE}$ 넓이 구하기
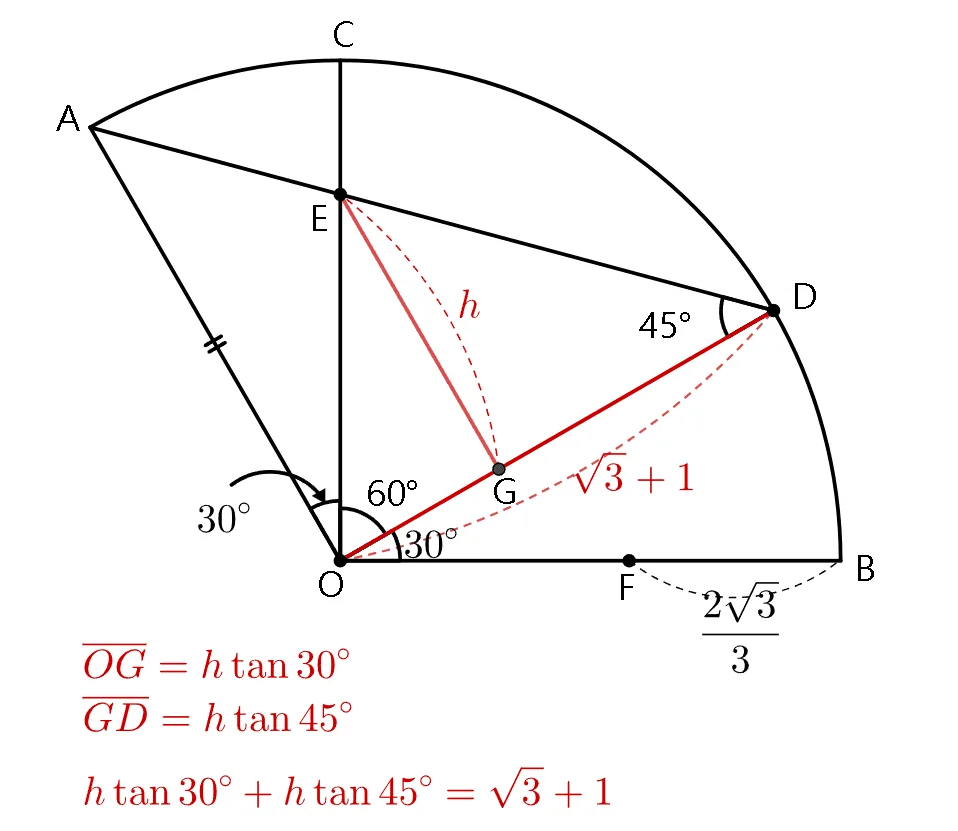
$\triangle{ODE}$ 높이는 삼각비를 이용해 구할 수 있다.
$\angle{OEG}=30^{\circ},\;\angle{DEG}=45^{\circ}$
$\overline{OG}=h\tan30^{\circ},\;\overline{DG}=h\tan 45^{\circ}$
$h\tan30^{\circ}+h\tan 45^{\circ}=\sqrt3+1$
$h=\dfrac{\sqrt3+1}{\tan30^{\circ}+\tan45^{\circ}}$
$h=\sqrt3$
$\triangle{ODE}=\dfrac{1}{2}\times\overline{OD}\times h$
$\therefore\; \triangle{ODE}=\dfrac{3+\sqrt3}{2}$
2023년 3월 모의고사 21

풀이
ㄱ. $\angle{BID}=\angle{IBD}$ (참)
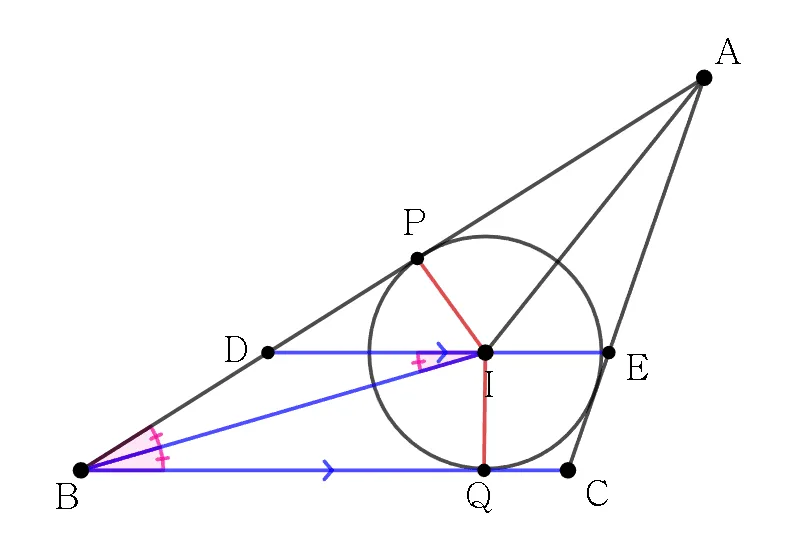
내심 $I$를 지나는 평행선 $\overline{DE}$에 대해
$\triangle{BIP} \equiv \triangle{BIQ}\;(\because RHS)$
$\therefore\; \angle{IBP}=\angle{IBQ}$이고
$\overline{DE}//\overline{BC})$이므로
$\angle{IBQ}=\angle{BID}$이다.
내심 $I$를 지나는 평행선 $\overline{DE}$에 대해 다음이 성립함을 알아두자.
- $\triangle{DIB}$ : 이등변 삼각형
ㄴ. [ $\triangle{ADE} 둘레 ] = 7\sqrt{2}$ (참)
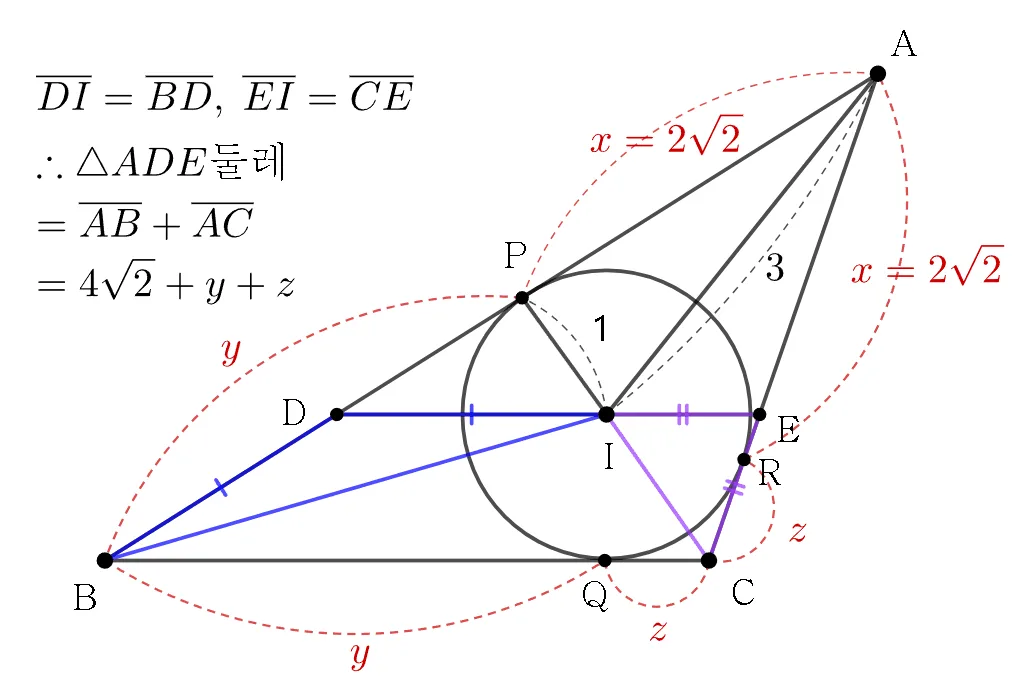
- ㄱ 의 결과를 정리하면 $\overline{DI}=\overline{BD},\;\overline{EI}=\overline{CE}$이고
$\therefore\;[\triangle{ADE} 둘레]\;=\overline{AB}+\overline{AC}\tag{1}$ - 접선의 길이에 대한 성질을 적용하면
$\overline{AP}=x,\;\overline{BP}=y,\;\overline{CR}=z$ 라두면
$\overline{AP}=\overline{AR}=2\sqrt2\;(\because피타고라스)$
$\overline{BP}=\overline{BQ}=y,\;\overline{CR}=\overline{CQ}=z$
$\therefore\; [\triangle{ABC} 둘레]=4\sqrt2+2y+2z\tag{2}$ - 삼각형의 넓이, 둘레 내접원 반지름 사이 관계
$\triangle{ABC}$
$=\dfrac{1}{2}\times[\triangle{ABC}\;둘레]\times\;[내접원의 반지름]$
$=\dfrac{1}{2}\times(4\sqrt2+2y+2z)\times1=5\sqrt2\;(\because (2))$
$\therefore\;y+z=3\sqrt2 \tag{3}$ - (1), (3) 식정리
$[\triangle{ADE} 둘레]=\overline{AB}+\overline{AC}$
$=2x+y+z$
$=4\sqrt2+3\sqrt2=7\sqrt2 \;(\because\;(3))$
ㄷ. $\overline{DE}=2\sqrt2$ (거짓)
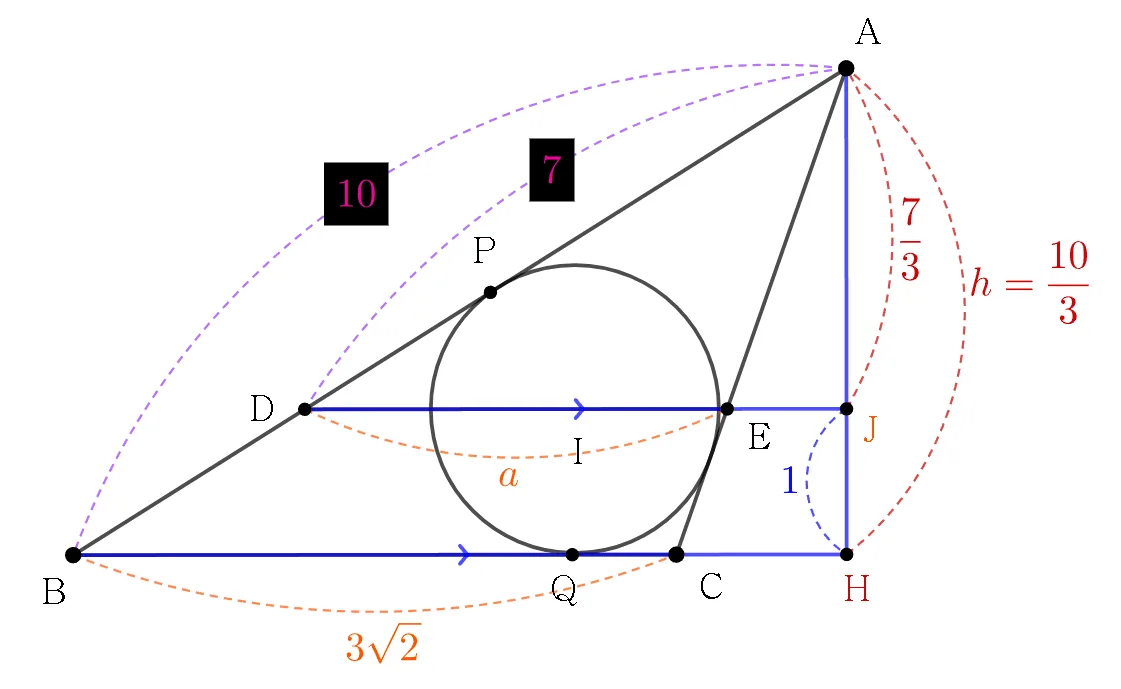
- $\triangle{ABC}=5\sqrt2$이므로
$\overline{AH}=\dfrac{10}{3}$이고
$\overline{AJ}=\dfrac{7}{3}\;(\because\;\overline{HJ}=1)$ - $\triangle{ADJ}\sm\triangle{ABH}$
$\overline{AD}:\overline{AB}=7:10$ - $\triangle{ADE}\sm\triangle{ABC}$
$\overline{AD}:\overline{AB}=\overline{DE}:\overline{BC}$
$a:3\sqrt2=7:10$
$\therefore\; a=\dfrac{21}{10}\sqrt2$
