이번 시간에는 2022년 3월 고1 모의고사 수학 객관식 19, 20, 21번 풀이에 대해 살펴보려 한다. 전체 문제풀이를 원한다면 아래의 파일을 다운로드 하여 풀어보길 바란다. 단답형 29, 30번의 풀이는 글 마지막 부분의 링크를 참고하길 바란다.
다운로드
목차
2022. 3. 고1 모의고사 19번
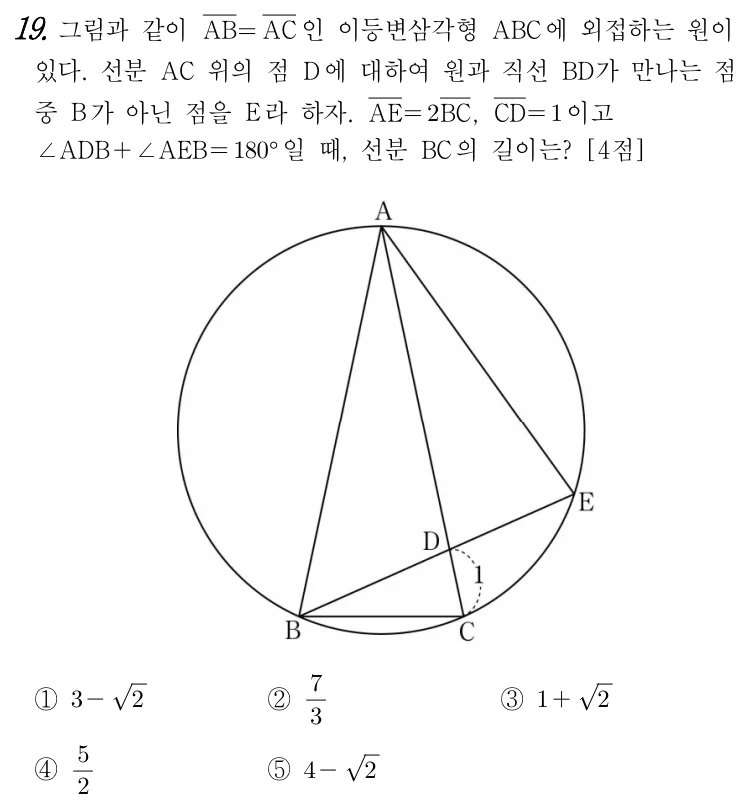
풀이
1단계: 같은 크기 각 찾기
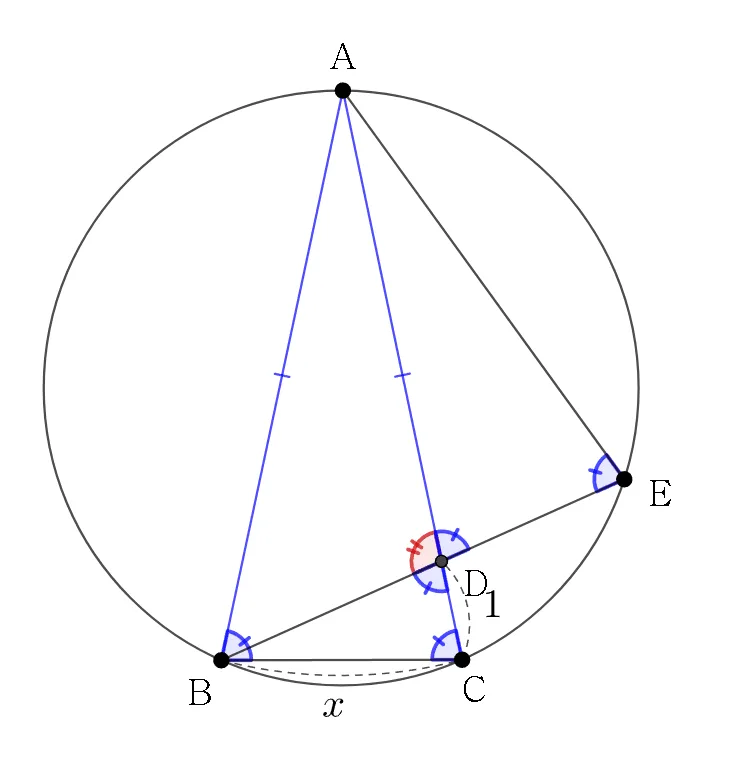
$\angle{ABC}=\angle{ACB} \; (\because\;\overline{AB}=\overline{AC})$
$\angle{ACB}=\angle{AEB}\;(\because\;원주각)$
$\angle{AED}=\angle{ADE}\;(\because\;\angle{AED}+\angle{ADB}=180^{\circ})$
$\angle{ADE}=\angle{BDC}\;\because\;맞꼭지각)$
$\triangle{ABC}\sm\triangle{BCD}\sm\triangle{ADE}$
2단계: 닮음비를 이용해 $\overline{BC}$구하기
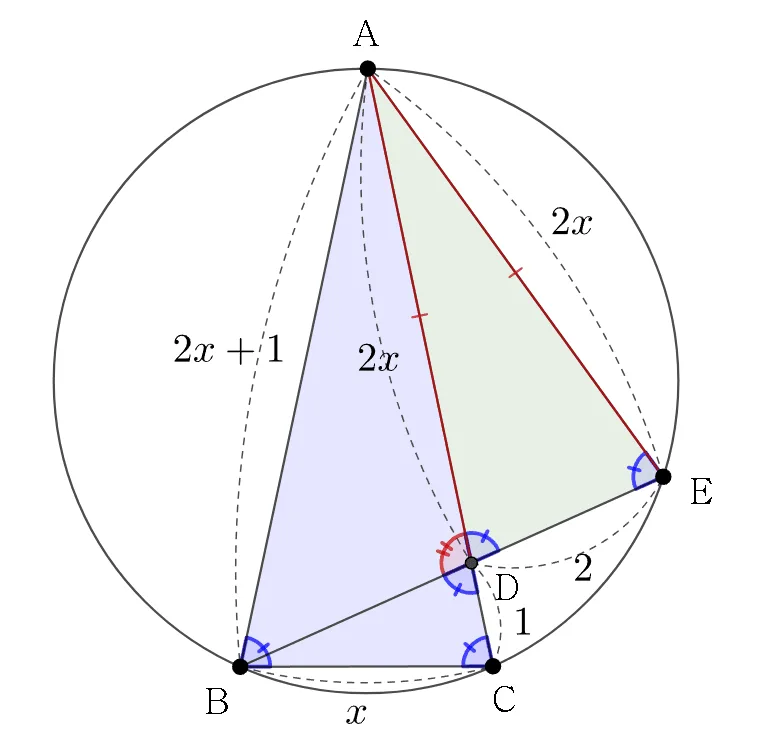
$\overline{BC}=x$라 하면.
$\overline{AE}=2x,\;\overline{DE}=2\;(\because\;\triangle{DBC}\sm\triangle{DAE})$
$\overline{AD}=\overline{AE}=2x,\;\overline{AB}=2x+1$
$2x+1:x=2x:2\;(\because\;\triangle{ABC}\sm\triangle{ADE})$
$2x^2=2(2x+1)$
$x^2-2x-1=0$
$x=+1\pm\sqrt{2}$
$\therefore\;x=+1+\sqrt{2}\;(\because\;x>0)$
2022. 3. 고1 모의고사 20번
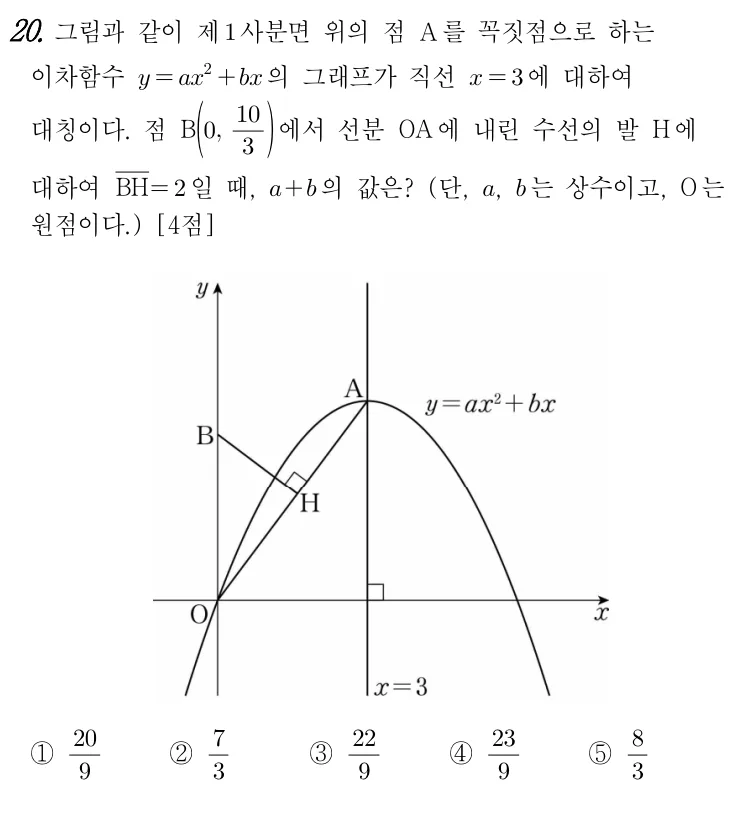
풀이
1단계
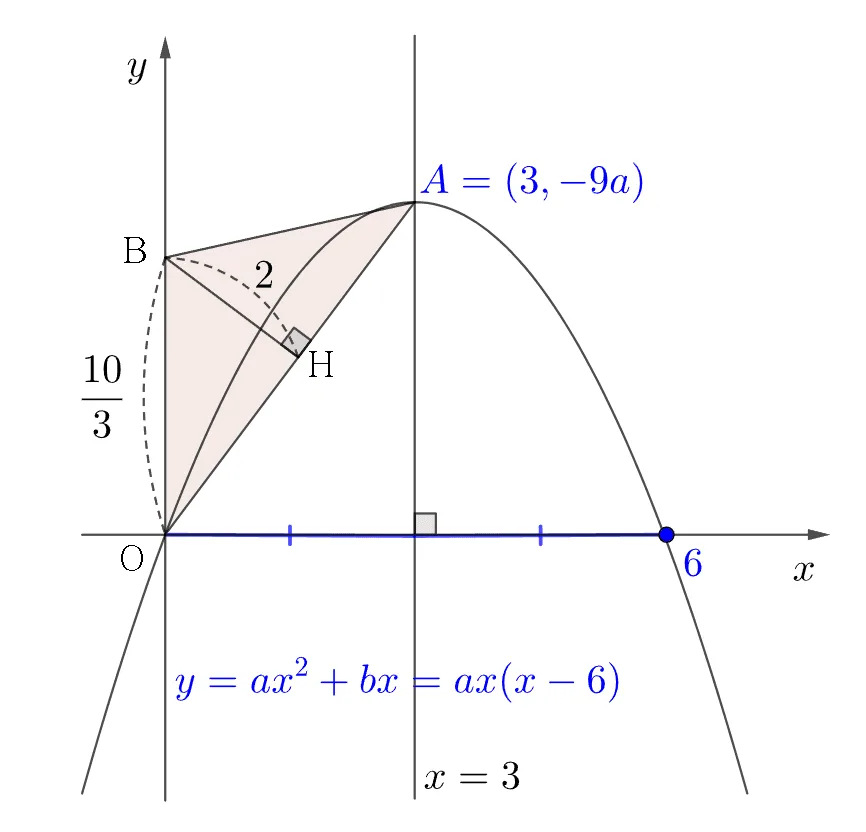
$y=ax^2+bx$은
$x$축과 $(0,0)\;(6,0)$ 만난다.
$y=ax^2+bx=ax(x-6)\;\;\tag{1}$
$[A좌표]\;:\; x=3\; 일때 \; y=3a(3-6)\;\Rightarrow\; (3,-9a)$
2단계 삼각형의 넓이
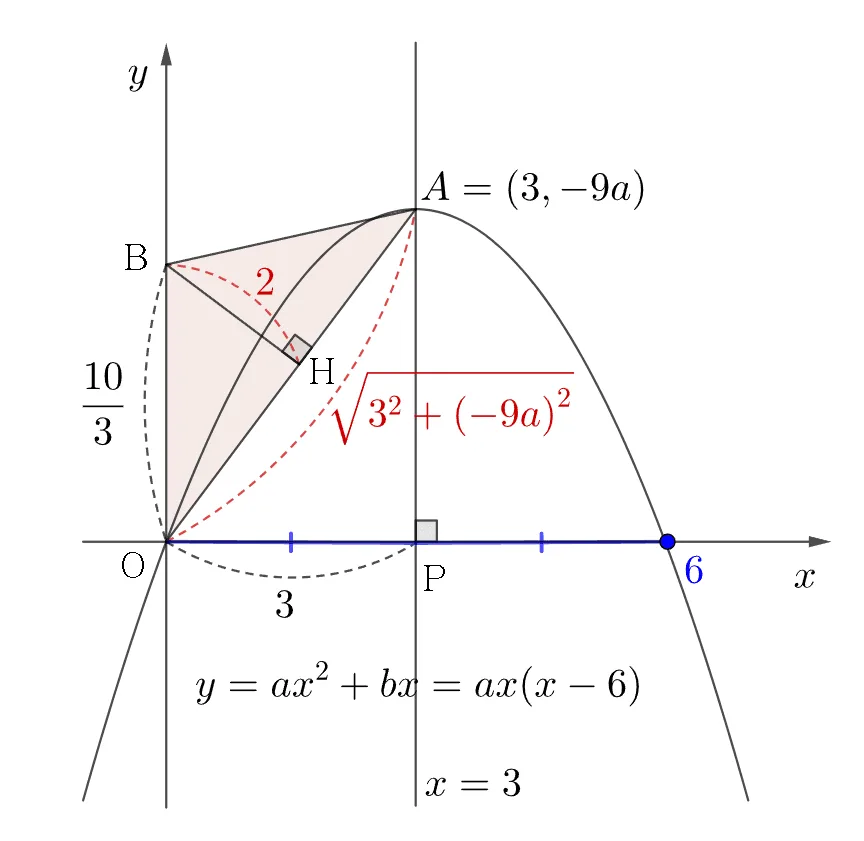
$\triangle{ABO}$넓이
$\dfrac{1}{2}\overline{AO}\times\overline{BH}=\dfrac{1}{2}\overline{BO}\times\overline{OP}$
$\dfrac{1}{2}\times2\times\sqrt{9-81a^2}=\dfrac{1}{2}\times\dfrac{10}{3}\times3$
$9+81a^2=25$
$a=\pm\dfrac{4}{9}\;\rightarrow\; a=-\dfrac{4}{9} \;\;(\because \;a<0)$
식(1) 에 $a=-\dfrac{4}{9}$ 대입
$-\dfrac{4}{9}x(x-6)=-\dfrac{4}{9}x^2+\dfrac{24}{9}$
$b=\dfrac{24}{9}$
$\therefore\;a+b=-\dfrac{4}{9}+\dfrac{24}{9}=\dfrac{20}{9}$
2022. 3. 고1 모의고사 21번
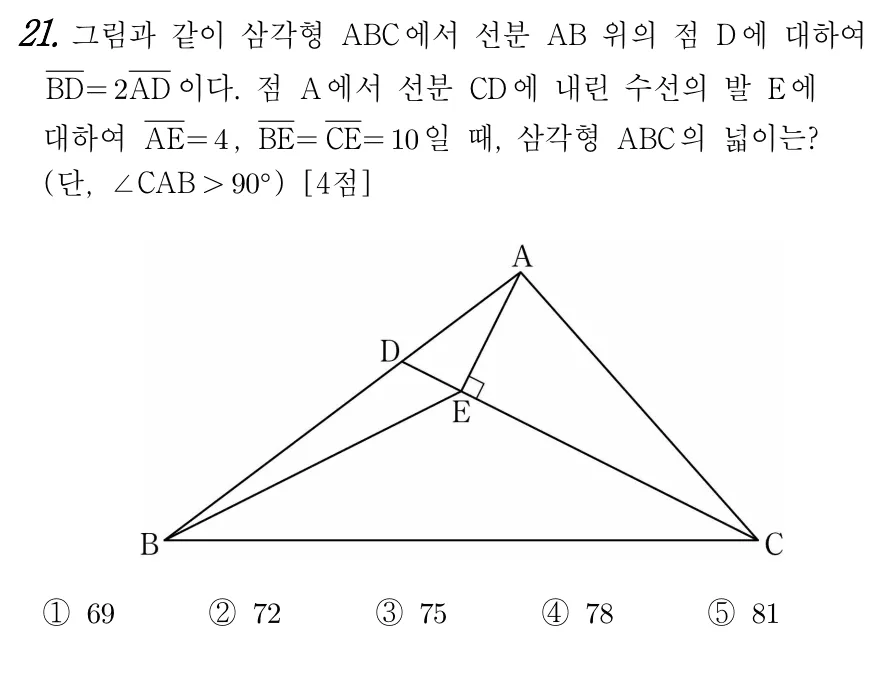
풀이
1단계 : 넓이비 $\rightarrow$ 높이비 $\rightarrow$ 보조선 $\overleftrightarrow{CE}$ 그리기
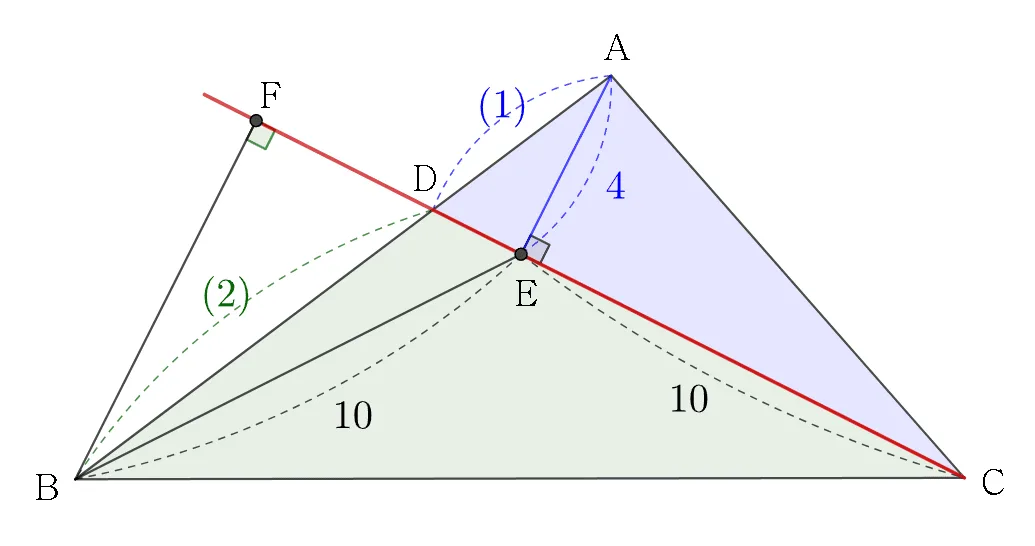
$F$ : $B$ 에서 $\overline{CD}$의 연장선에 내린 수선의 발
$\overline{BF}$//$\overline{AE}$ 이고
$\triangle{DAE}\sm\triangle{DBF}$이다.
$\overline {AD}:\overline{BD}=1:2$ 이므로
$\overline{AE}:\overline{BF}=1:2$ 이고 $\therefore\; \overline{BF}=8$
2단계 :
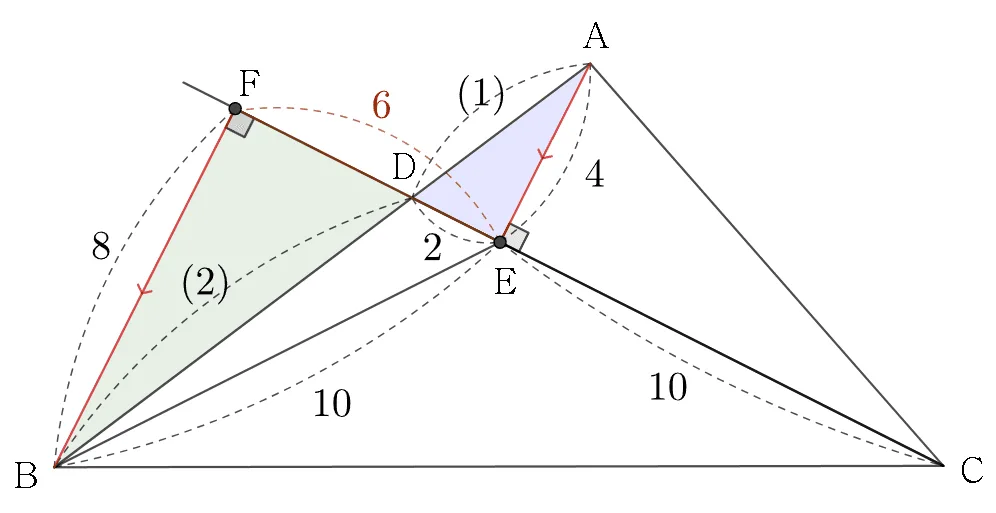
$\triangle{DBF}\sm\triangle{DAE}$이고 닮음비는 2:1이다.
$\overline{EF}=6\;(\because\; 피타고라스 정리)$ 이고
$\overline{DE}=6\times\dfrac{1}{3}=2\;(\because\;비례배분)$ 이다.
$\triangle{ADC}=\dfrac{1}{2}\times\overline{CD}\times \overline{AE}=\dfrac{1}{2}\times 12\times4=24$
$\triangle{BDC}=\dfrac{1}{2}\times\overline{CD}\times \overline{BF}=\dfrac{1}{2}\times 12\times8=48$
$\therefore\;\triangle{ABC}=72$
