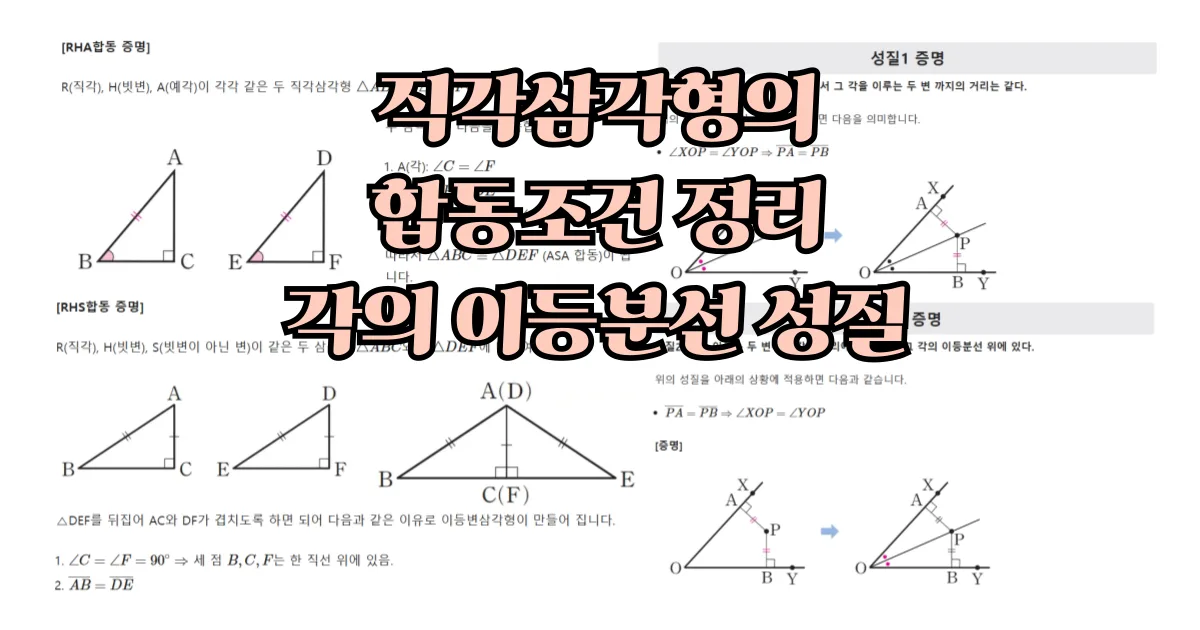
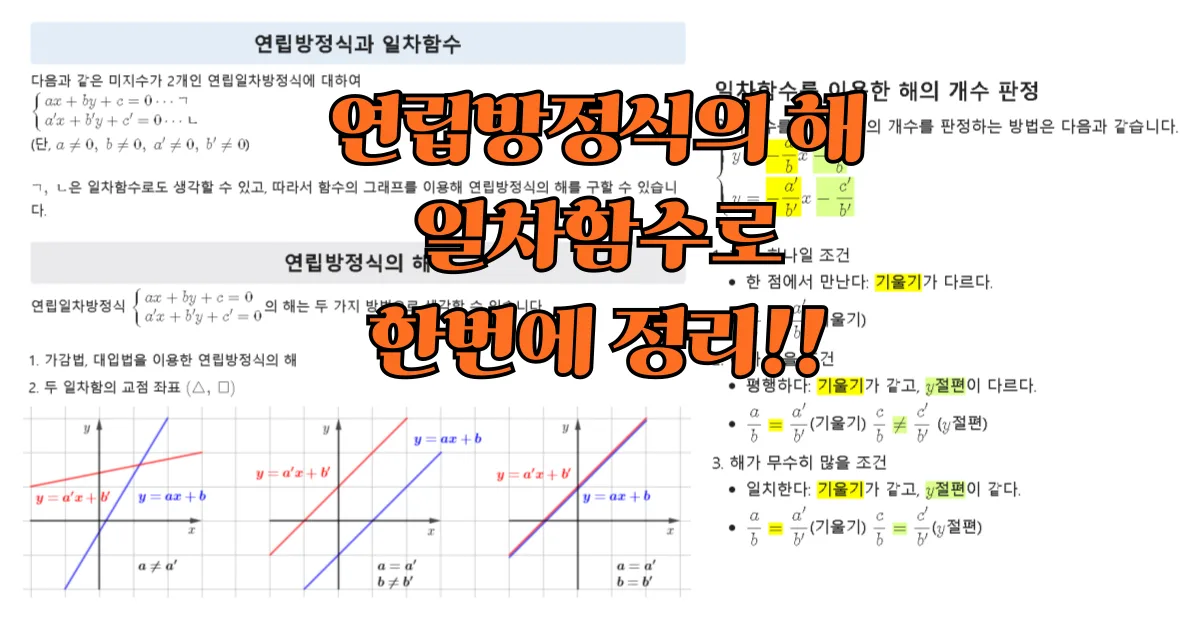
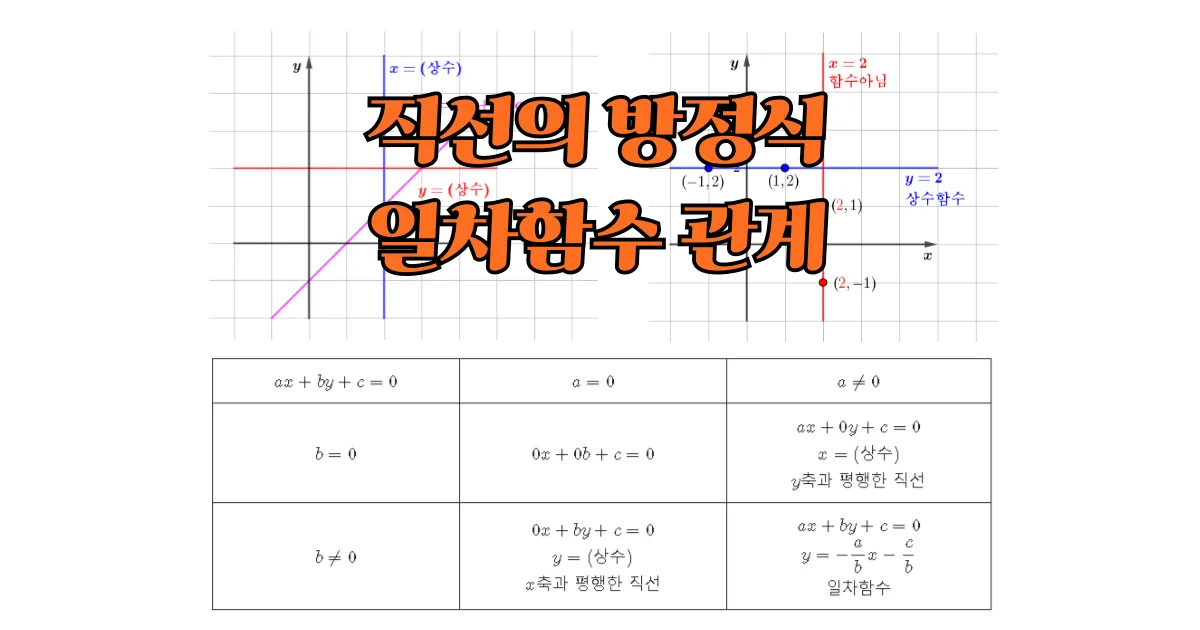
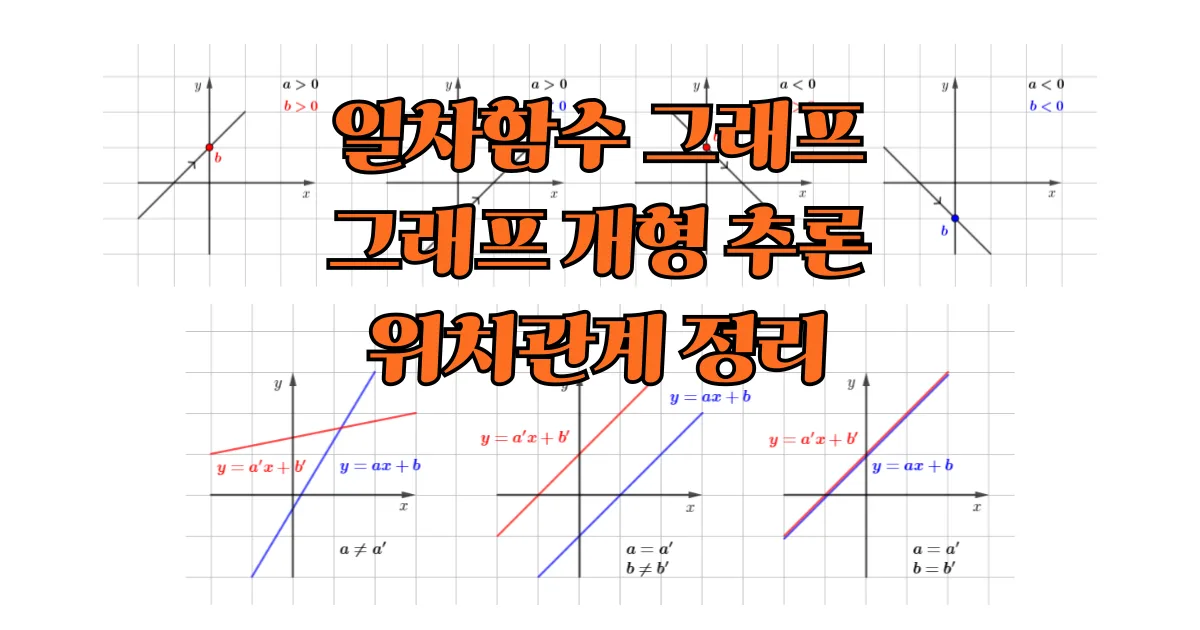
삼각형의 내심의 성질 완벽 정리 (개념, 위치)
이번 시간에는 삼각형의 내심의 성질과 위치에 대해 정리해 보았습니다. 내심은 단순히 내접원의 중심이라는 개념을 넘어, 원의 접점, 각의 이등분선, 삼각형의 대칭성을 포함하고 있는 삼각형의 핵심 개념입니다. 이 글에서는 원의 접선과 접점의 성질부터 출발해, 삼각형의 내심의 정의, 성질, 위치까지 체계적으로 정리했습니다. 복잡해 보일 수 있는 내용을 수학적 원리와 논리적 흐름에 따라 하나씩 연결해 나가며, 마치 퍼즐을 … 더 읽기