도형은 흔하게 접할 수 있는 요소이지만 수학에서 다루는 도형은 일상에서 이야기하는 것과 다르다. 매우 추상화된 도형의 개념을 기본 요소인 점 선 면 부터 시작해 정확히 정리해 보기로 하자. 이번 시간에는 기본요소와 교점과 교선, 평면도형과 입체도형에 대한 복습으로 진행하도록 하겠다.
개요
도형의 기본 요소
도형은 점 선 면으로 구성되고 이를 도형의 기본 요소라고 부른다.
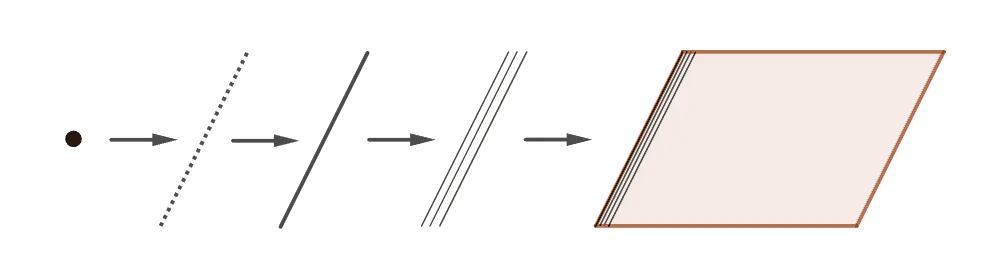
점
수학에서 점은 $\bbox[#ffff00]{\text{위치만 있고 크기와 형태가 없는 도형}}$을 의미하고 다음과 같은 성질을 가지고 있다.
- 길이를 잴 수 없음
- 넓이를 구할 수 없음
- 위치만 존재함
일상에서 점은 수학에서 말하는 점이 아니다. 수학에서 점은 위치만 있고 형태가 없는 추상적인 표현이다. 따라서 길이와 넓이도 논할 수 없다.
선
수학에서의 선은 $\bbox[#ffff00]{\text{점이 지나간 자리}}$로 정의하고 선에는 직선과 곡석이 있다. 선의 성질을 정리하면 다음과 같다.
- 순수한 길이만 가진 도형
- 폭이 없어 넓이가 없음
일상의 선은 폭이 있어 눈에 보이지만 수학에서 선은 폭이 없고 길이만 갖는 도형으로 점과 마찬 가지로 눈으로 볼 수 없는 추상적인 도형이다. 따라서 선의 넓이는 논할 수 없다.
면
수학에서 면은 $\bbox[#ffff00]{\text{선이 연속하여 움직인 자리}}$를 의미한다. 면은 평면, 곡면을 모두 포함하는 개념이다. 면의 성질을 정리하면 다음과 같다.
- 길이와 넓이를 모두 구할수 있음.
- 어떤 두 점을 택해도 연결하는 선을 면 위에 그릴 수 있음.
두 번째 성질은 고립된 점이나 직선을 포함 할 수 없음을 의미한다.
점, 선, 면이 모이면 교선과 교점이 생겨 다양한 모양의 도형이 되기 때문에 이들을 $\bbox[#ffff00]{\text{도형의 기본 요소}}$라고 부른다. 도형의 기본 요소로 만들 수 있는 도형에 대해 살펴보기로 하자.
교점과 교선
선, 면이 서로 만나면 새로운 점과 선을 만들고 이 때 만들어진 점과 선을 각 각 교점, 교선 이라 한다.
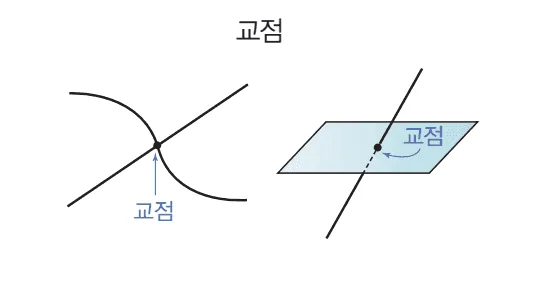
교점
교점은 다음의 상황에서 만들어진다.
- 선과 선이 만날 때
- 선과 면이 만날 때
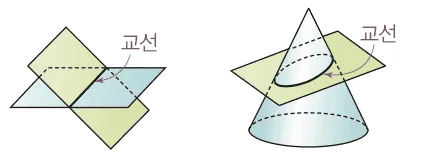
교선
교선은 다음의 상황에서 만들어진다.
- 면과 면이 만날 때
평면도형과 입체도형 (초등)
도형은 크게 평면도형과 입체도형으로 나누어 진다. 예를 통해 간단히 정리하고 넘어가자.
평면도형
평면도형의 정의와 예를 정리하면 다음과 같다.
- 한 평면위에 나타낼 수 있는 도형
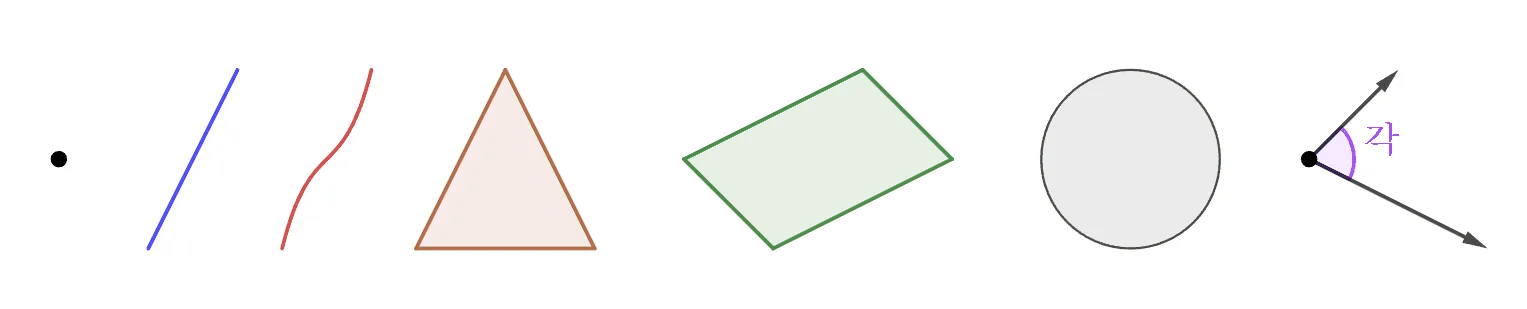
앞으로 배울 ‘각’ 또한 평면에 나타낼 수 있기 때문에 평면도형으로 분류 됨을 미리 정리해 두기로 하자.
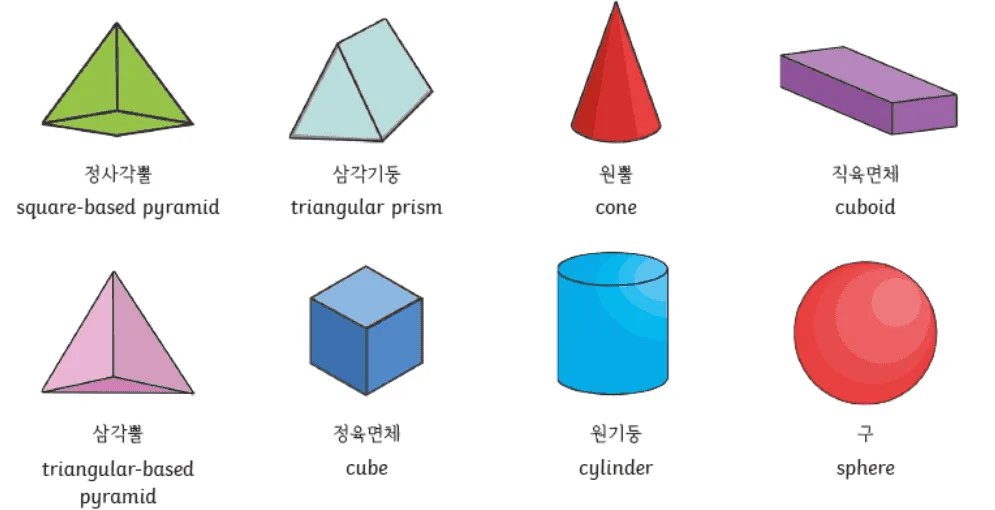
입체도형
이어서 입체도형의 정의와 예시를 정리해보자.
- 한 평면위에 나타낼 수 없는 도형
맺음말
도형의 기본 요소인 점, 선, 면은 수학적 개념의 기초를 이루며, 이들이 어떻게 상호작용하는지 이해하는 것은 도형의 다양한 특성을 파악하는 데 중요하다. 점, 선, 면이 모여 만들어지는 교점과 교선을 이해 하는 것은 이들로 만들어지는 평면도형과 입체도형을 이해는데 기본이 된다.