삼각형의 외심은 중학교 도형 단원에서 반드시 짚고 넘어가야 할 핵심 개념입니다.
단순히 ‘외접원의 중심’이라는 용어로 그치지 않고, 외심의 성질, 구하는 방법, 위치에 따른 특징, 그리고 중3 원주각 개념까지 연결되는 응용은 시험 문제뿐 아니라 수학적 사고력을 기르는 데 필수적인 요소입니다.
이 글에서는 단순한 정의나 공식 나열이 아니라, 외심을 어떻게 구하고, 왜 그렇게 되는지, 그리고 어디에 활용되는지까지 단계별로 안내합니다. 예각, 직각, 둔각 삼각형에서 외심이 어디에 위치하는지를 직관적으로 이해 할 수 있도록 자료를 구성했습니다.
목차
다각형의 외심
먼저 외심이 무엇인지에 대해 정리해 봅시다.
한 다각형의 모든 꼭짓점이 원 위에 있을 때, 그 원은 다각형에 외접한다고 하며, 이 원을 외접원, 그 중심을 외심이라 합니다. 삼각형의 외심은 외접원의 중심이며, 보통 $O$로 나타냅니다.
- 다각형의 외접원: 다각형의 모든 꼭짓점을 동시에 지나는 원
- 다각형의 외심: 외접원의 중심
따라서 삼각형의 외심은 다음과 같이 정의 합니다.
- 삼각형의 외심: 삼각형의 모든 꼭짓점을 동시에 지나는 외접원의 중심
삼각형의 외심의 성질
$O$가 삼각형$\triangle{ABC}$의 외심이라면 다음과 같은 성질을 만족합니다.
- 성질1: 외심에서 세 꼭짓점에 이르는 거리는 반지름으로 같다.
- $\overline{OA} = \overline{OB} = \overline{OC}=R(\text{반지름})$
- 성질2: 외심에서 세 변에 내린 수선은 세 변의 수직이등분선이다.
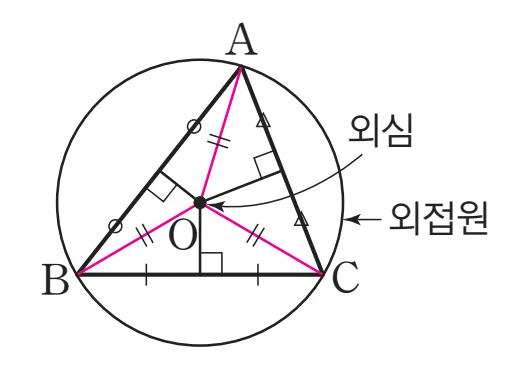
$O$가 $\triangle{ABC}$의 외심이라면 $O$에서 세 꼭짓점까지 거리는 반지름($R$)으로 같게 됩니다. 따라서 [성질1]은 당연히 성립합니다.
[성질2 증명]
외심에서 세 변에 내린 수선은 세 변의 수직이등분선임을(성질2)은 아래와 같이 증명할 수 있습니다.
$O$가 삼각형 $\triangle{ABC}$의 외심이면 [성질1]에 의해 다음이 성립합니다.
- $\triangle{OAB}$, $\triangle{OBC}$, $\triangle{OCA}$: 이등변 삼각형
따라서 $O$에서 세 변에 내린 수선은 세 변의 수직이등분선이됩니다.
삼각형의 외심을 찾는 방법
다음 두 상황에 대해 생각해 보면서 외심의 존재성에 대해 생각해 봅시다.
- 외심이 주어진 경우: $O$가 삼각형의 외심으로 주어지는 경우 위의 두 성질을 만족
- 외심이 주어지지 않은 경우: 외심이 항상 존재하는지? 외심을 찾는 방법?
외심이 항상 존재하고 다음과 같이 찾을 수 있음이 알려져 있습니다.
- 삼각형의 세 변의 수직이등분선은 한 점 에서 만나고 이 점은 외심이 된다.
외심의 존재성에 대한 증명
- 삼각형의 세 변의 수직이등분선은 한 점 에서 만나고 이 점은 외심이 된다.
[증명]
$\triangle{ABC}$에서 $\overline{AB}$와 $\overline{BC}$의 수직이등분선의 교점이 존재하고 이 점을 $O$라 합시다.
이등변삼각형의 조건에 의해
- $O$는 $\overline{AB}$의 수직이등분선 위에 있으므로 $\triangle{OAB}$는 이등변삼각형이고, $\overline{OA} = {\color{blue}\overline{OB}}$
- $O$는 $\overline{BC}$의 수직이등분선 위에 있으므로 $\triangle{OBC}$는 이등변삼각형이고, ${\color{blue}\overline{OB}}= \overline{OC}$
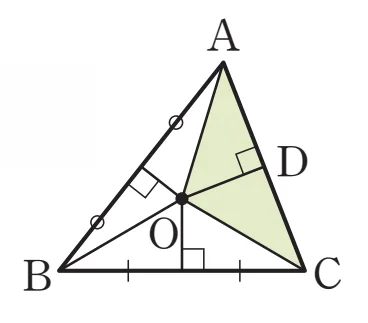
두 사실을 정리하면 $\bbox[#e4ecca]{\overline{OA}} = {\color{blue}\overline{OB}}= \bbox[#e4ecca]{\overline{OC}}$이고 $\bbox[#e4ecca]{\triangle{AOC}}$는 이등변 삼각형입니다. 따라서 다음이 성립합니다.
- $\overline{AC}$의 수직이등분선은 $O$를 지난다.
세 변의 수직이등분선이 모두 한 점$O$에서 만나고 (존재성) 다음과 같은 이유로 이 점은 외심이 됩니다.
- 중심이 $O$ 반지름이 $\overline{OA} = \overline{OB} = \overline{OC}=R(\text{반지름})$인 원을 그리면, 이 원은 $\triangle{ABC}$의 세 꼭짓점을 지나는 외접원이 되고, 점$O$는 $\triangle{ABC}$의 외심이 됩니다.
삼각형의 외심의 응용
응용1
점 $O$가 $\triangle ABC$의 외심일 때, 다음이 성립합니다.
- $\angle x + \angle y + \angle z = 90^\circ$
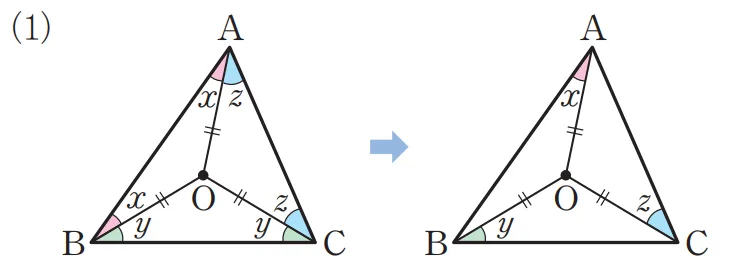
[증명]
$O$는 $\triangle ABC$의 외심이므로 다음을 만족합니다.
- $\overline{OA} = \overline{OB} = \overline{OC}$
- $\triangle{OAB}$, $\triangle{OBC}$, $\triangle{OCA}$: 이등변삼각형
따라서 삼각형의 세 각을 $x,\;y,\;z$를 이용해 다음과 같이 표현할 수 있습니다.
$\begin{align}\angle BAC& + \angle ABC + \angle ACB \\
&= 2(\angle x + \angle y + \angle z)\\
&=180^\circ \end{align}$
따라서 $\angle x + \angle y + \angle z = 90^\circ$를 만족합니다.
응용2
점 $O$가 $\triangle ABC$의 외심일 때, 다음이 성립합니다.
- $\angle{BOC} = 2 \angle{BAC}$
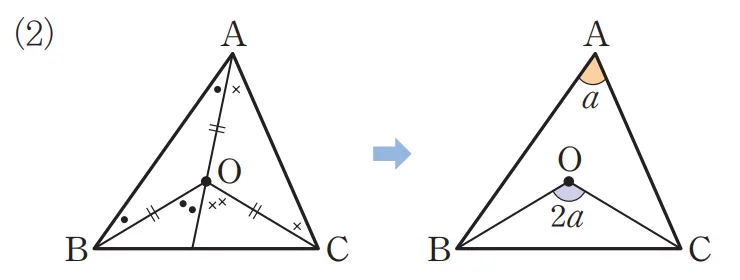
[증명]
$\overline{AO}$의 연장선과 $\overline{BC}$가 만나는 교점을 $D$라고 두고,
$\angle{OAB} = \angle{x}$, $\angle{OAC} = \angle{y}$라고 두면 다음이 성립합니다.
$\triangle{OAB}$, $\triangle{OAC}$: 이등변 삼각형이므로
- $\angle{OAB}=\angle{OBA}=x$
- $\angle{OAC}=\angle{OCA}=y$
삼각형의 외각은 이웃하지 않는 두 내각의 합과 같기 때문에 다음이 성립합니다.
- $\angle{BOD}=x+x=2x$
- $\angle{COD}=y+y=2y$
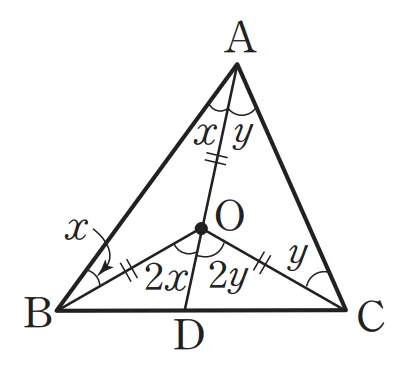
$\angle{BOC}=\angle{BOD}+\angle{COD}=2x+2y$
$\angle{BAC}=x+y$를 이용해 $\angle{BOC}$를 정리하면 다음과 같은 결론을 얻을 수 있습니다.
- $\angle{BOC}=2x+2y=2(x+y)=2\angle{BAC}$
따라서 $\angle{BOC}=2\angle{BAC}$가 성립합니다.
확장
이 사실을 확장하면 다음과 같은 사실을 확인할 수 있습니다. 이는 중학교 2학년에서 외심의 응용으로 다룰 수도 있고, 중학교 3학년 원주각의 활용으로 다룰 수도 있습니다.
$O$는 $\triangle{ABD}$의 외심이므로 $\overparen{BD}$를 포함하는 부채꼴이 중심각은 $2a$입니다.
$O$는 $\triangle{ABD}$의 외심이기도 하므로 $\overparen{BAD}$를 포함하는 부채꼴의 중심각은 $2c$입니다. (보조선 $\overrightarrow{CO}$를 이용해 삼각형의 외각성질 이용)
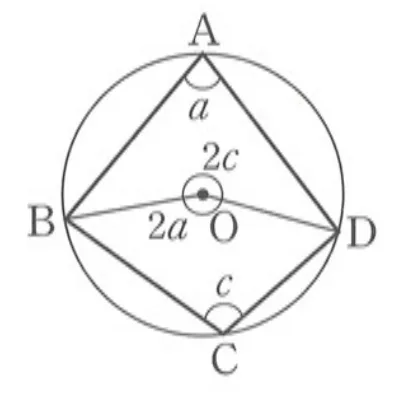
따라서 $2a+2c=360^\circ$이고 $a+c=180^\circ$입니다. 이를 통해 원에 내접하는 사각형의 성질을 다음과 같이 정리할 수 있습니다.
- 원에 내접하는 사각형의 성질: 마주보는 각의 크기합이 $180^\circ$
이 성질은 사각형이 원에 내접할 조건도 됩니다. (중학교 3학년 과정)
삼각형의 외심 위치
예각, 직각, 둔각 삼각형에서 외심을 찾는 과정은 직관적으로 받아들이고, 중학교 3학년 원주각을 학습할 때 증명할 수 있게 됩니다.
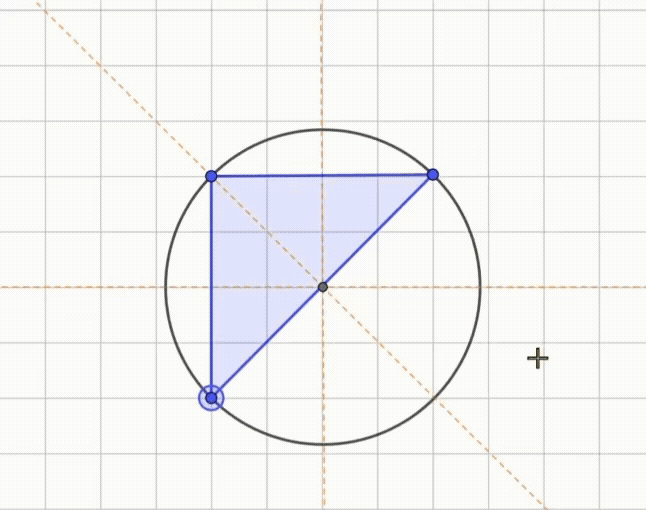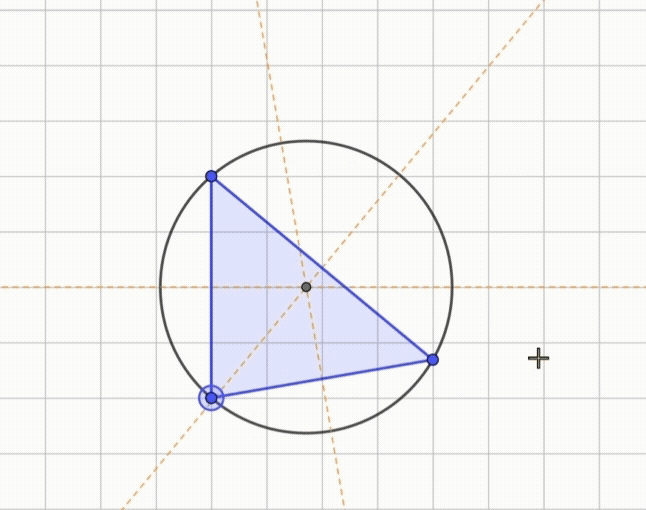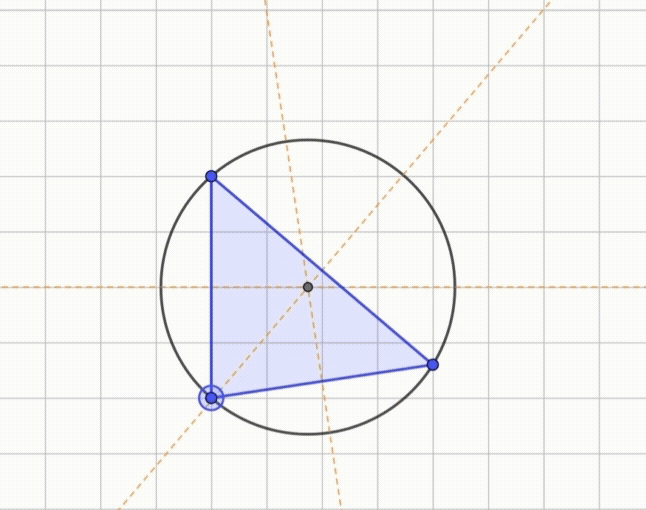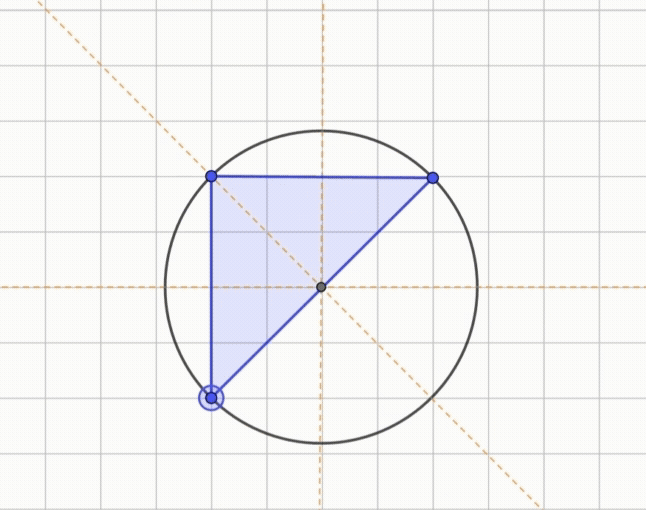
영상속의 결과를 정리하면 다음과 같습니다.
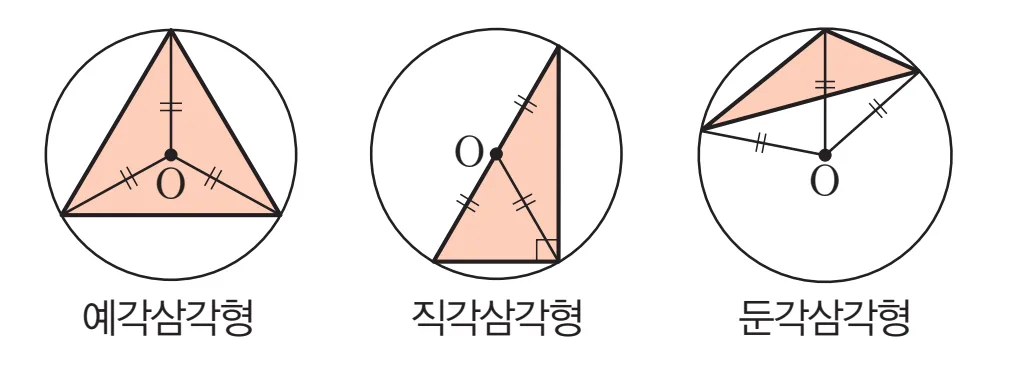
- 예각삼각형: 외심은 삼각형 내부
- 직각삼각형: 외심은 빗변의 중점
- 둔각삼각형: 외심은 삼각형의 외부
여기서 주목할 점은 직각삼각형의 외심은 빗변의 중점이 되고 따라서 다음이 성립합니다.
- (직각삼각형의 외접원 반지름)$=\dfrac{(\text{빗변의 길이})}{2}$
추가로 이등변삼각형에서 외심은 다음과 같이 정리할 수 있습니다.
- 이등변삼각형의 외심은 꼭지각의 이등분선 위에 있다.
