수학에서 삼각형의 합동은 기하의 출발점이자 핵심 개념입니다. 특히 직각삼각형은 자주 등장하기 때문에, 그 합동 조건을 정확하게 이해하는 것이 중요합니다.
본문에서는 직각삼각형의 합동조건인 RHA 합동과 RHS 합동을 영어 용어와 이니셜 의미까지 곁들여 정리하였습니다. 뿐만 아니라 각의 이등분선 성질까지 개념과 증명으로 나누어 구성했습니다.
단순한 공식 암기가 아닌 논리적인 이해를 목표로 구성하였으며, 중학생은 물론 수능 기초 개념을 다시 다지고 싶은 학습자에게도 도움이 될 수 있도록 구성했습니다. 이 글 하나로 직각삼각형 합동과 각의 이등분선 개념을 확실히 정리해보세요!
직각삼각형의 합동조건
직각삼각형의 합동조건에서 직각, 빗변, 각을 표현하는 방법을 정리하고 이를 이용해 합동조건을 정리해 봅시다.
| 한글 명칭 | 영어 표현 | 이니셜 | 직각삼각형의 합동 조건 |
|---|---|---|---|
| 직각 | Right angle | R | 90도인 각 |
| 빗변 | Hypotenuse | H | 직각의 대변 가장 긴 변 |
| 각 | Angle | A | 예각 |
| 변 | Side | S | 빗변 이외의 변 |
일반 삼각형의 합동조건에 대한 내용이 기억나지 않는다면 아래의 링크를 통해 학습하길 바랍니다.
지금부터 학습 할 직각삼각형의 합동조건은 다음과 같습니다.
- RHA 합동
- RHS 합동
RHA 합동
RHA합동이란 다음 조건을 만족하는 두 삼각형의 합동조건입니다.
- R(직각), H(빗변), A(예각)이 각각 같다.
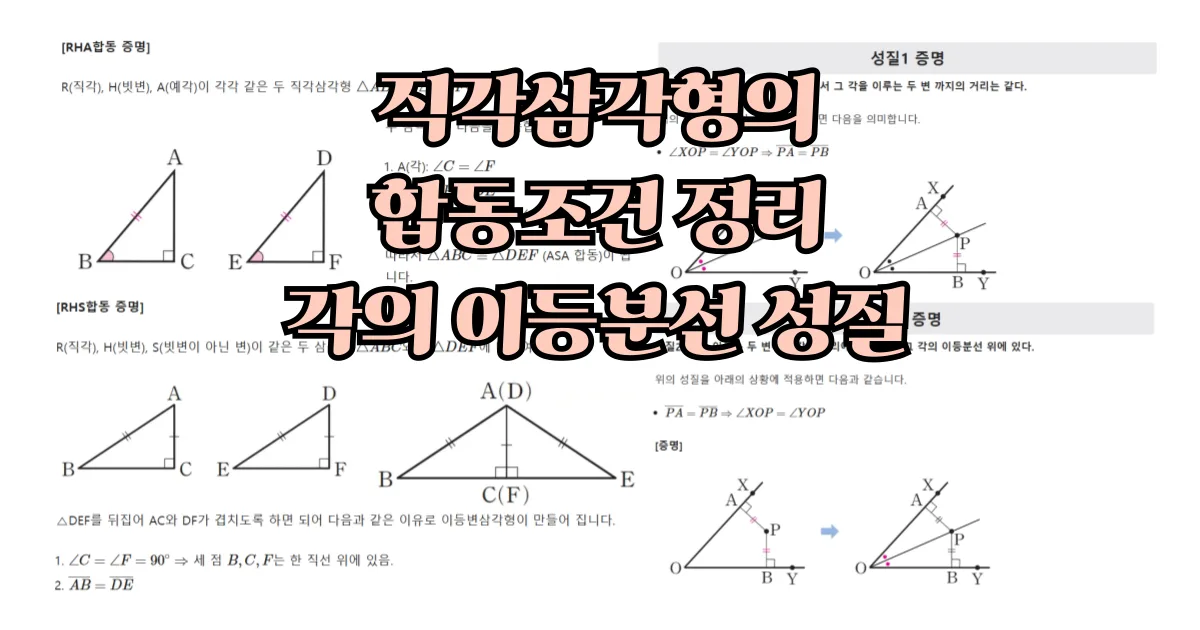
[RHA합동 증명]
R(직각), H(빗변), A(예각)이 각각 같은 두 직각삼각형 $\triangle{ABC}$와 $\triangle{DEF}$에 대하여
두 삼각형은 다음을 만족합니다.
- A(각): $\angle C = \angle F$
- S(변): $\overline{AB} = \overline{DE}$
- A(각): $\angle B = \angle E$ $\Rightarrow \angle A = \angle D$
따라서 $\triangle ABC \equiv \triangle DEF$ (ASA 합동)이 됩니다.
매번 이렇게 직각삼각형의 합동을 ASA로 판정하는 것이 번거롭기 때문에,
앞으로 다음 조건을 만족하는 두 직각삼각형을 RHA합동으로 판정하기로 합시다.
- R(직각), H(빗변), A(예각)이 같은 두 직각삼각형
RHS 합동
RHS합동이란 다음 조건을 만족하는 두 삼각형의 합동조건입니다.
- R(직각), H(빗변), S(빗변이 아닌 변)이 각각 같다.
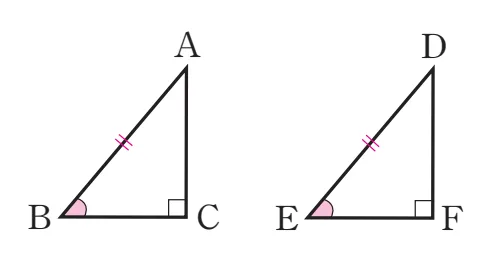
[RHS합동 증명]
R(직각), H(빗변), S(빗변이 아닌 변)이 같은 두 삼각형 $\triangle{ABC}$와 $\triangle{DEF}$에 대하여
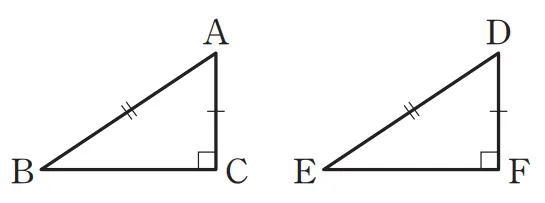
△DEF를 뒤집어 AC와 DF가 겹치도록 하면 되어 다음과 같은 이유로 이등변삼각형이 만들어 집니다.
- $\angle C = \angle F=90^\circ$ $\Rightarrow$ 세 점 $B, C(F), E$는 한 직선 위에 있음.
- $\overline{AB}=\overline{DE}$
따라서 $\triangle{ABE}$는 이등변 삼각형이 됩니다.
- A(각): $\angle B = \angle E$
- S(변): $\overline{AB} = \overline{DE}$
- A(각): $\angle C = \angle F=90^\circ \Rightarrow \angle A = \angle D$
따라서 $\triangle{ABC} \equiv \triangle{DEF}$ (ASA 합동)이 됩니다.
매번 이렇게 직각삼각형의 합동을 ASA로 판정하는 것이 번거롭기 때문에,
앞으로 다음 조건을 만족하는 두 직각삼각형을 RHS합동으로 판정하기로 합시다.
- R(직각), H(빗변), S(빗변이 아닌 변)이 각각 같다.
각의 이등분선 성질과 조건
각의 이등분선 위의 점(P)의 성질과 조건은 다음과 같습니다.
- 성질: 각의 이등분선 위의 점 $\Rightarrow$그 각을 이루는 두 변 까지의 거리가 같다.
- 조건: 각을 이루는 두 변에서 같은 거리에 있는 점 $\Rightarrow$ 각의 이등분선 위의 점이다.
각의 이등분선 성질 증명
성질: 각의 이등분선 위의 점 $\Rightarrow$ 각을 이루는 두 변 까지의 거리가 같다.
[증명]
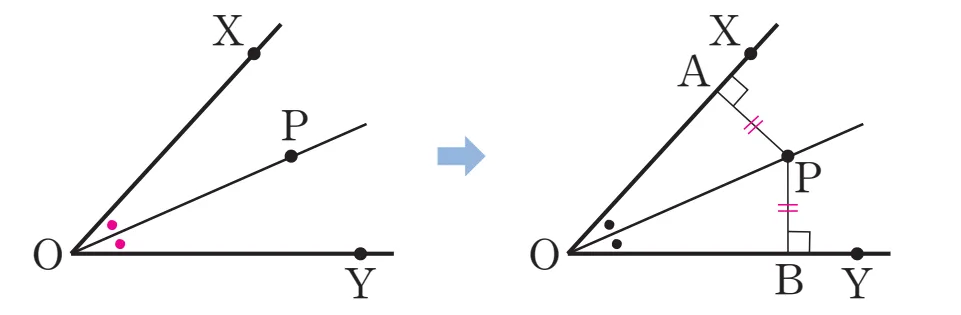
위의 성질을 아래의 그림에 적용하여 다음을 증명하면 충분합니다.
- $\angle{XOP}=\angle{YOP}\Rightarrow\overline{PA}=\overline{PB}$
$\angle{XOY}$의 이등분선위의 점 $P$에서 반직선 $\overrightarrow{OX}$와 $\overrightarrow{OY}$에 내린 수선의 발 $A,\;B$에 대하여 $\triangle{AOP},\;\triangle{BOP}$는 다음을 만족합니다.
- R(직각): $\angle{PAO} = \angle{PBO}$
- H(빗변): $\overline{OP}$는 공통
- A(예각): $\angle{AOP} = \angle{BOP}$
따라서 $\triangle{AOP} \equiv \triangle{BOP}$ (RHA합동)이고 따라서 다음과 같은 결과를 얻을 수 있습니다.
- $\overline{PA} = \overline{PB}$
각의 이등분선 조건 증명
조건: 각을 이루는 두 변에서 같은 거리에 있는 점 $\Rightarrow$ 각의 이등분선 위의 점
[증명]
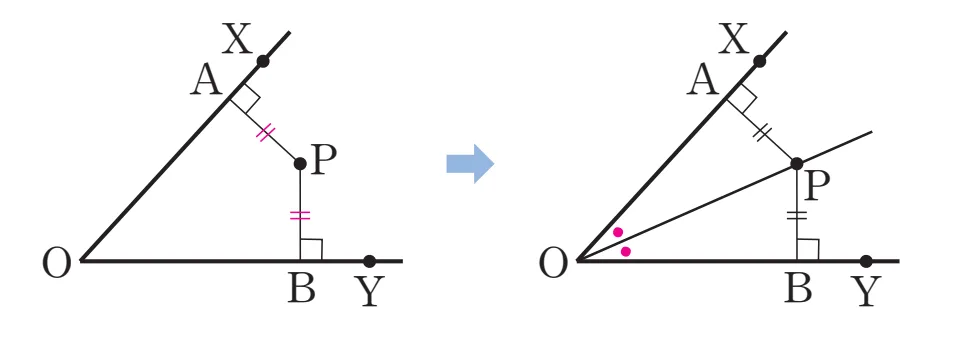
위의 성질을 아래의 그림에 적용하여 다음을 증명하면 충분합니다.
- $\overline{PA} = \overline{PB} \Rightarrow \angle{XOP}=\angle{YOP}$
점 $P$에서 반직선 $\overrightarrow{OX}$와 $\overrightarrow{OY}$에 내린 수선의 발 $A,\;B$에 대하여 $\overline{PA} = \overline{PB}$일 때, $\triangle{AOP},\;\triangle{BOP}$는 다음을 만족합니다.
- R(직각): $\angle{PAO} = \angle{PBO}$
- H(빗변): $\overline{OP}$는 공통
- S(빗변이 아닌 변): $\overline{AP} = \overline{BP}$
따라서 $\triangle{AOP} \equiv \triangle{BOP}$ (RHS합동)이고, 따라서 다음과 같은 결과를 얻을 수 있습니다.
- $\angle{XOP}=\angle{YOP}$