이번 시간에는 2022년 3월 고1 모의고사 수학 단답형 고난이도 문제를 풀어보기로 하자. 2022년 3월 모의고사 문제와 풀이 자료는 아래의 링크를 통해 다운 받아 풀어보고 객관식 고난이도 문제의 풀이는 글 가장 하단에 링크를 남겨 두었으니 참고하길 바란다.
목차
다운로드
2022년 3월 고1 모의고사 29번

풀이
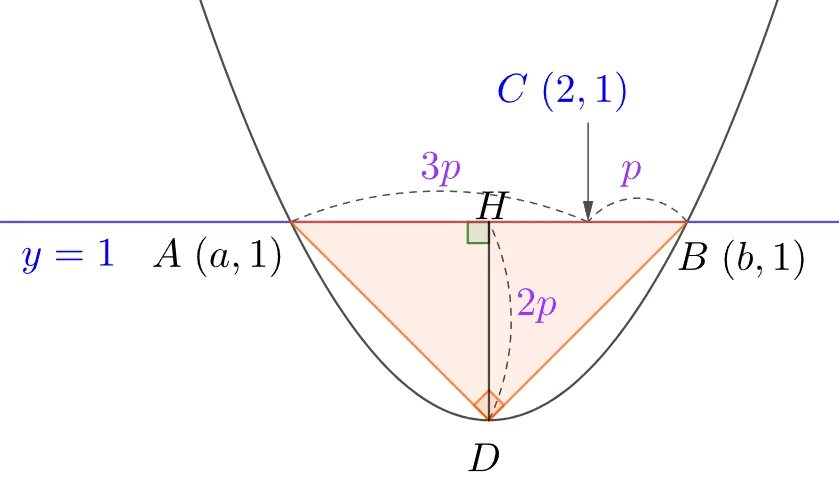
$a<2<b,\;\overline{AC}=3\overline{BC}$ 일 때
$y=1$ 위의 $A(a,1),\;B(b,1),\;C(2,1)$를 표현
$\overline{BC}=p,\;\overline{AC}=3p$라 두면
$\overline{DH}=2p\;(\because\;이등변 삼각형)$
$\triangle{ADB}=\dfrac{1}{2}\times4p\times2p=16$
$p=\pm2\rightarrow p=2\; (\because\; p(길이)>0)$
D의 좌표 $x=2-p=0,\; y=1-2p=-3$
이차함수식 : $f(x)=ax^2-3$
$f(4)=1:\; f(4)=16a-3=1,\; a=\dfrac{1}{4}$
$f(x)=\dfrac{1}{4}x^2-3$
$\therefore\; f(8)=\dfrac{1}{4}\times8^2-3=13$
2022년 3월 고1 모의고사 30번
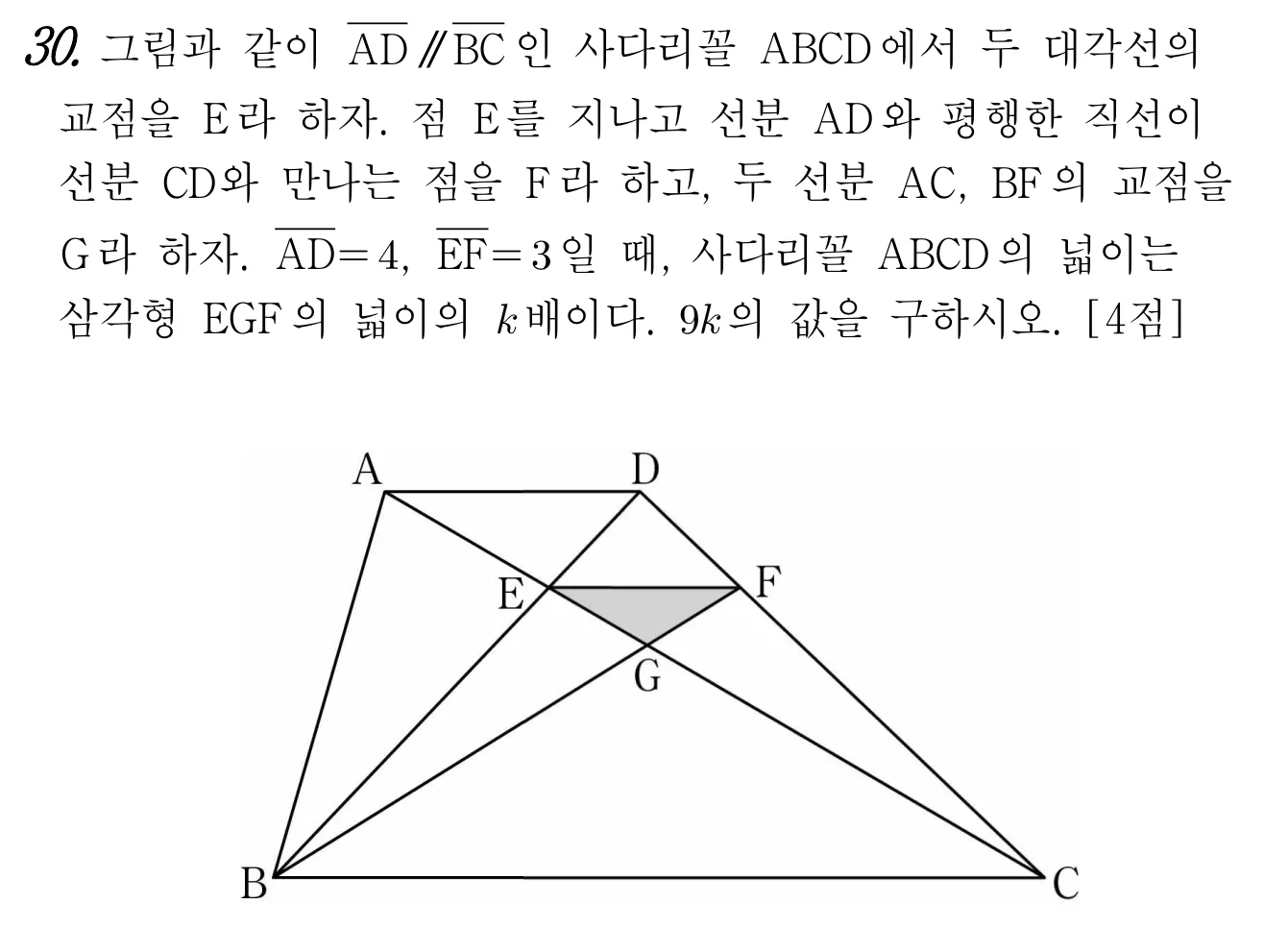
풀이
1단계
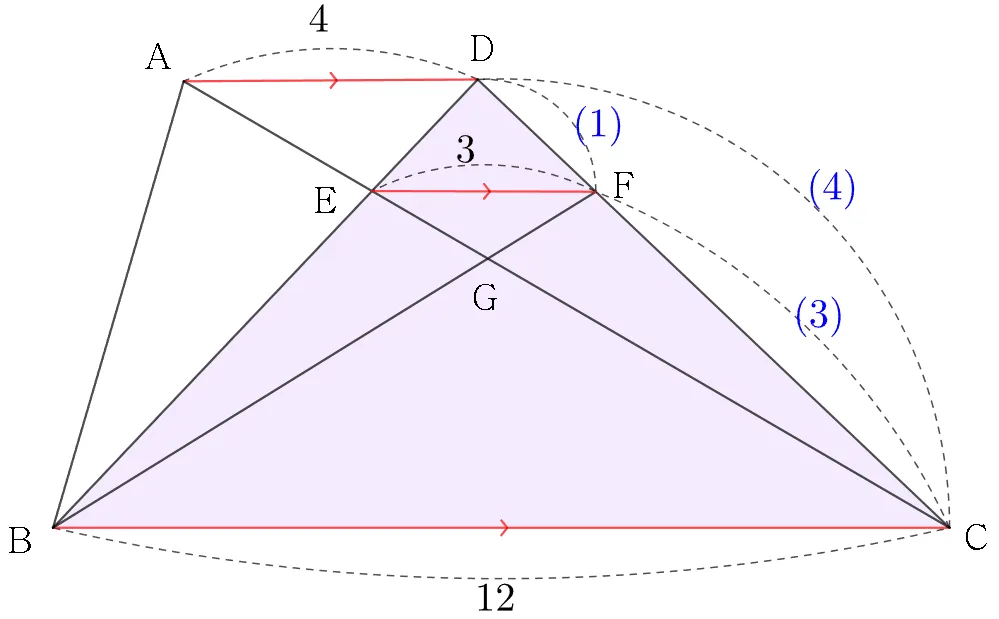
$\triangle{CEF}\sm\triangle{CAD}$ 이므로
$\overline{EF}:\overline{AD}=\overline{CF}:\overline{CD}=3:4$
$\triangle{DEF}\sm\triangle{DBC}$ 이므로
$\overline{EF}:\overline{BC}=\overline{DF}:\overline{DC}=1:4$ 이고
$\overline{BC}=12$이다.
2단계
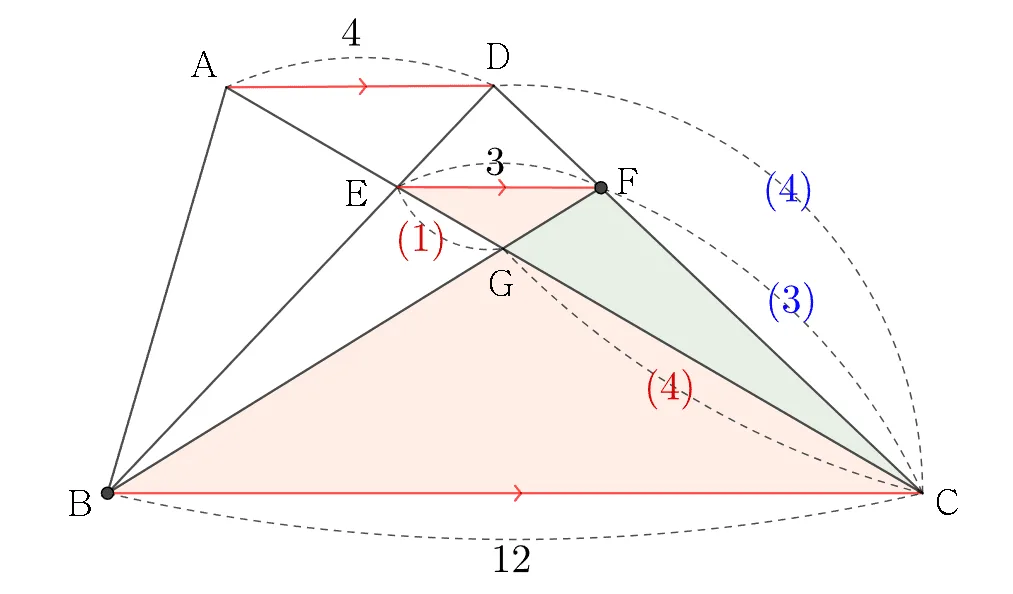
$\triangle{GEF}\sm\triangle{GCB}$ 이므로
$\overline{EG}:\overline{CG}=\overline{EF}:\overline{BC}=1:4$
$\triangle{EGF}:\triangle{FGC}=1:4$ 이다.
$\triangle{EGF}=S$로 두면
$\triangle{FGC}=4S,\; \triangle{CEF}=5S$
$\triangle{CAD}=\triangle{CEF}\times\dfrac{4^2}{3^2}=\dfrac{16}{9}\times5S$
$\triangle{CAB}=\triangle{CAD}\times\dfrac{12}{4}=\dfrac{16}{9}\times5S\times3$
$\square{ABCD}=\dfrac{16}{9}\times20\times S$
$k=\dfrac{16}{9}\times20$
$\therefore\; 9k=320$
