회전체는 평면 도형을 특정 축을 기준으로 회전시켜 생성되는 3차원 도형을 말합니다. 대표적인 회전체로는 구, 원기둥, 원뿔 등이 있으며, 각각의 회전체는 고유한 성질과 특징을 가지고 있습니다. 이 글에서는 회전체의 정의, 종류, 성질, 그리고 전개도에 대해 자세히 설명하였습니다.
목차
회전체의 정의 용어 종류
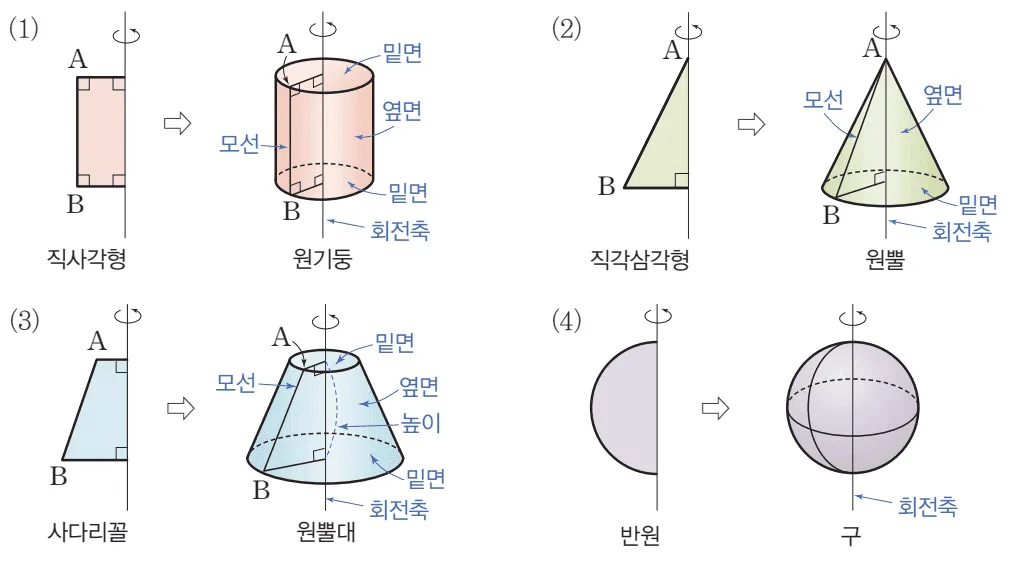
회전체: 평면도형을 한 직선 $l$을 축으로 1회전 시켜 얻은 입체도형
- 회전축 : $l$
- 옆면 : (1), (2), (3)에서 $\overline{AB}$가 회전하여 만들어지는 면
- 옆면은 곡면이다.
- 모선 : 회전체에서 $\colorbox{#ffff00}{옆면}$을 만드는 직선
(1), (2), (3)의 모선: $\overline{AB}$
(4) 구는 옆면이 없고, 따라서 모선도 없다.
회전체의 종류
- 원기둥
- 회전 평면도형 : 직사각형
- 회전축 : 직사각형의 한 변
- 원뿔
- 회전 평면도형 : 직각삼각형
- 회전축 : 직각이 포함된 변
- 원뿔대 : 원뿔을 밑면과 평행한 평면으로 자를 때 원뿔이 아닌 부분
- 회전 평면도형 : 이웃한 각이 직각인 사다리꼴
- 회전축 : 양끝각이 직각인 변
- 구 : 공간에서 한 점으로 부터 같은 거리 떨어진 점들로 이루어진 도형
- 회전 평면도형 : 반원
- 회전축 : 반원의 지름
회전체의 성질
단면
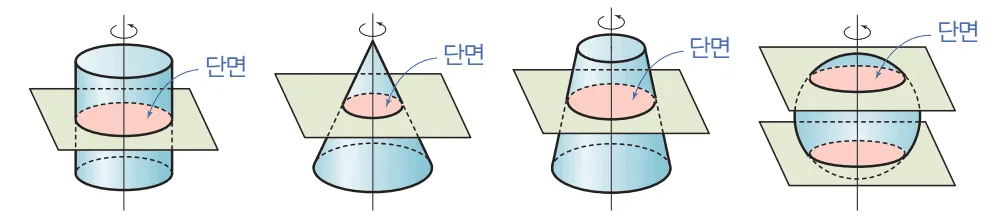
회전축에 수직인 단면
- 회전축에 수직인 단면으로 자를 때 생기는 단면은 항상 $\colorbox{#ffff00}{원}$이다.
회전축을 포함한 단면
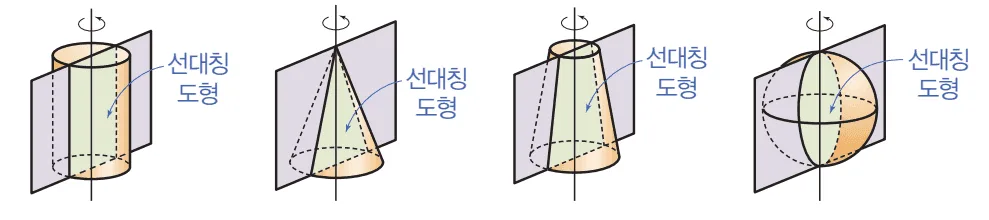
회전축을 포함한 평면으로 자른 단면의 공통 성질
- 회전체를 정면에서 바라본 도형과 같다.
- 서로 합동, 회전축에 선대칭 도형.
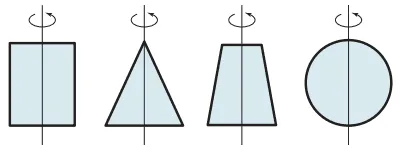
회천축을 포함한 평면으로 자른 단면의 모양
- 원기둥 : 직사각형
- 원뿔 : 이등변삼각형
- 원뿔대 : 등변사다리꼴
- 구 : 원
- 구의 단면은 항상 원이다.
- 가장 큰 단면은 중심을 지나는 평면으로 자른 단면이다.
회전체의 전개도
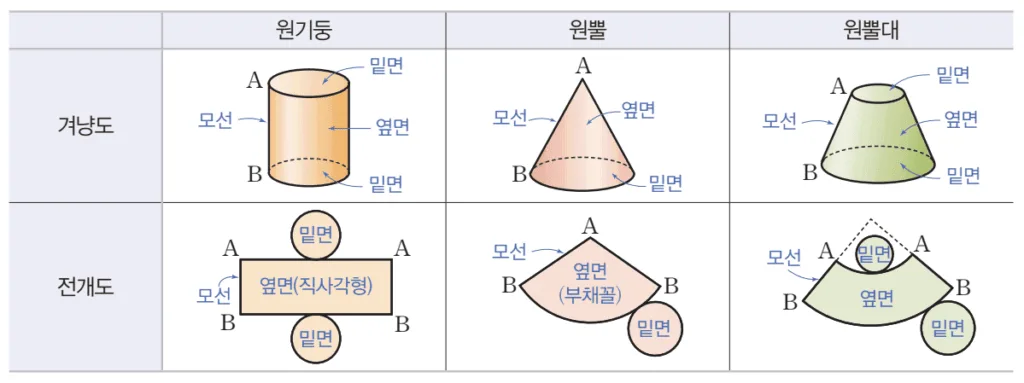
원기둥의 전개도
- 밑면 : 합동인 두 원
- 옆면 : 직사각형
- $\overset{\mmlToken{mo}{⏜}}{AA’}$ : 밑면의 둘레
- $\overline{AB}$ : 원기둥의 높이, 모선의 길이
원뿔의 전개도
- 밑면 : 하나의 원
- 옆면 : 부채꼴
- $\overline{AB}$ : 원뿔의 모선의 길이, 부채꼴의 반지름
- $\overset{\mmlToken{mo}{⏜}}{BB’}$ : 밑면의 둘레
원뿔대 전개도
- 밑면 : 두 원(작은원, 큰원)
- 옆면 : 큰 부채꼴에서 작은 부채꼴 제외한 영역
- $\overset{\mmlToken{mo}{⏜}}{AA’}$ : 작은 밑면의 둘레
- $\overset{\mmlToken{mo}{⏜}}{BB’}$ : 큰 밑면의 둘레
- $\overline{AB}$ : 모선의 길이, 두 부채꼴의 반지름 차이
이상으로 회전체에 대한 이론을 마무리 하도록 하겠습니다.