원 안의 현이 가진 성질은 중학교 수학에서 자주 등장하는 개념 중 하나입니다. 하지만 “왜 그런가?”에 대해 고민하지 않고 단순히 외우는 데 그치는 경우가 많습니다. 이번 시간에는 ‘현의 성질’이 왜 성립하는지, 그 논리적 이유를 이등변삼각형의 성질을 통해 직접 증명해 보려 합니다.
나아가 증명 과정에서 우리가 흔히 빠지는 순환논리의 오류에 대해서도 살펴보고 그 오류를 피하기 위한 중요한 수학적 도구인 귀류법을 실제 문제에 적용해 보면서, 어떻게 하면 더 정확하고 설득력 있게 수학을 설명할 수 있는지도 배워보겠습니다.
목차
학습목표
현과 두 반지름이 이루는 도형은 이등변삼각형이 된다. 이를 이용하여 현의 기본적인 성질을 증명하고, 학생들이 자주 범하는 오류에 대해 살펴보기로 하자.
- 직각 삼각형의 합동조건을 이용해 현의 성질을 논리적으로 설명할 수 있다.
현의 성질(기본)
중심이 $O$인 원과 원위의 점 $A, B$에 대하여 다음이 성립한다.
- $O$에서 현 $AB$에 내린 수선은 현을 수직이등분 한다.
- 현$AB$의 수직이등분선은 $O$를 지난다.
$\triangle{OAB}$는 $\overline{OA}=\overline{OB}$ 인 이등변 삼각형이다. 따라서 이등변삼각형의 성질을 이용하면 아래와 같은 결과를 이끌어 낼 수 있다. 증명과정은 이등변삼각형의 성질에서 이미 다루었으므로 여기서는 두 번째에 대한 증명만 다루기로 하자.
증명
순환논리의 오류
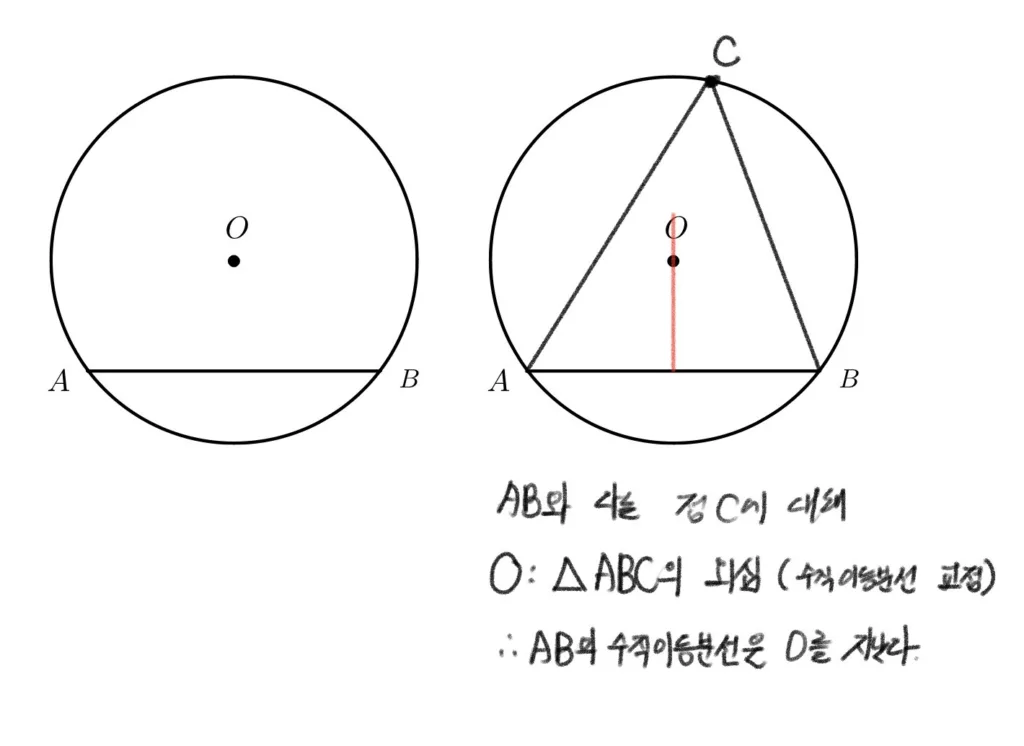
위의 증명은 현$AB$의 수직이등분선이 $O$를 지나는 것을 외심을 이용해 보이는 과정을 서술한 것이다. 무엇이 잘못되었을까? 현$AB$의 수직이등분선이 $O$를 지나는지를 물어보는 질문에 수직이등분선의 교점이 외심$O$ 이니까 맞다 라는 논리를 전개하고 있다. 이는 증명하라는 결론을 증명과정에 가져다 써놓고서 맞으니까 맞다는 식의 억지주장이다.
이와 같이 결론 자체를 맞다고 생각하고 이를 논증의 전제로 사용하고 결론이 맞다고 주장하는 것을 순환논리라고 한다. 이해를 돕기위해 언어적인 예시를 들어 살펴보자.
- 나는 거짓말을 안하니까 내 말은 다 맞는 말이야.
- 옳은 일을 해야 한다. 왜냐면 그게 옳기 때문이다.
이와 같은 논리로 말하거나 논증하는 것은 절대로 안될 일이다. 수학이든 현실에서든 논리적으로 생각하면서 살아간다면 이런 오류를 줄일 수 있을것이다.
올바른 증명
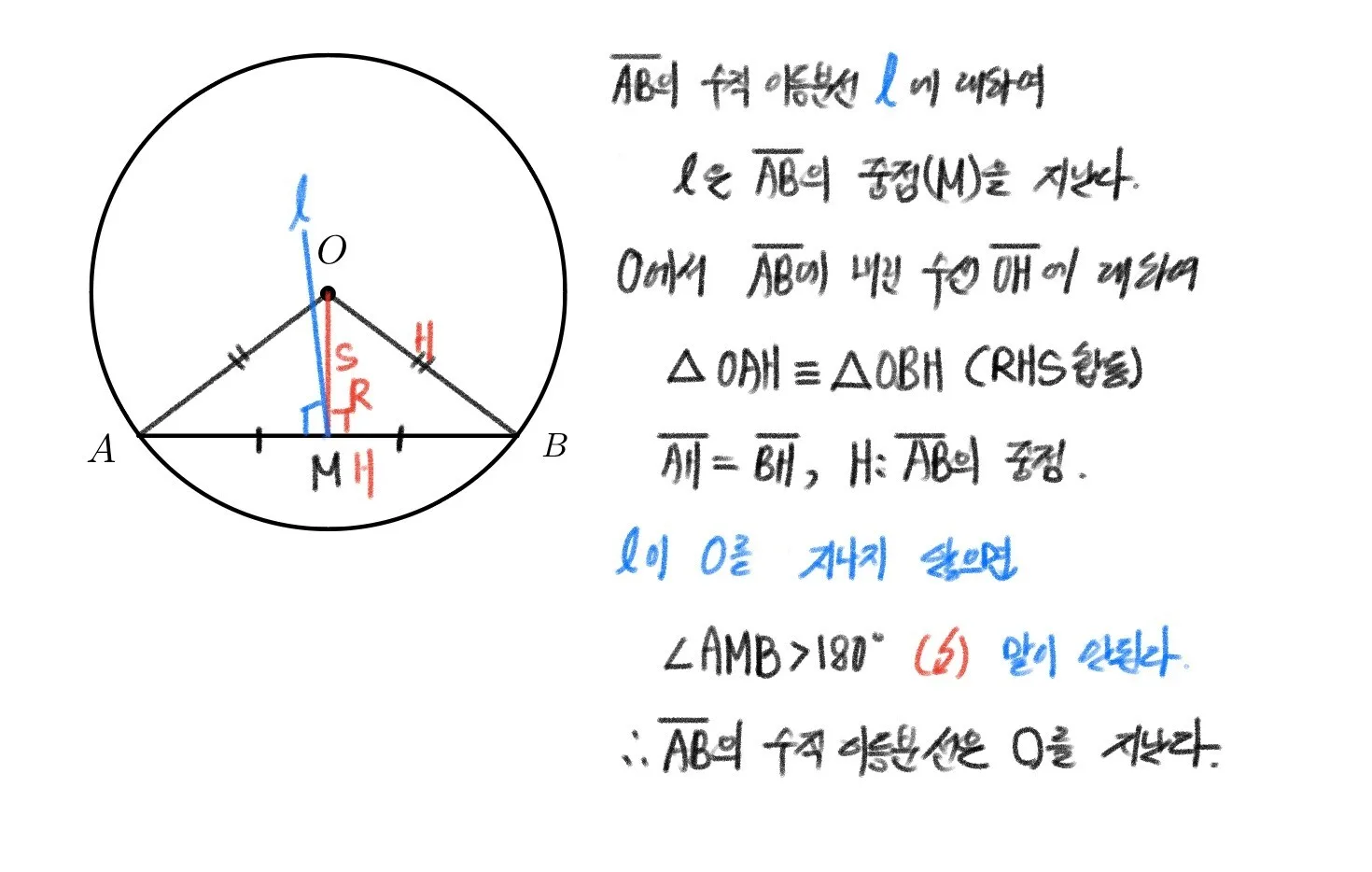
‘현 $AB$의 수직이등분선은 $O$를 지난다.’를 증명하려고 하니 너무 당연해 무엇을 증명할지 막막할 것이다. 이런 상황에서 결론을 부정 하여 조건으로 사용하는 귀류법을 이용해야 한다. 이 문제는 이전의 이등변삼각형의 귀류법 증면과 거의 유사한 상황이다. 이 문제 상황에 맞춰 논리적으로 다시 서술하여 정리하자.
현의 성질
기본적인 현의 성질을 학습했으니 이를 이용해 다음의 현의 성질을 학습해 보자.
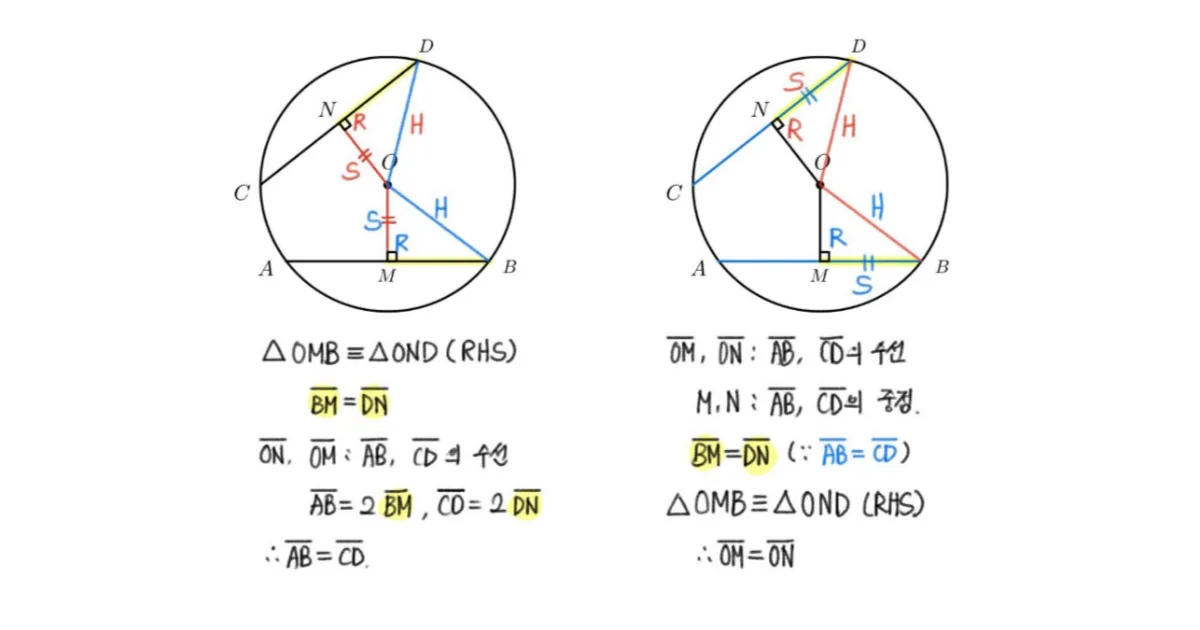
원 $O$ 위의 네 점 $A, B, C, D$에 대하여 다음이 성립한다.
- $\overline{OM}=\overline{ON}$ 이면 $\overline{AB}=\overline{CD}$
- $\overline{AB}=\overline{CD}$ 이면 $\overline{OM}=\overline{ON}$
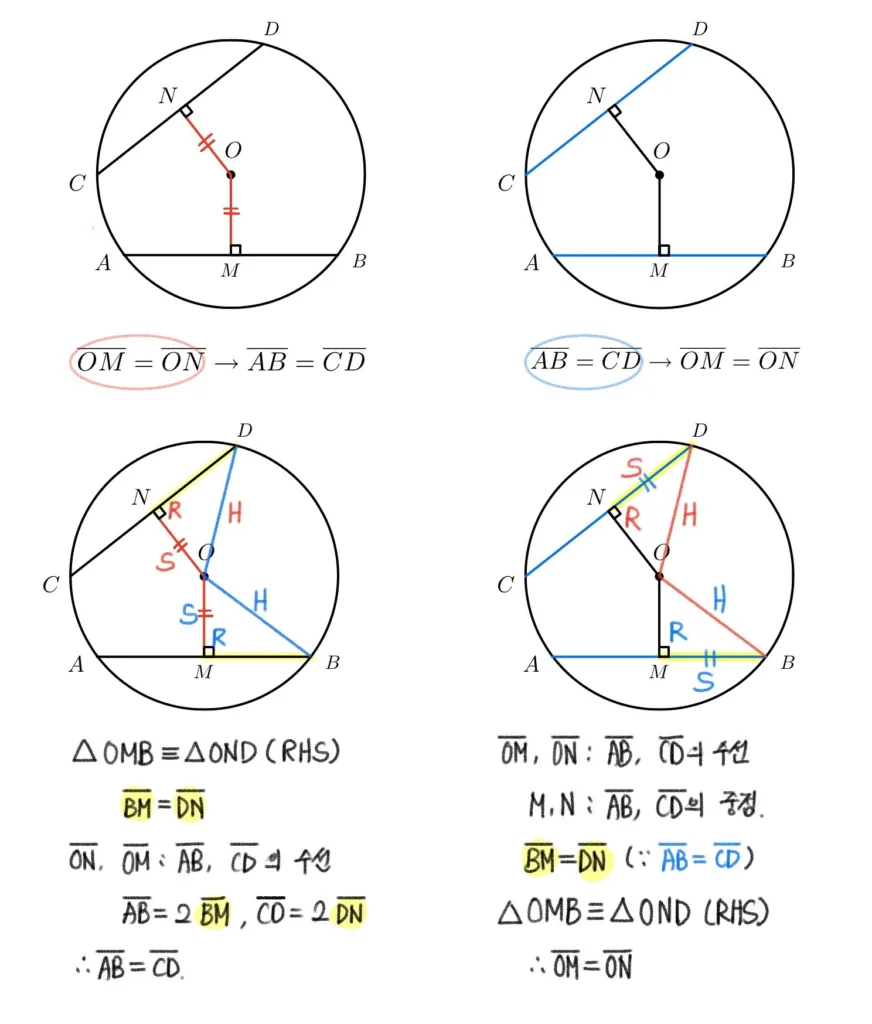
이와 같이 양쪽 방향이 모두 성립(참)하는 경우에 두 개의 문장을 동치라 하고 수식으로 다음과 같이 표현한다.
- $\overline{OM}=\overline{ON}\Leftrightarrow\overline{AB}=\overline{CD}$
위에서 증명한 현의 성질을 그림으로 도식화하여 정리하면 다음과 같다.
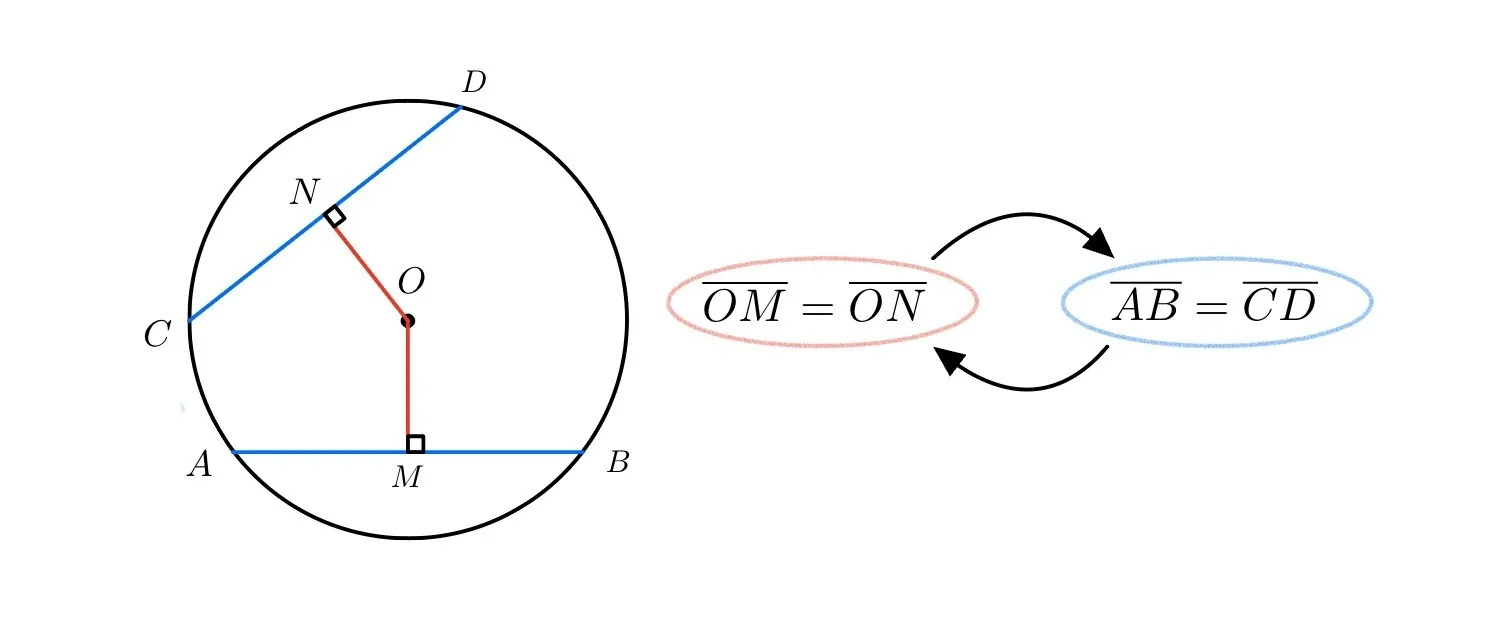
정리
이번 시간에는 현의 성질에 대한 내용을 학습하였다. 논증의 과정에서 자주 발생하는 순환논리의 오류에대하여 새롭게 학습하였다. 현실에서는 말도 안되는 논리이지만 수학을 풀다보면 자신의 생각에 심취하여 아주 빈번하게 범하는 오류이다. 수학을 더욱 재미있게 학습하려면 이런 사소한 부분의 생각을 정리하는 과정에 더 집중해 보길 바란다.
이번 시간에 배운 내용을 간단히 정리하면 아래와 같다.
- 현의 기본 성질
- $O$에서 현 $AB$에 내린 수선은 현을 수직이등분 한다.
- 현$AB$의 수직이등분선은 $O$를 지난다.
- 중심과 현사이의 거리와 현의 길이
- 현의 길이가 같으면 중심과 현 사이의 거리가 같다.
- 중심과 현사이의 거리가 같으면 현의 길이가 같다.