삼각형의 세 변의 길이만으로 넓이를 구할 수 있는 방법이 있습니다. 바로 헤론의 공식인데, 이 공식은 단순한 계산 도구를 넘어 내접원과 방접원, 접선의 길이, 닮은 삼각형의 개념이 함께 얽혀 있는 흥미로운 수학적 결과입니다. 이번 글에서는 헤론의 공식을 유도하는 과정을 따라가며 이와 관련된 개념들을 하나씩 정리하고, 이를 실제 문제에 어떻게 적용할 수 있는지를 알아보겠습니다.
도형을 많이 그려야 하기 때문에 바로 아래 링크에서 학습지를 다운받아 사용하는 것을 추천합니다.
목차
학습목표
접선의 길이와 관련된 내용을 내접원과 방접원에 적용하여 정리하고 나아가 내접원의 반지름을 구하고, 삼각형의 넓이를 구하는 과정까지 살펴보기로 하자.
- 헤론의 공식을 유도하는 과정을 학습하면서 내접원과 방접원이 주어진 문제에서 접선의 길이에 대한 성질을 완벽하게 설명 할 수 있다.
선행지식(복습)
내접원과 방접원
내용을 학습하기 앞서 내접원과 방접원에 관한 정리를 하고 시작하겠습니다.
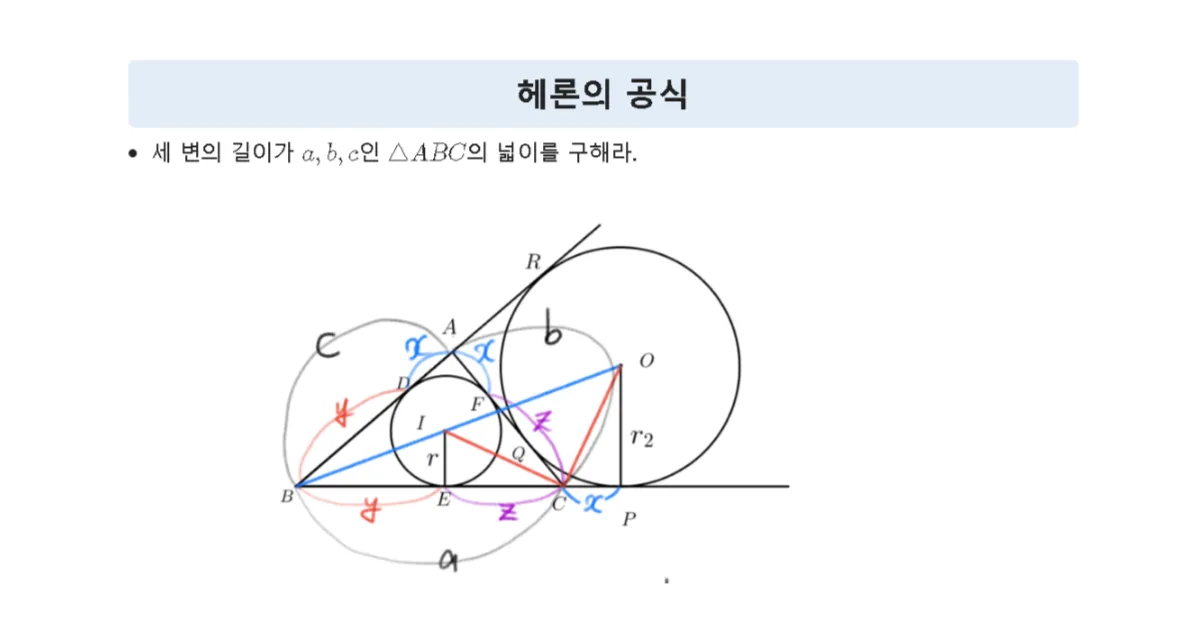
- 삼각형 $\triangle{ABC}$의 세 변의 직선에 동시에 접하는 원은 정확히 4개 존재한다. 한 원은 세 변의 내부의 세 변과 접하며, 이를 삼각형 $\triangle{ABC}$의 내접원이라 한다. 나머지 세 원은 삼각형의 한 변과 나머지 두 변의 연장선과 동시에 접하고 이를 삼각형 $\triangle{ABC}$의 방접원 이라고 합니다.

접선의 성질
이 내용을 이해하기 위해서는 접선의 성질에 대해 학습한 내용을 알아야 한다. 복습이 필요한 학생은 아래 링크를 참고하여 학습하시길 바랍니다.
접선의 길이 문제 풀이
방접원과 접선의 길이
- 주어진 삼각형 $\triangle{ABC}$과 방접원의 중심(방심) $O$에 대하여 $\overline{BP}$의 길이를 구하여라.

이 문제를 해결한 후 주목해야 할 사실은 다음과 같다.
- $[\triangle{ABC}의 둘레]=2\overline{BP}=2\overline{BR}$
내접원과 접선의 길이
- 주어진 삼각형 $\triangle{ABC}$와 내접원 $I$에 대하여 원 밖의 세 점 $A, B, C$에서 내접원에 그 은 접선의 길이를 모두 구하여라.

이로부터 다음과 같은 사실을 알 수 있다.
- $[\triangle{ABC}의 둘레]=2(x+y+z)$
내접원과 방접원의 접선의 길이 정리
내접원과 방접원의 접선의 길이는 삼각형의 둘레와 밀접한 관련이 있음을 알 수 있었다. 이를 다시 정리하면 다음과 같은 결론을 얻을 수 있다.
- $[\triangle{ABC}의 둘레] =2\overline{BP}=2\overline{BR}$
- $[\triangle{ABC}의 둘레] =2(x+y+z)$
- $\overline{BP}=\overline{BR}=x+y+z$
내접원과 방접원의 접선의 길이 응용
- 삼각형 $\triangle{ABC}$과 내접원 $I$, 방접원 $O$의 접점 $D, E, F, P, Q, R$에 대하여 $\overline{AD}=\overline{AF}=x$, $\overline{BD}=\overline{BE}=y$, $\overline{CE}=\overline{CF}=z$ 일 때 다음을 보여라.
- $\overline{AR}=\overline{CE}=z$
- $\overline{CP}=\overline{AD}=x$
- $\overline{DR}=\overline{EP}=x+z$
- $\overline{FQ}=z-x$

내접원의 반지름, 삼각형의 넓이
- 삼각형 $\triangle{ABC}$, 내접원 $I$, 방접원 $O$의 반지름 $r, r_2$와 접점 $D, E, F, P, Q, R$에 대하여 $\overline{AD}=\overline{AF}=1$, $\overline{BD}=\overline{BE}=5$, $\overline{CE}=\overline{CF}=3$ 이라 할 때, $\triangle{BIE}\sm\triangle{BOP}$ , $\triangle{IEC}\sm\triangle{CPO}$ 임을 보이고, 이를 이용하여 내접원의 반지름 $r$과 $\triangle{ABC}$의 넓이를 구해라.

이 문제의 풀이를 통해 기억해할 것은 바로 다음과 같다.
- 내접원과 방접원의 중식 $I, O$는 $\angle{B}$의 이등분선 상에 있다.
- $\triangle{BIE}\sm\triangle{BOP}$
- $\triangle{IEC}\sm\triangle{CPO}$
위의 내용을 일반적인 방법으로 정리하면 다음과 같은 헤론의 공식을 유도할 수 있다.
헤론의 공식
- 세 변의 길이가 $a, b, c$인 $\triangle{ABC}$의 넓이를 구해라.

마지막 박스 부분은 $x, y, z$에 대한 식을 세 변의 길이 $a, b, c$와 삼각형의 둘레 $s$로 정리하는 과정이다. 마지막에 도출된 식을 헤론의 공식이라고 한다.
정리(헤론의 공식)
헤론의 공식을 증명하고 이를 통해 세 변의 길이가 주어진 삼각형의 넓이를 구하는 방법을 학습하였고, 이 과정에서 내접원과 방접원의 개념, 접선의 길이에 대한 성질, 닮은 삼각형을 활용한 내접원의 반지름과 삼각형 넓이 계산방법을 부수적으로 정리하였다. 마지막의 헤론의 공식 유도는 중학교 수준에서 이해하기 어려운 내용이므로 심화 학습을 원하는 학생들만 학습하길 바랍니다.
세 변의 길이가 $a, b, c$인 $\triangle{ABC}$의 둘레 $s=a+b+c$에 대하여 $\triangle{ABC}$의 면적
- $\triangle{ABC}=\sqrt{\frac{s}{2}(\frac{s}{2}-a)(\frac{s}{2}-b)(\frac{s}{2}-c)}$